




仅给出由式(4-17)求解 K 和 P 的算法。由式(4-18)求解 K 和 P 的算法与之类似。
首先选择一适当的 γ 满足0< γ <1,解下面的关于未知矩阵 Q 和 W 的矩阵不等式
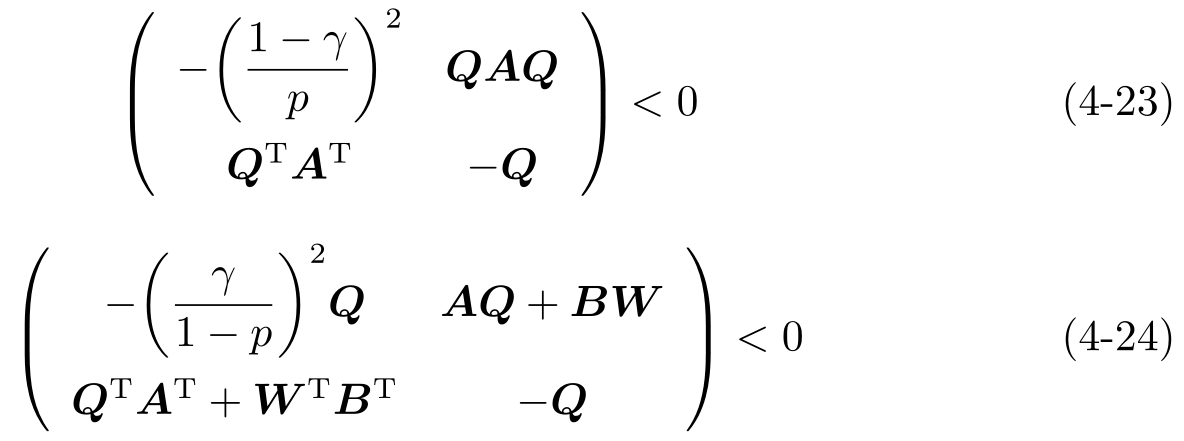
得到 K = W Q -1 ,利用Cholesky分解,由 Q = P -1 P -T 可获得 P 。
对上面的算法做一些说明。
利用 K = W Q -1 和 Q = P -1 P -T ,式(4-23)和式(4-24)可分别写为
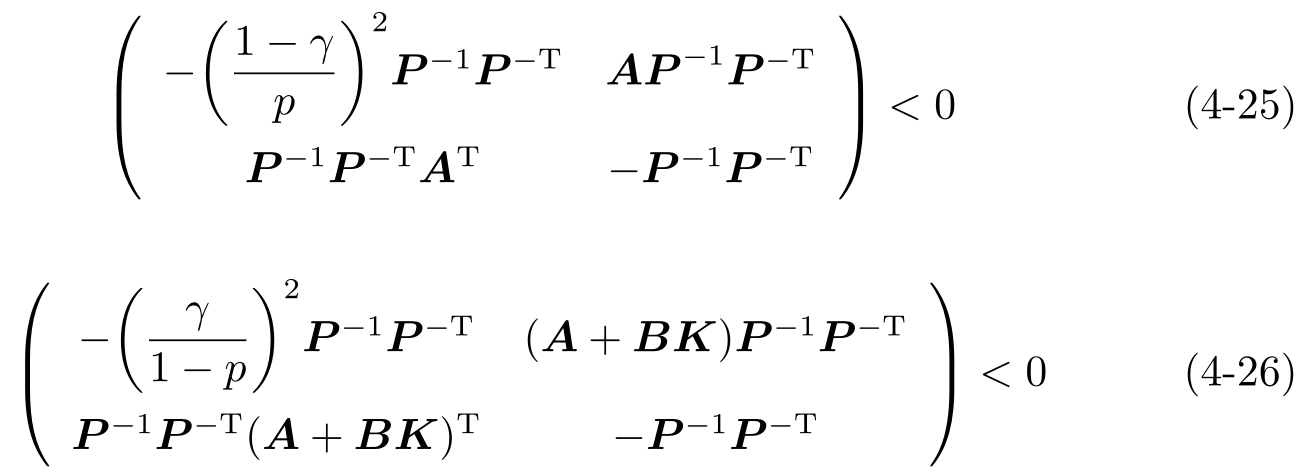
分别用diag[ P , I ]和它的转置左乘和右乘式(4-25)和式(4-26),可得
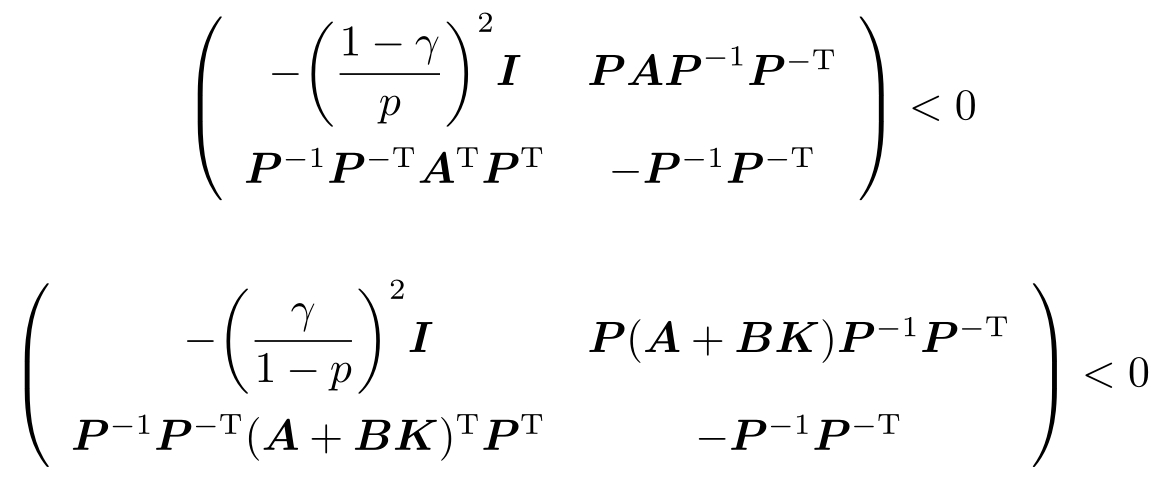
由Schur补引理,得到
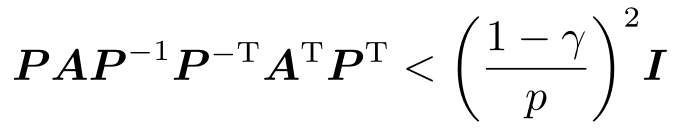
和
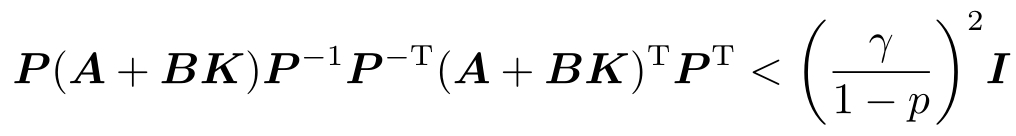
这蕴含
δ ( P AP -1 ) p <1 -γ
和
δ ( P ( A + BK ) P -1 )(1 -p )< γ
这样就有了式(4-17)。