




基于上述编码方案,下面给出关于闭环系统平均渐进稳定和几乎处处渐进稳定的结果。
采用状态反馈控制器
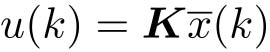 ,见式(4-3)~式(4-5)。控制器接收的状态估计
,见式(4-3)~式(4-5)。控制器接收的状态估计
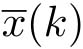 可以写成
可以写成
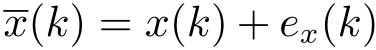 ,其中
e
x
(
k
)是量化误差。这样闭环系统变为
,其中
e
x
(
k
)是量化误差。这样闭环系统变为
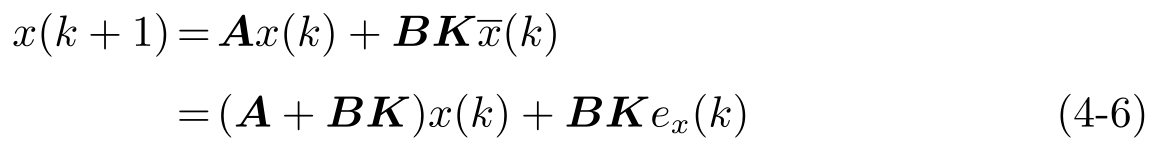
引理4.1 定义
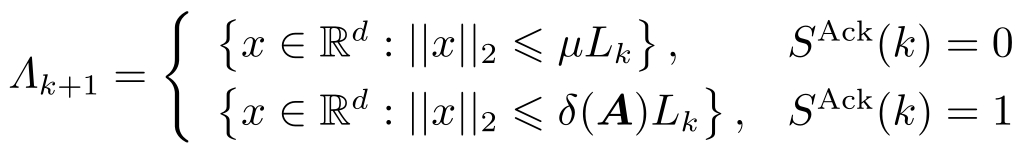
如果
x
(
k
)∈
Λ
k
,则
x
(
k
+1)∈
Λ
k
+1
。这里
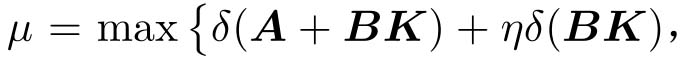
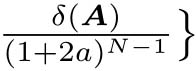 ,
,
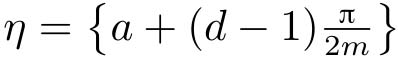 (见定理2.1),
δ
(·)表示矩阵的最大奇异值。
(见定理2.1),
δ
(·)表示矩阵的最大奇异值。
证明: 首先,令 S Ack ( k )=0。如果 x ( k )∈ S N ( k )\ S 1 ( k ),由定理2.1,有
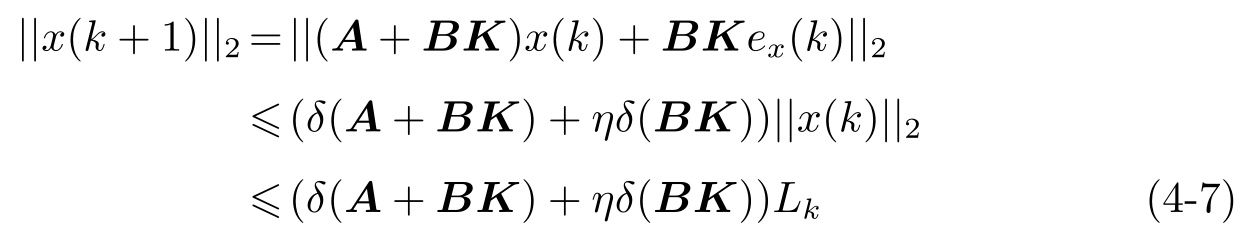
如果
x
(
k
)∈
S
1
(
k
),则
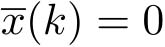 且
且
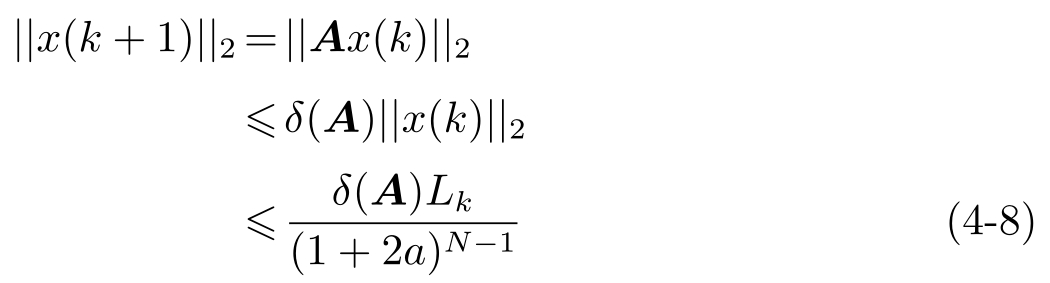
因此,由式(4-7)和式(4-8),有
|| x || 2 ≤ µL k
其次,令
S
Ack
(
k
)=1。在这种情况下,有
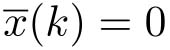 ,注意到
x
(
k
)∈
Λ
k
,因此
,注意到
x
(
k
)∈
Λ
k
,因此
|| x ( k +1)|| 2 ≤ δ ( A )|| x ( k )|| 2 ≤ δ ( A ) L k
由该引理,可以根据
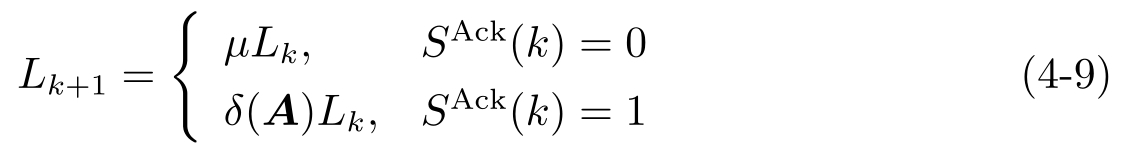
更新量化器( L k +1 , N,a,M )的参数 L k +1 。
定理4.1 如果量化器的参数( L k ,N,a,M )和增益矩阵 K 满足式(4-9)和

则具有噪声信道的系统式(4-1)是平均渐进稳定的。
证明: 证明分两部分。
(1)原点0∈R
d
是平衡点。令
x
(0)=0,由于
x
(0)∈
S
1
(0),根据编码方案,无论信道是否有擦除发生,都有
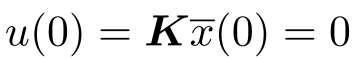 ,因此有
,因此有
x (1)= A x (0)=0
继续这一过程,可得到 x ( k )=0, k =2,3,4,…。
(2) E (|| x k || 2 )收敛到0。由式(4-9),有条件期望
E ( L k +1 | L k )= µL k (1 -p )+ δ ( A ) L k p
两边取条件期望,可得
E ( L k +1 )= E ( E ( L k +1 | L k ))
=( µ (1 -p )+ δ ( A ) p ) E ( L k )
因此 E ( L k )=( µ (1 -p )+ δ ( A ) p ) k E ( L 0 )。由式(4-10),则 k →∞, E ( L k )→0。由于|| x ( k )|| 2 ≤ L k ,因此当 k →∞, E (|| x k || 2 )→0。
定理4.2 如果量化器( L k ,N,a,M )的参数和增益矩阵 K 满足式(4-9)和

则具有噪声信道的系统式(4-1)是几乎处处渐进稳定的。
证明: 仅需要证明 L k 几乎处处趋于0。
式(4-9)可以写为下面的随机差分方程
L k +1 = ∆ ( k ) L k
式中,随机变量
∆
(
k
)是独立同分布的,且其分布为
P
r
(
∆
(
k
)=
µ
)=1
-p
,
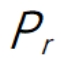 (
∆
(
k
)=
δ
(
A
))=
p
。由于
(
∆
(
k
)=
δ
(
A
))=
p
。由于
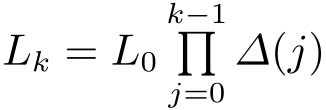 ,需要证明
,需要证明
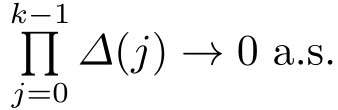 。其中,“a.s.”表示“几乎处处”。由大数定律,有
。其中,“a.s.”表示“几乎处处”。由大数定律,有
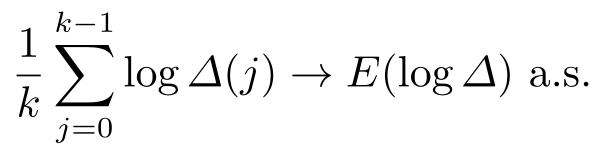
进一步,有
E (log ∆ )=(1 -p ) log µ + p log δ ( A )
=log( µ (1 -p ) [ δ ( A )] p )
这样,由式(4-11), E (log ∆ )<0成立,有
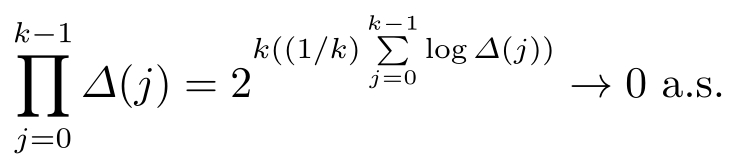
给定反馈矩阵 K ,即使 A + B K 的每个特征值的绝对值都小于1,即 A + B K 是Schur稳定的, δ ( A + B K )却可以大于1。这样不等式(4-10)和式(4-11)将没有解。为解决这一问题,可以利用引理3.1。
令
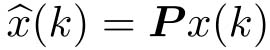 ,
,
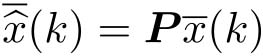 ,其中
P
是一个可逆矩阵。由式(4-6),有
,其中
P
是一个可逆矩阵。由式(4-6),有
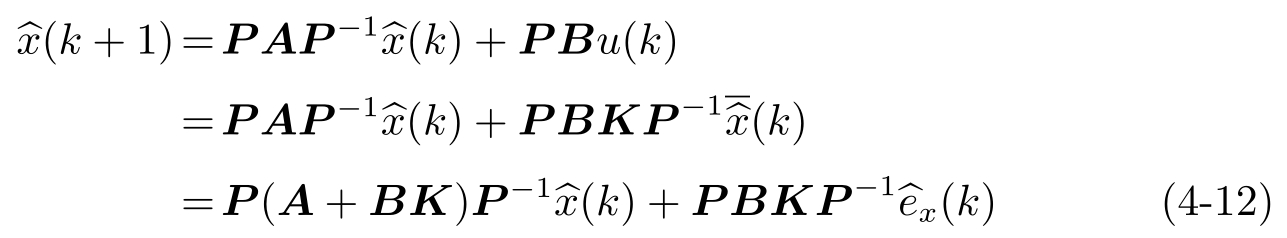
其中,
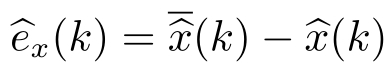 。
。
推论4.1 如果量化器( L k ,N,a,M )的参数和反馈矩阵 K 满足
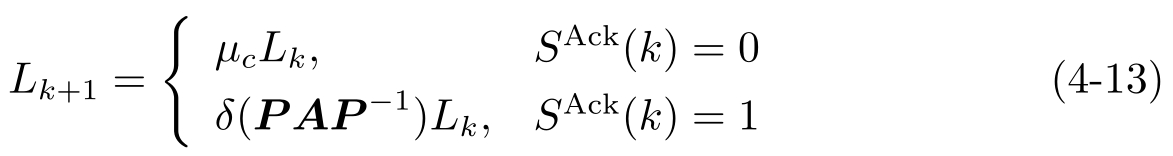
和
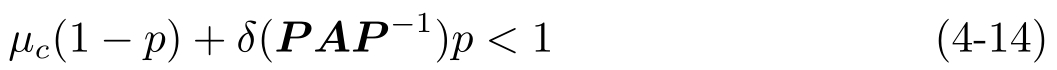
这里
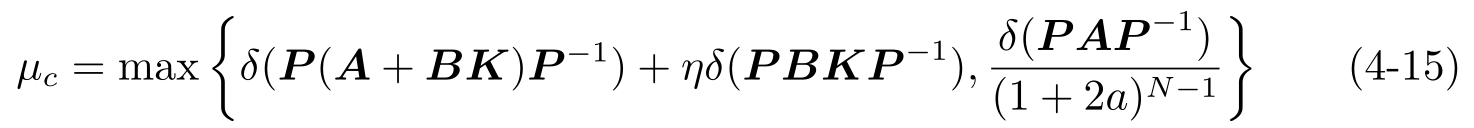
则具有噪声信道的闭环系统式(4-12)是平均渐进稳定的。
推论4.2 如果量化器( L k ,N,a,M )的参数和反馈矩阵 K 满足式(4-13)和

则具有噪声信道的闭环系统式(4-12)是几乎处处渐进稳定的。
现在给出问题4.1和问题4.2的解法如下。
(1)控制器设计:对于问题4.1,求解 K 和 P 使得
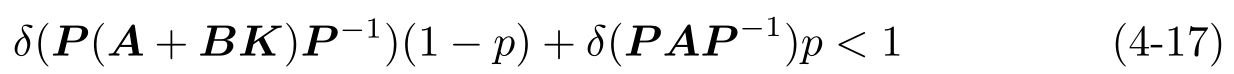
对于问题4.2,求解 K 和 P 使得
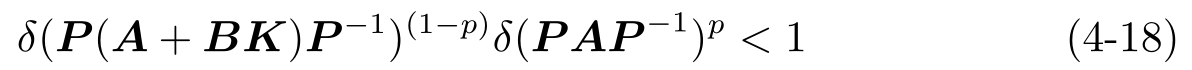
注意到如果 K 和 P 满足式(4-17)或式(4-18),那么 A + B K 是Schur稳定的。由式(4-17)或式(4-18)求解 K 和 P 的算法在4.4节中给出。
(2)量化器设计:对于问题4.1,获得 K 和 P 后,我们选择 a 和 M 使得
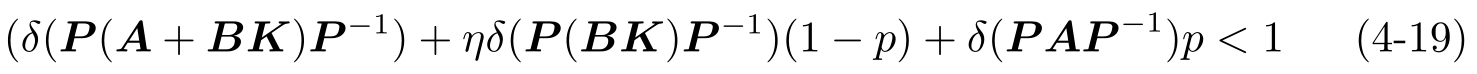
其中,
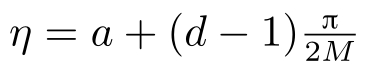 (见定理2.1)。
(见定理2.1)。
对于问题4.2,选择 a 和 M 使得
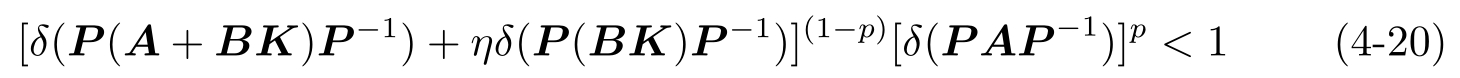
然后,选择 N 使得
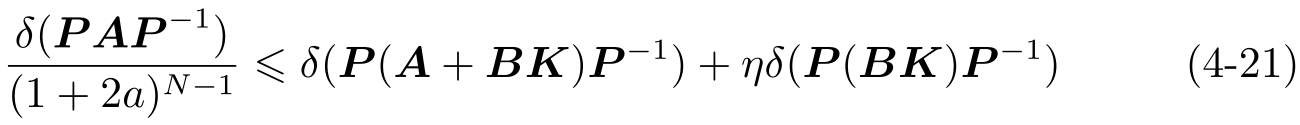
最后,根据式(4-13)和
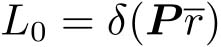
确定
L
k
。这里
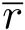 是初始状态
x
(0)的上界,见式(4-2)。
是初始状态
x
(0)的上界,见式(4-2)。
(3)编码器设计。
令 S Ack (-1)=0。
①接收状态信号
x
(
k
),将其变换为
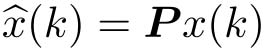 。
。
②利用量化器(
L
k
,N,a,M
)将
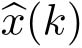 编码为
编码为
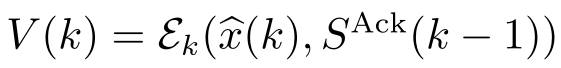 。
。
③发送 V ( k )给解码器,接收解码器的确认信号 S Ack ( k )。
④更新时间 k = k +1,返回第一步。
(4)解码器设计。
①在
k
时刻,如果没有擦除发生,设定
S
Ack
(
k
)=0,
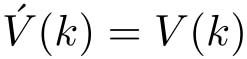 ;如果有擦除发生,设定
S
Ack
(
k
)=1,
;如果有擦除发生,设定
S
Ack
(
k
)=1,
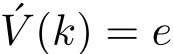 。
。
②将
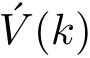 解码为
解码为
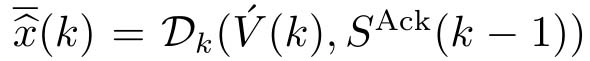 ,发送确认信号
S
Ack
(
k
)给编码器。
,发送确认信号
S
Ack
(
k
)给编码器。
③将
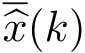 变换为
变换为
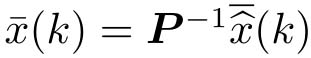 。
。
④更新时间 k = k +1,返回第一步。
为保证量化器可以工作,所需信道码率 R 应满足
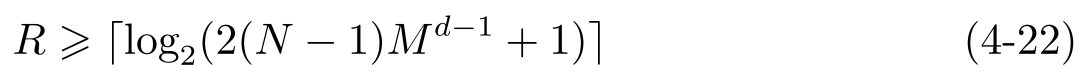
式中,
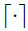 是Ceiling函数,即大于自变量的最小整数。
是Ceiling函数,即大于自变量的最小整数。
注解4.1
在式(4-14)和式(4-16)中,
η
是与信道性能有关的参数,见式(4-15)、式(4-21)和式(4-22)。另外,
µ
c
(1
-p
)+
δ
(
P AP
-1
)
p
和
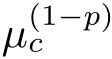 [
δ
(
P AP
-1
)]
p
描述与系统收敛速率有关的控制性能,见定理4.1和定理4.2的证明。因此,不等式(4-14)和式(4-16)在某种意义上显示系统控制性能和通信性能的折中。
[
δ
(
P AP
-1
)]
p
描述与系统收敛速率有关的控制性能,见定理4.1和定理4.2的证明。因此,不等式(4-14)和式(4-16)在某种意义上显示系统控制性能和通信性能的折中。
注解4.2 由式(4-14)和式(4-16)可以看出,当擦除概率 p = p 0 满足式(4-14)和式(4-16)时,则 p<p 0 也一定满足这两个不等式。因此,如果在擦除概率 p = p 0 的条件下设计量化器和控制器保证系统平均渐进稳定和几乎处处渐进稳定,则该量化器和控制器一定可在 p<p 0 时保证系统平均渐进稳定和几乎处处渐进稳定。