




考虑下面的离散线性时不变系统
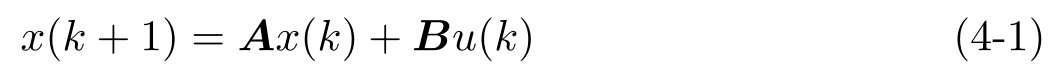
式中, x ( k )∈R d 和 u ( k )∈R m 分别是系统状态和输入, A 和 B 是适当维数的系统矩阵。不失一般性,假设 A 是不稳定的。与文献[11]一样,我们也假设初始状态 x (0)在一个有界区域内,即

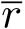 对编码器和解码器都是已知的。编码器对状态量
x
(
k
)编码,然后通过擦除信道发送到解码器。擦除信道的擦除概率为
p
。如文献[95]一样,假设解码器可反馈给编码器一个确认信号,以确认信道中擦除是否发生,因此编码器知道解码器收到什么信息。系统结构如图4-1所示。
对编码器和解码器都是已知的。编码器对状态量
x
(
k
)编码,然后通过擦除信道发送到解码器。擦除信道的擦除概率为
p
。如文献[95]一样,假设解码器可反馈给编码器一个确认信号,以确认信道中擦除是否发生,因此编码器知道解码器收到什么信息。系统结构如图4-1所示。
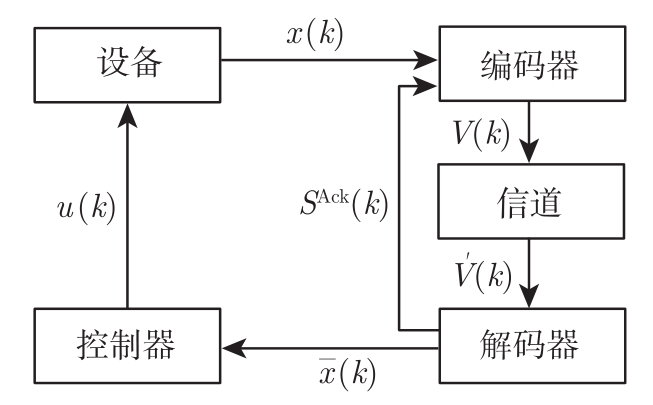
图4-1 系统结构
用 S Ack ( k )∈{0,1}表示在 k 时刻的确认信号,它由解码器发送,由编码器接收。进一步,定义随机变量

S Ack ( k )( k =0,1,2,3,…)是独立同分布的,其分布为: P r ( S Ack ( k )=0)=1 -p , P r ( S Ack ( k )=1)= p 。
(1)编码器: k 时刻的编码器是一个从( x ( k ), S Ack ( k -1))到 V ( k )∈ Σ 的映射 E k ,即
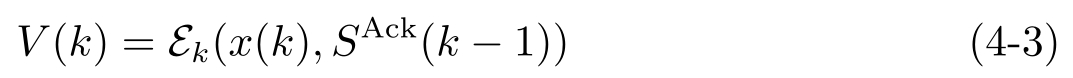
Σ 是码字的集合(码书)。注意:编码器不能获得控制输入。
(2)擦除信道:编码器在信道发送端发送
V
(
k
),受噪声等影响,在接收端变为
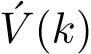 ,被解码器接收。擦除信道是无记忆的,并且满足概率条件
,被解码器接收。擦除信道是无记忆的,并且满足概率条件
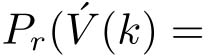 V
(
k
))=1
-p
,
V
(
k
))=1
-p
,
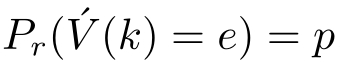 。这里
e
是擦除符号,表示擦除发生。
。这里
e
是擦除符号,表示擦除发生。
(3)解码器:
k
时刻的解码器是一个从
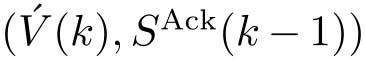 到
到
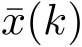 的映射
D
k
。其中
的映射
D
k
。其中
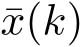 是
x
(
k
)的估计,即
是
x
(
k
)的估计,即
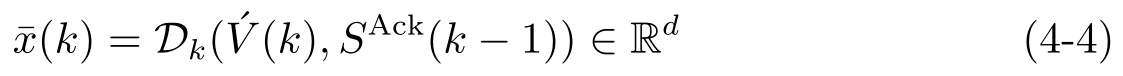
(4)控制器:控制器K是一个从
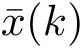 到
u
(
k
)∈R
m
的映射,即
到
u
(
k
)∈R
m
的映射,即

为简单起见,我们采用状态反馈控制器
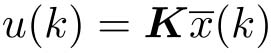 ,反馈增益矩阵为
K
。
,反馈增益矩阵为
K
。
定义4.1 具有噪声信道的系统式(4-1)是平均渐进稳定的,如果存在编码器、解码器和控制器使得对于由式(4-1)、式(4-3)~式(4-5)构成的闭环系统,原点0∈R d 是平衡点,且 E (|| x k || 2 )→0, k →∞。其中, E (·)表示数学期望。
定义4.2 具有噪声信道的系统式(4-1)是几乎处处渐进稳定的,如果存在编码器、解码器和控制器使得对于由式(4-1)、式(4-3)~式(4-5)构成的闭环系统,原点0∈R d 是平衡点,且当 k →∞,|| x k || 2 几乎处处趋于0。
在编码方案不使用控制信号的条件下,我们考虑的问题如下。
问题4.1 给定具有噪声信道的系统式(4-1),设计状态反馈矩阵 K 、球极坐标编码器{ E k ,k ≥0}和球极坐标解码器{ D k ,k ≥0}使得系统式(4-1)是平均渐进稳定的。
问题4.2 给定具有噪声信道的系统式(4-1),设计状态反馈矩阵 K 、球极坐标编码器{ E k ,k ≥0}和球极坐标解码器{ D k ,k ≥0}使得系统式(4-1)是几乎处处渐进稳定的。