下载掌阅APP，畅读海量书库
立即打开
现在给出球极坐标量化器的一个重要性质，利用这个性质可以简化系统稳定性的分析。先给出一个引理。
引理2.1
[
r θ
1
θ
2
…
θ
d
-2
θ
d
-1
]
T
和
分别表示
X
，
Y
∈R
d
的球极坐标，则有
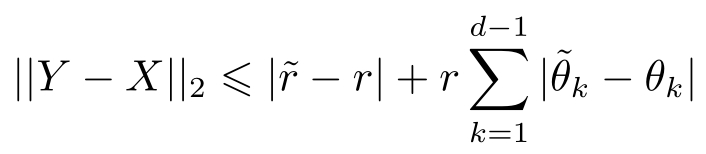
这里‖·‖ 2 表示向量的2范数。
证明： 用 d -1个球极坐标
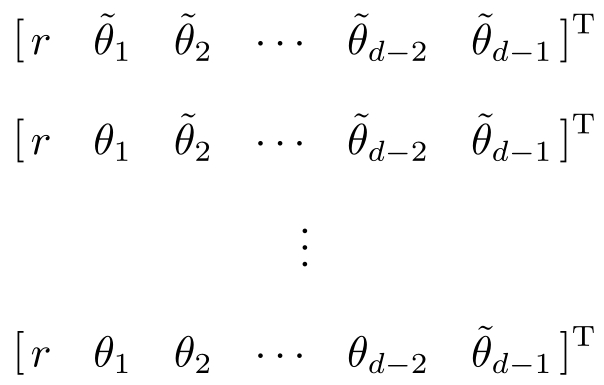
分别表示 d -1个点 Z 1 ， Z 2 ，…， Z d -1 ∈R d ，则有
|| Y-X || 2 ≤|| Y-Z 1 || 2 +|| Z 1 -Z 2 || 2 +…+|| Z d -2 -Z d -1 || 2 +|| Z d -1 -X || 2
并且
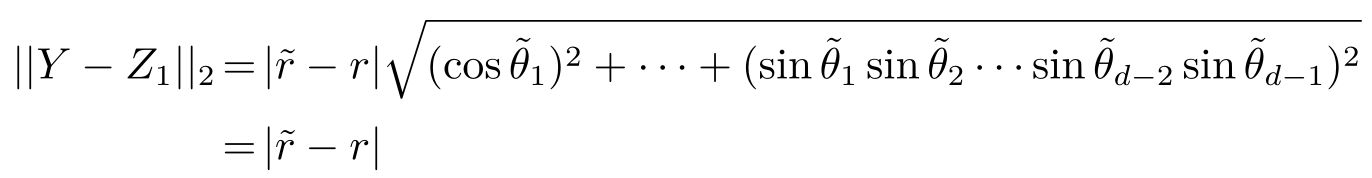
为估计|| Z 1 -Z 2 || 2 ，考虑连接点 Z 1 和 Z 2 的弧 γ ：
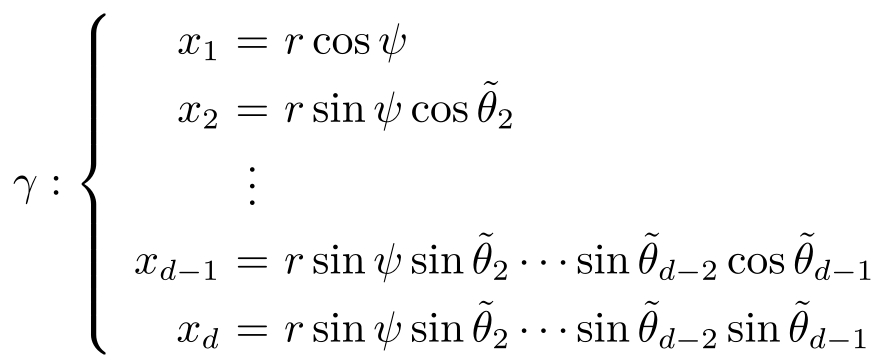
这里，参数
ψ
在
θ
1
和
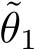之间变化。显然
|| Z 1 -Z 2 || 2 ≤length( γ )
进一步注意到
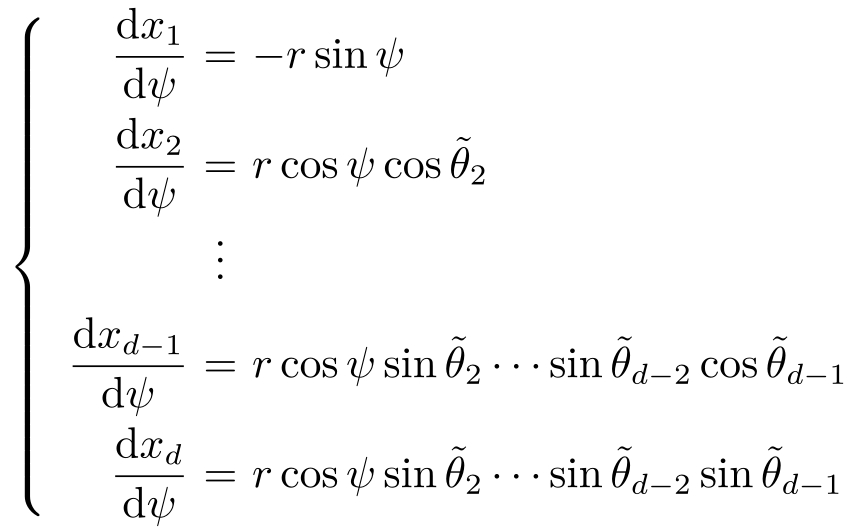
则有
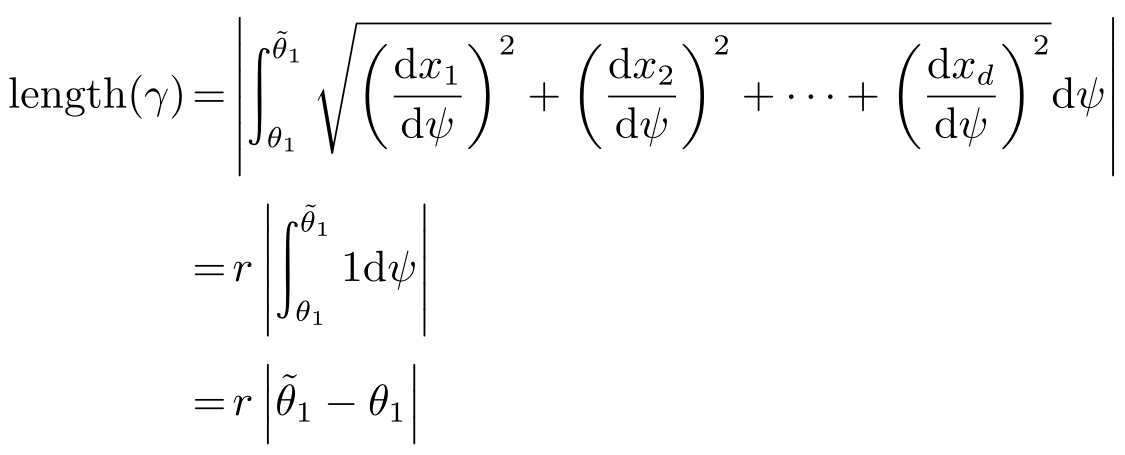
因此有
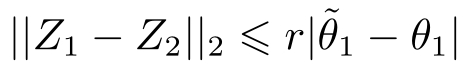
类似地，得到其他的估计，这样就完成证明。
图2-4为引理2.1的图示。
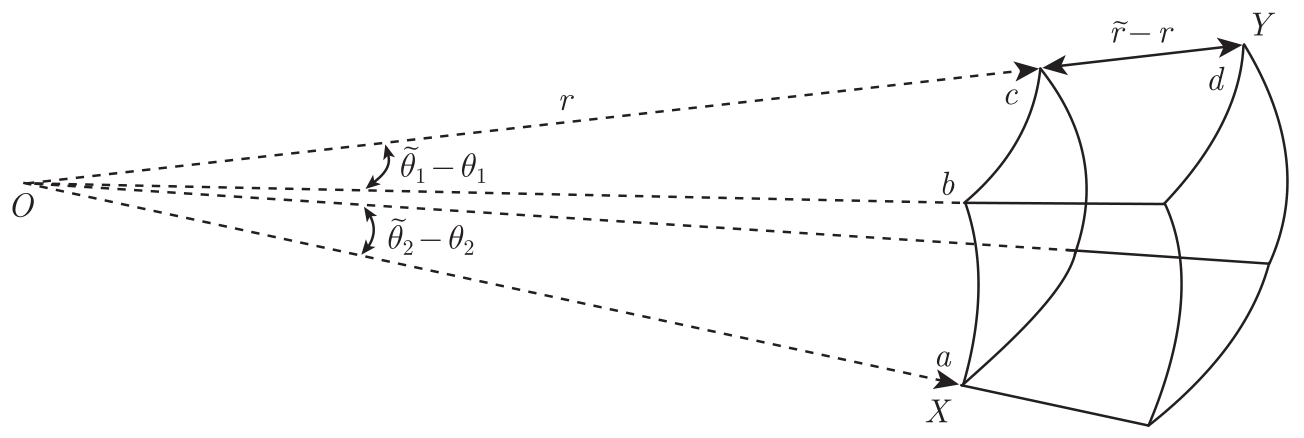
图2-4 引理2.1的图示
定理2.1 对于量化器（ L，N，a，M ）、编码映射 q 和解码映射 h ，任意的量化误差满足
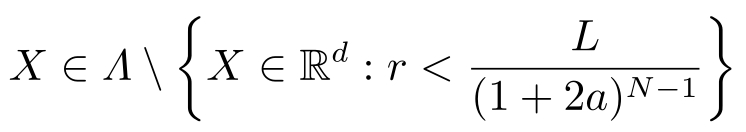
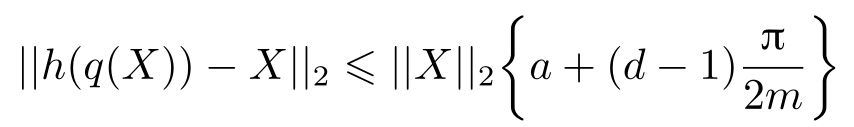
证明：
由于
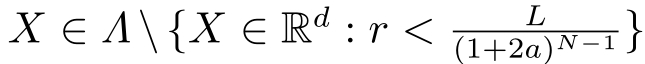，所以
X
位于由（
i，j
1
，
j
2
，…，
j
d
-2
，
s
）索引的量化块内（见定义2.1）。
X
的球极坐标[
r θ
1
θ
2
…
θ
d
-2
θ
d
-1
]
T
满足
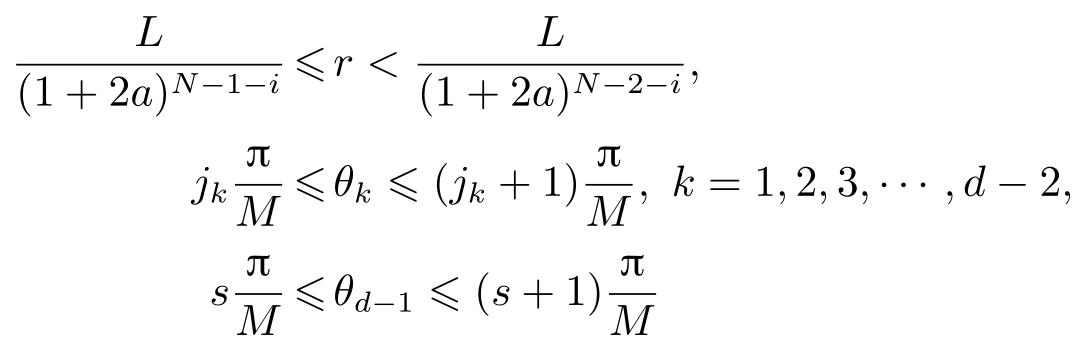
则 X 的量化值 h （ q （ X ））为
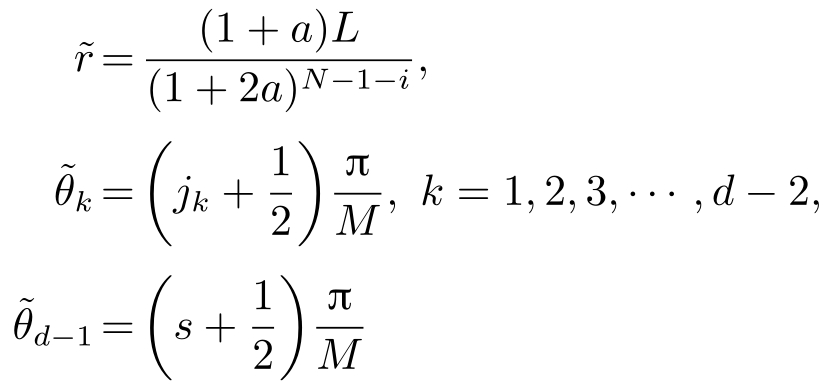
注意到 r =|| X || 2 ，由引理2.1可得
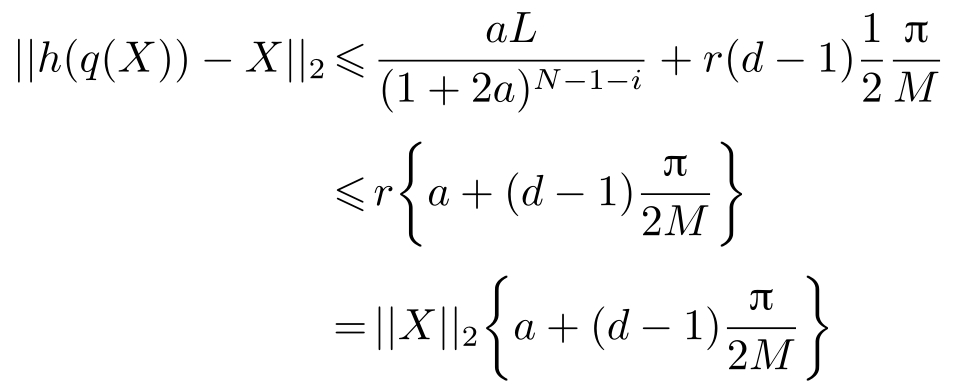
注解2.1
由定理2.1，在
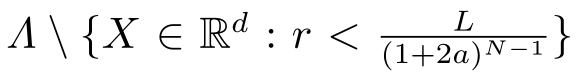中被量化的数据
X
和对应的量化误差
h
（
q
（
X
））
-X
之间的关系很自然地反映了一个直觉概念：当||
X
||
2
趋于0时，量化器的分辨率变得精细；反之，当||
X
||
2
远离0时，量化器的分辨率变得粗糙。
注解2.2 为获得有限码率，包含原点的最小球 S 1 （ k ）被看作一个量化块，不再被分割。