




对于笛卡儿坐标系中的向量 X =[ x 1 x 2 … x d -1 x d ] T ∈R d ,利用坐标变换
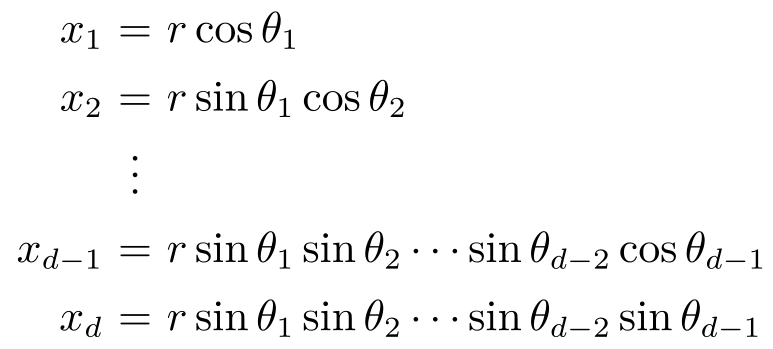
和

可以将其转换为球极坐标表达形式:
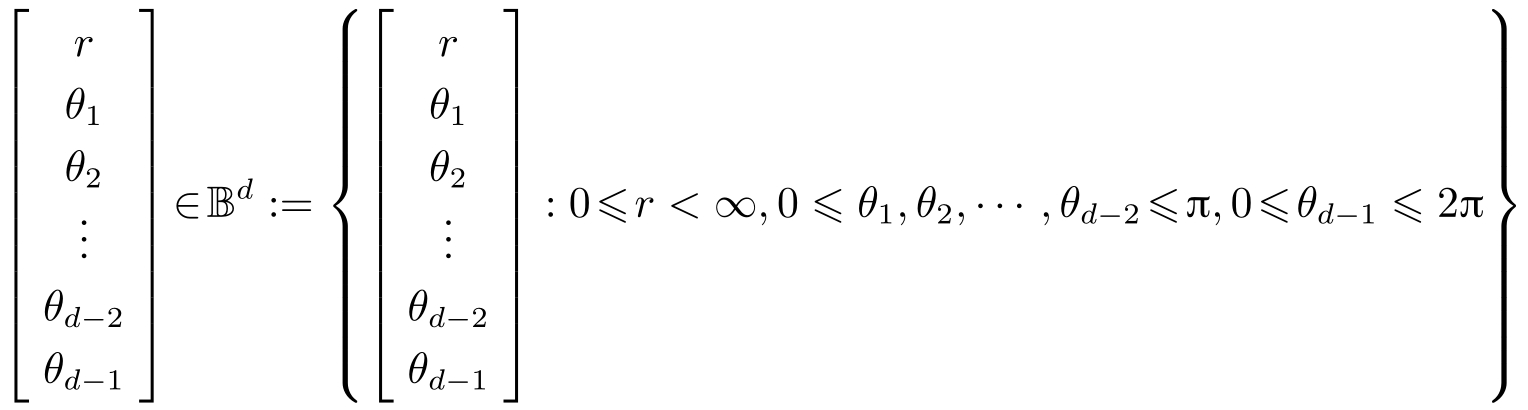
我们先给出球极坐标量化器的抽象定义,然后给出具体解释。
定义2.1 球极坐标量化器是一个四元组( L,N,a,M ),其中,实数 L >0表示支撑球的半径,正整数 N ≥2表示比例同心球的数目,实数 a >0表示比例系数,正整数 M ≥2表示将角弧度π平均分割的数目。量化器按如下方法将支撑球
Λ ={ X ∈R d : r<L }
分割为2( N -1) M d -1 +1个小的量化块。
(1)量化块集合
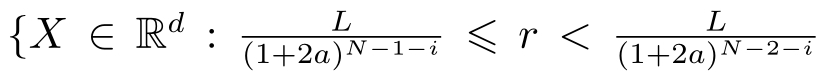 ,
,
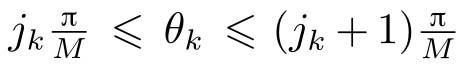 ,
k
=1,2,…,
d
-2,
,
k
=1,2,…,
d
-2,
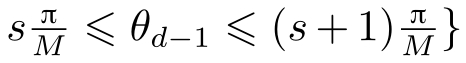 ,由(
i
,
,由(
i
,
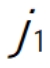 ,
,
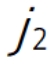 ,…,
,…,
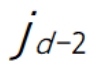 ,
s
)索引,其中,
i
=0,1,2,…,
N
-2;
j
k
=0,1,2,…,
M
-1;
k
=1,2,3,…,
d
-2。
s
=0,1,2,…,2
M
-1。量化块的数目为(
N
-1)·
M
d
-2
·2
M
=2(
N
-1)
M
d
-1
。
,
s
)索引,其中,
i
=0,1,2,…,
N
-2;
j
k
=0,1,2,…,
M
-1;
k
=1,2,3,…,
d
-2。
s
=0,1,2,…,2
M
-1。量化块的数目为(
N
-1)·
M
d
-2
·2
M
=2(
N
-1)
M
d
-1
。
(2)量化块
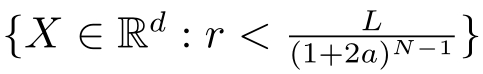 。
。
图2-3所示为二维球极坐标量化器。
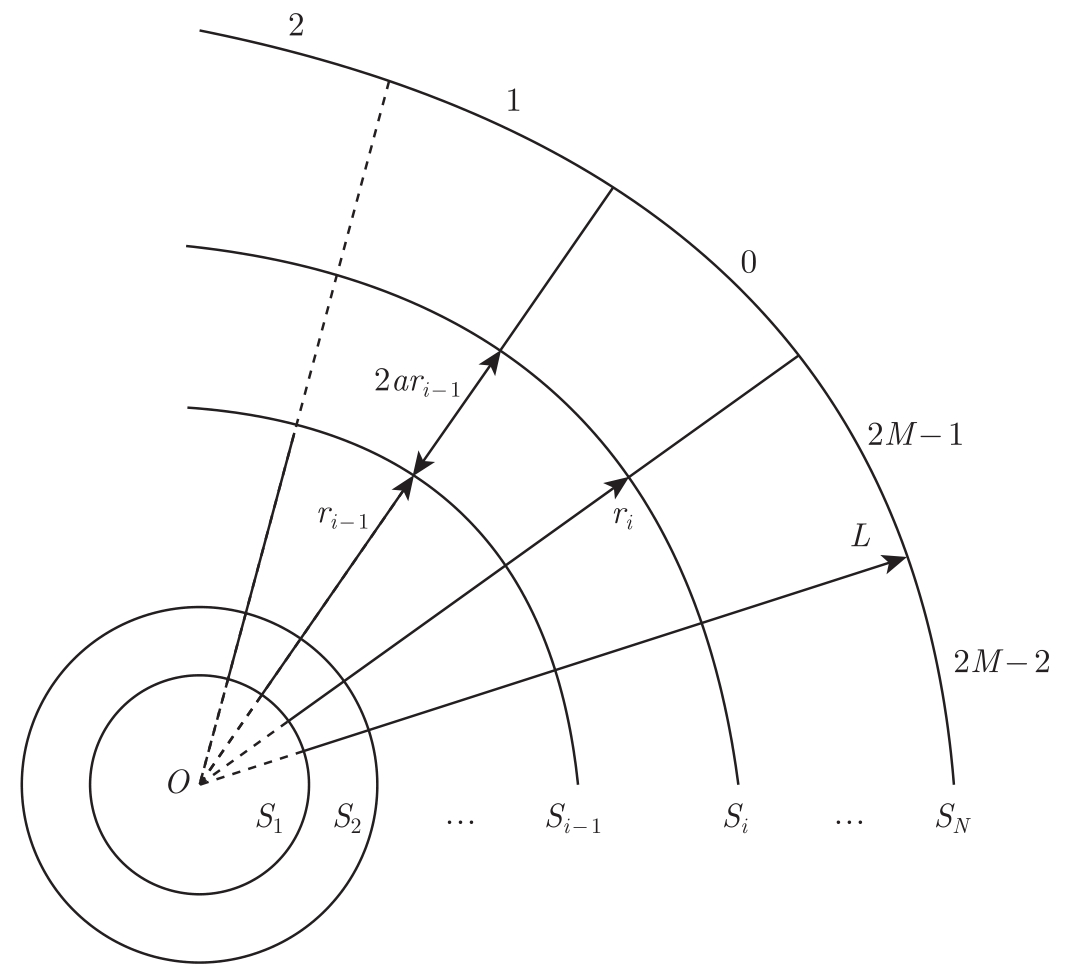
图2-3 二维球极坐标量化器
我们现在解释定义2.1的分割方法,对支撑球 Λ ={ X ∈R d : r<L }按下面步骤分割成2( N -1) M d -1 +1个小的量化块:
(1)先沿半径方向按比例分割支撑球。用 N 个同心球面 S i ( i =1,2,3,…, N ),沿半径 r 方向分割支撑球,同心球面 S i 的半径 r i 满足 r i / r i -1 =1+2 a ,即同心球半径成比例。最大球 S N 的半径 r N = L 。
(2)再沿 d -1个角度方向均匀分割支撑球。将角弧度π分割成 M 等份,将角弧度2π分割成2 M 等份。
(3)最里面包含原点的球
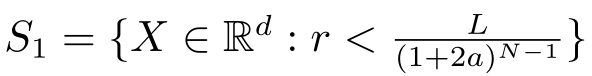 不再分割。
不再分割。
注意到0≤ θ 1 , θ 2 ,…, θ d -2 ≤π,0≤ θ d -1 ≤2π,这样支撑球 Λ 被分割成2( N -1) M d -1 +1个量化块。球极坐标量化器的参数 a 、 M 和 N 决定系统所需的信道码率,并影响系统稳定性。如何确定这些参数将在以后章节中具体介绍。
为获得球极坐标量化器的一个重要性质,下面我们定义编码映射和解码映射。对于量化器( L,N,a,M ), Σ 表示一个元素为2( N -1) M d -1 +1的集合,每个元素代表一个量化块。 Σ 也被称为码书。
定义2.2 映射
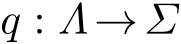 取
取
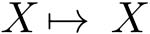 所在的量化块
σ
所在的量化块
σ
称为编码映射。对位于量化块边界上的点 X ,可按约定好的规则将其映射为码书 Σ 中的一个元素。
定义2.3 满足下面条件的映射
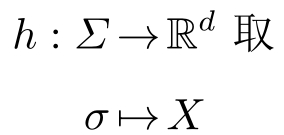
称为解码映射。
如果 σ 表示索引为( i,j 1 , j 2 , j 3 ,…, j d -2 , s )的量化块,其中, i =0,1,2,…, N -2; j k =0,1,2,…, M -1; k =1,2,3,…, d -2; s =0,1,2,…,2 M -1,则 h 将 σ 映射为 X , X 的球极坐标为
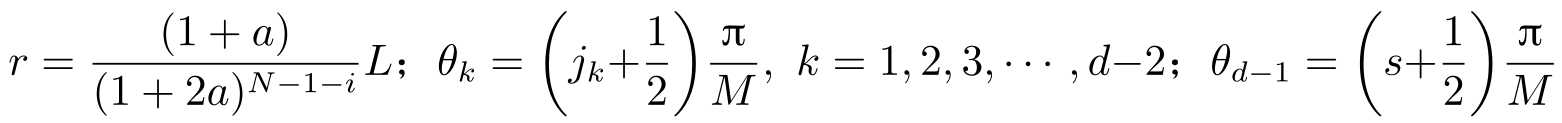
如果
σ
表示量化块
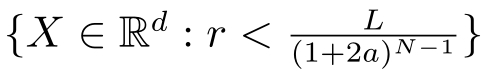 ,则
h
将
σ
映射为0∈R
d
。
,则
h
将
σ
映射为0∈R
d
。