




在量化控制领域中,目前文献广泛采用两种量化方法:均匀量化方法与对数量化方法。均匀量化方法是在笛卡儿坐标系中,将
N
维空间均匀分割成相同的小块(量化块)。当系统的状态或输出落入某个量化块时,以该量化块的中心(或块中某一点,根据实际需要而定)作为实际状态或输出的量化值,即用量化值代替实际值。量化值经网络传输,用于量化控制。图2-1所示为二维均匀量化器。均匀量化方法是比较简单的量化方法,被广泛使用
[19-20,26,47,67]
。在这种方法中,量化误差与实际值之间没有固定的关系。在图2-1中,
X
和
X
1
是系统实际状态,
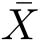 和
和
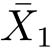 分别是
X
和
X
1
的量化值。在
X
和
分别是
X
和
X
1
的量化值。在
X
和
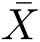 所在的量化块中,量化误差
e
X
的模与实际值
X
的模的比值
δ
X
为
所在的量化块中,量化误差
e
X
的模与实际值
X
的模的比值
δ
X
为
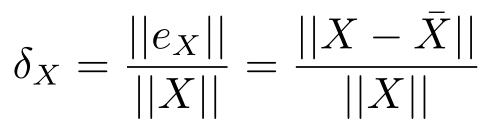
当
X
为
A
点时,比值
δ
X
=
δ
A
达到该量化块中的最大值。显然,对于不同的量化块,这个比值的最大值不同。例如,在
X
1
和
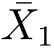 所在的量化块中,当
X
1
为原点
O
时,该比值无穷大。由于量化误差与实际值之间没有固定的关系(比值无界),因此不便于系统稳定性分析。另外,这种方案孤立地、分别地设计编码方案与控制器,而没有将编码方案设计与控制器设计很好地结合起来,这样就无法从整体上考虑系统的通信性能和控制性能。
所在的量化块中,当
X
1
为原点
O
时,该比值无穷大。由于量化误差与实际值之间没有固定的关系(比值无界),因此不便于系统稳定性分析。另外,这种方案孤立地、分别地设计编码方案与控制器,而没有将编码方案设计与控制器设计很好地结合起来,这样就无法从整体上考虑系统的通信性能和控制性能。
对数量化方法是Elia和Mitter提出的一种量化方法 [21] ,如图2-2所示为对数量化器。量化器将 v 轴上的实际值量化为 u 轴上的量化值。量化器函数 f 满足:
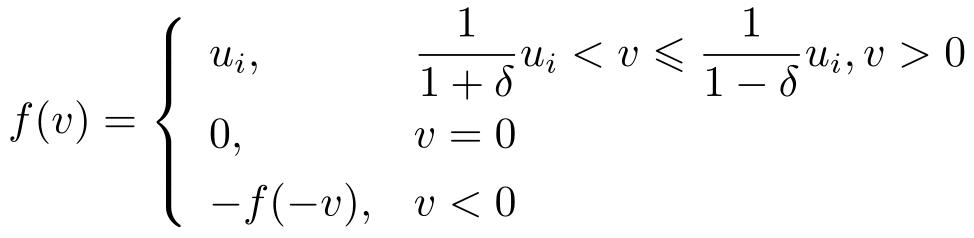
这里
 ,0<
δ
<1。采用对数量化器,量化误差
,0<
δ
<1。采用对数量化器,量化误差
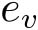 与实际值
v
的比值
δ
v
满足
与实际值
v
的比值
δ
v
满足
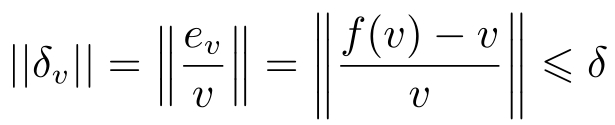
但这种量化器的量化区域越接近原点,量化分割越密集,因此所需码率不是有限固定的。这意味着对数量化器在实际应用中将受到限制。
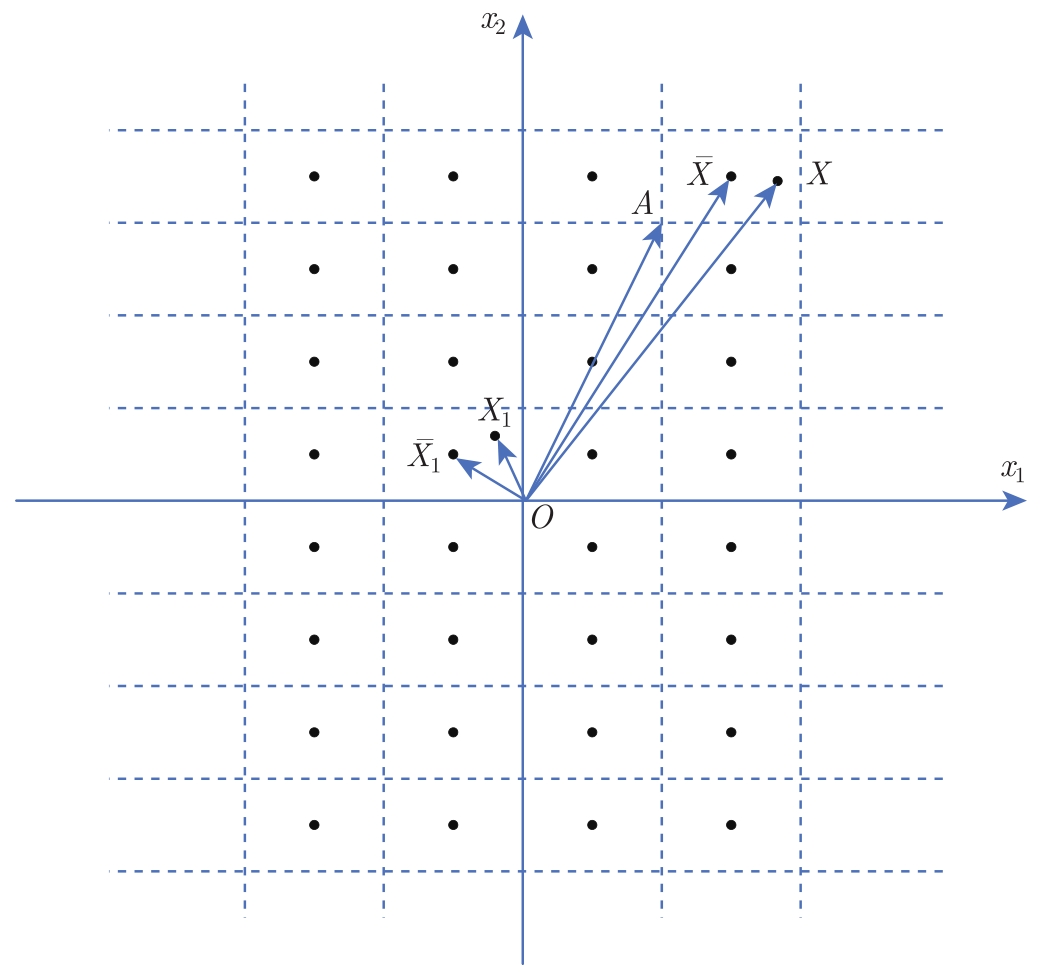
图2-1 二维均匀量化器
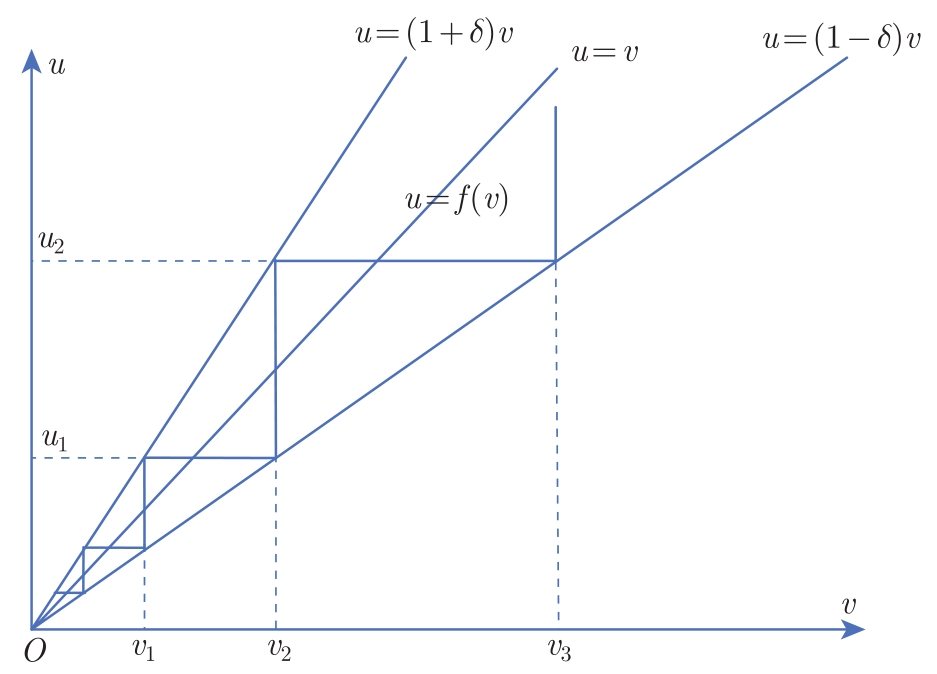
图2-2 对数量化器
针对均匀量化方法与对数量化方法的上述不足,本书提出并应用基于球极坐标系的量化器(简称球极坐标量化器)解决量化控制系统分析与设计问题。球极坐标量化器首先将直角坐标系表示的系统状态转换为球极坐标系表示的形式,然后在球极坐标系中进行量化。下面具体介绍球极坐标量化器,并给出这种量化器的一个重要性质。