




有限元法是最重要的工程分析技术之一,广泛应用于弹塑性力学、断裂力学、流体力学、热传导等领域。
大约在300年前,牛顿和莱布尼茨发明了积分法,证明了该运算具有整体对局部的可加性。虽然,积分运算与有限元法对定义域的划分是不同的,前者进行无限划分而后者进行有限划分,但积分运算为实现有限元法准备了理论基础。
在牛顿之后,著名数学家高斯提出了加权余值法及线性代数方程组的解法。这两项成果中前者被用来将微分方程改写为积分表达式,后者被用来求解有限元法得出的代数方程组。
在18世纪,另一位数学家拉格朗日提出了泛函分析。泛函分析是将偏微分方程改写为积分表达式的另一途径。
在19世纪末20世纪初,数学家瑞利和里兹(Rayleigh Ritz)首先提出了对全定义域运用展开函数来表达其上的未知函数。1915年,数学家伽辽金(Galerkin)提出了选择展开函数中形函数的伽辽金法,该方法被广泛地用于有限元分析。
20世纪40年代,随着航空业的飞速发展,人们需要对飞机结构进行精确的设计,在工程中逐渐产生了矩阵力学分析方法。1943年,数学家库朗德第一次提出了在定义域内分片地使用展开函数来表达其上的未知函数。这实际上就是有限元法的做法。
1955年,德国的Argyris出版了第一本关于结构分析中的能量原理和矩阵方法的书,为后续的有限元研究奠定了重要基础。1956年,波音公司的Turner、Clough、Martin和Topp在分析飞机结构时系统研究了离散杆、梁、三角形的单元刚度表达式。1960年,Clough在处理平面弹性问题时第一次提出并使用了“有限元”的名称。1967年,Zienkiewicz和Cheung出版了第一本有关有限元分析的专著。1970年以后,有限元法开始被用于处理非线性问题和大变形问题。
20世纪60年代初,我国老一辈计算科学家开始将计算机技术应用在土木、建筑和机械工程等领域。1964年,冯康教授独立于西方创造了一整套解微分方程问题的系统化、现代化的计算方法,即有限元法,并发表了论文《基于变分原理的差分格式》,这是中国学者独立于西方创立有限元法的标志。黄玉珊教授提出了“小展弦比机翼薄壁结构的直接设计法”和“力法-应力设计法”。1964年,崔俊芝院士研发了国内首个平面问题通用程序,并成功应用于解决刘家峡大坝复杂的应力分析问题。20世纪70年代,钱令希教授作了题为《结构力学中最优化设计理论与方法的现代发展》的报告。
有限元法也叫有限单元法(Finite Element Method,FEM),是随着电子计算机的发展迅速发展起来的一种弹性力学问题的数值求解方法。20世纪50年代初,它首先应用于连续体力学领域—飞机结构静、动态特性分析中,用于求得结构的变形、应力、固有频率及振型。有限元法具有有效性,应用范围已从线性问题扩展到非线性问题,分析对象已从弹性材料扩展到塑性材料、黏弹性材料、黏塑性材料和复合材料,从连续体扩展到非连续体。
图1-2所示为结构与有限元法。有限元法中的相邻的小区域通过边界上的节点连接起来,可以用一个简单的插值函数来描述每个小区域内的变形和应力。只计算节点处的应力或变形,非节点处的应力或变形是通过函数插值获得的。换句话说,有限元法并不计算区域内任意一点的变形或应力。
事实上,当划分的区域足够小时,每个区域内的变形和应力总是趋于简单,计算的结果逐渐接近真实情况。从理论上可以证明,当单元数目足够多时,有限元解将收敛于问题的精确解,但是计算量相应增大。因此,在实际工作中总是要在计算量和计算精度之间找一个平衡点。
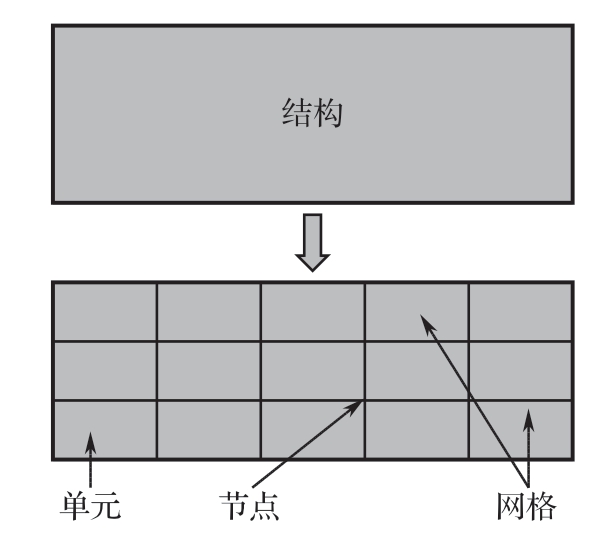
图1-2 结构与有限元法
有限元法在工程中的应用广泛且深入,特别是在结构优化领域,它已经成为一种不可或缺的工具。从结构形状的最优化到结构强度的分析,再到振动的分析,有限元法为工程师提供了强大的支持,帮助他们解决了一系列复杂的工程问题。
在过去的50多年里,有限元法已经发展成一个非常成熟的数值分析方法,为工程实践带来了巨大的经济效益。它的出现不仅使传统的基于经验的结构设计趋于理性,还推动产品设计向更加精细的方向发展。这主要体现在产品设计过程中样机试制次数的大幅减少,以及产品可靠性的显著提高。
在实际应用中,有限元法被广泛应用于各种工程领域。例如,在压力容器的设计中,有限元法可以应用于结构应力分析和形状优化,以确保压力容器的安全性和经济性。在机床切削过程中,有限元法可以应用于振动分析和减振设计,以提高机床的加工精度和稳定性。此外,在汽车研发过程中,有限元法可以应用于碰撞模拟,为汽车安全性设计提供重要的参考依据。在发动机设计过程中,有限元法可以应用于减振降噪分析,以优化发动机的结构设计,提高其性能和可靠性。同样,在武器设计过程中,有限元法可用于模拟爆轰和弹头形状优化,以确保武器的威力和精度。
计算机辅助工程(Computer Aided Enginnering,CAE)在现代工程设计中占据了至关重要的地位,其广泛的应用使得复杂的设计过程更加高效、精确和可靠。CAE的核心在于分析计算与仿真模拟,它涵盖了工程数值分析、结构与过程优化设计、强度与寿命评估,以及运动/动力学仿真等多个领域。这些领域的综合应用使得CAE能够全方位地验证未来工程或产品的实用性与稳定性,从而避免在实际生产过程中出现意外。
追溯CAE技术的起源,我们可以发现其主要归功于有限元法的诞生。在有限元法的发展初期,绝大多数CAE软件都是基于该方法进行计算求解的。随着计算机技术的飞速发展和有限元法的不断完善,CAE软件的功能和性能得到了极大提升。如今,CAE软件已经能够处理更加复杂的问题,如非线性分析、多物理场耦合分析、优化设计等,为工程师提供了更加强大和灵活的设计工具。
此外,随着云计算的发展,CAE软件实现了云端化,这使得工程师可以随时随地通过网络访问和使用CAE软件,大大提高了工作效率和便利性。人工智能的应用也给CAE软件带来了新的发展机遇,如智能优化设计、自动仿真等,这些技术的应用进一步推动了CAE软件的发展和创新。
总之,CAE软件作为现代工程设计的重要工具,其发展历程充分展示了科技进步对工程设计的巨大推动作用。随着技术的不断进步和创新,CAE软件将发挥更加重要的作用,为工程师提供更加高效、精确和可靠的解决方案。