




这是某君提出的问题。马先生对于我们提出这样的问题,好像非常诧异,他说:
“这不过是行程的问题,只需注意一个要点就行了。从前学校开运动会的时候,有一种运动叫作什么障碍物竞走,比现在的跨栏要费事得多,除了跨一两次栏,还有撑竿跳高、跳浜、钻圈、钻桶,等等。钻桶,属于全部通过的问题。桶的大小只能容一个人直着身子爬过,桶的长短却比一个人长一点儿。我且问你们,一个人,从他的头进桶口起,到全身爬出桶止,他爬过的距离是多少?”
“桶长加身长。”周学敏回答。
“好!”马先生说,“这就是‘全部通过’这类题的要点。”
例一: 长60丈的火车,每秒行驶66丈,经过长402丈的桥,自车头进桥,到车尾出桥,需要多长时间?
马先生将题写出后,便一边画图17-1,一边讲:
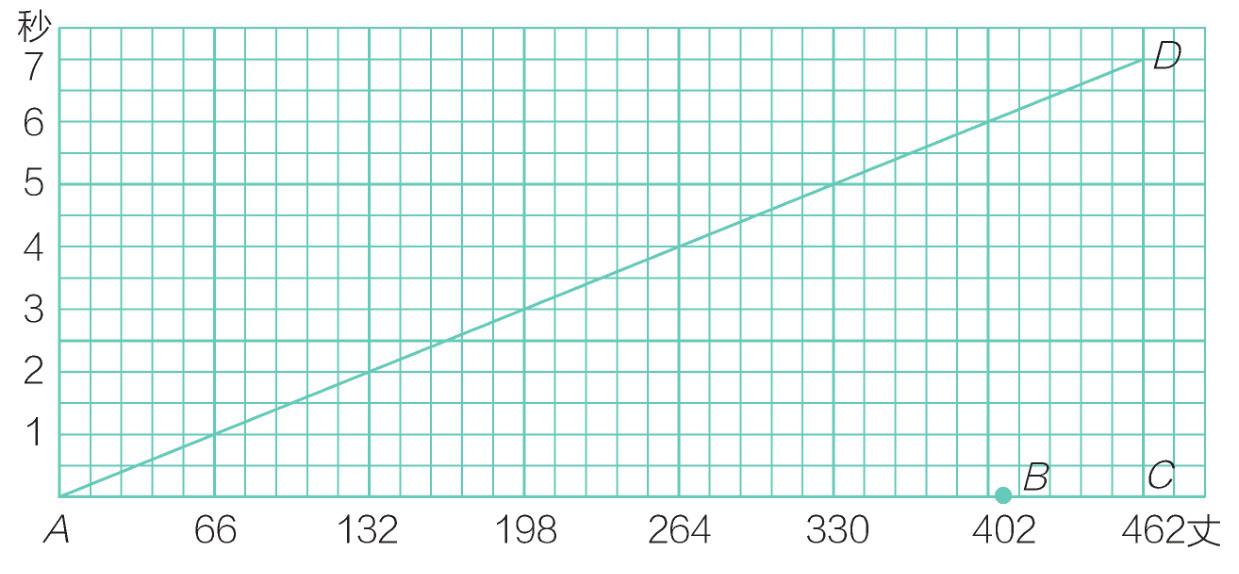
图17-1 例一图解
用横线表示距离,AB是桥长,BC是车长,AC就是全部通过需要走的路程。
用纵线表示时间。
依照1和66“定倍数”的关系画 AD ,从 D 横看过去,得7,就是要走7秒钟。
根据马先生的讲解,我且将算法补在这里:

例二: 长40尺的列车,全部通过长200尺的桥,耗时4秒,列车的速度是多少?
以前一个例题作蓝本,此题是知道距离和时间,求速度的问题。它的算法,我也明白了:

画图的方法,第一、二步与例一是相同的,不过第三步是连结 AD 得交点 E ,由 E 竖看下来,60便是列车每秒的速度,如图17-2所示。
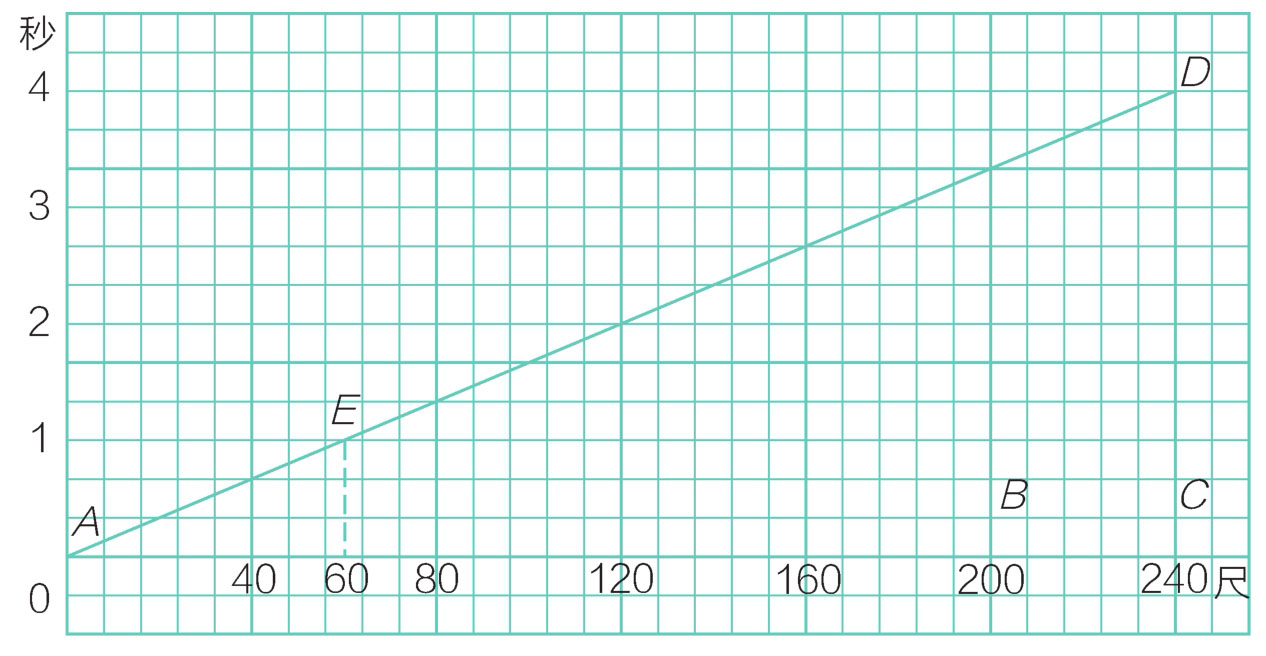
图17-2 例二图解
例三: 有人见一列车驶入240公尺长的山洞,车头入洞后8秒,车身全部入内,共经20秒钟,车完全出洞,求车的速度和车长。
这题最初我也想不透,但一经马先生提示,便恍然大悟了。
“列车全部入洞要8秒钟,不用说,从车头出洞到全部出洞也是要8秒钟了。”
明白这一个关键,画图真是易如反掌啊!如图17-3,先以 AB 表示洞长,20秒减去8秒,正是12秒,这就是车头从入洞到出洞所经过的时间,因得 D 点,连结 AD ,就是列车的行进线。——延长到20秒那点得 E 。由此可知,列车每秒钟行20公尺,车长 BC 是160公尺。
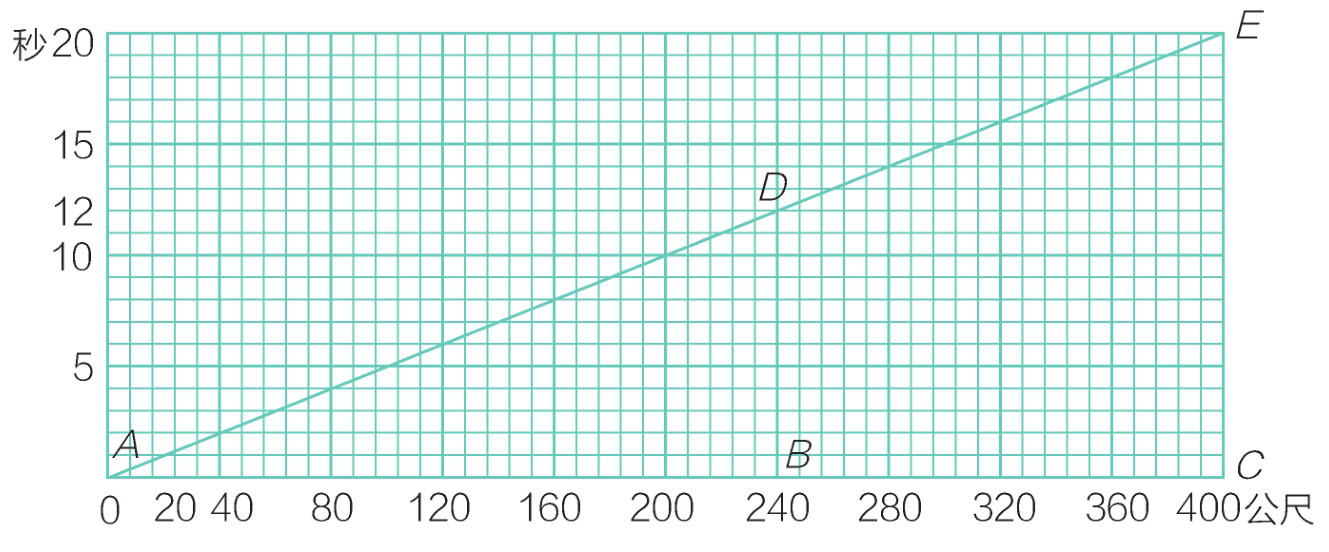
图17-3 例三图解
算法是这样的:
240公尺÷(20秒 - 8秒)= 20公尺/秒——列车的速度
20公尺/秒 × 8秒 = 160公尺——列车的长
例四: A、B两列车,A长92尺,B长84尺,相向而行,从相遇到相离,经过2秒钟。若B车追A车,从追上到超过,经8秒钟,求各车的速度。
马先生指定周学敏解答这道题,于是他边画图(如图17-4所示)边说:
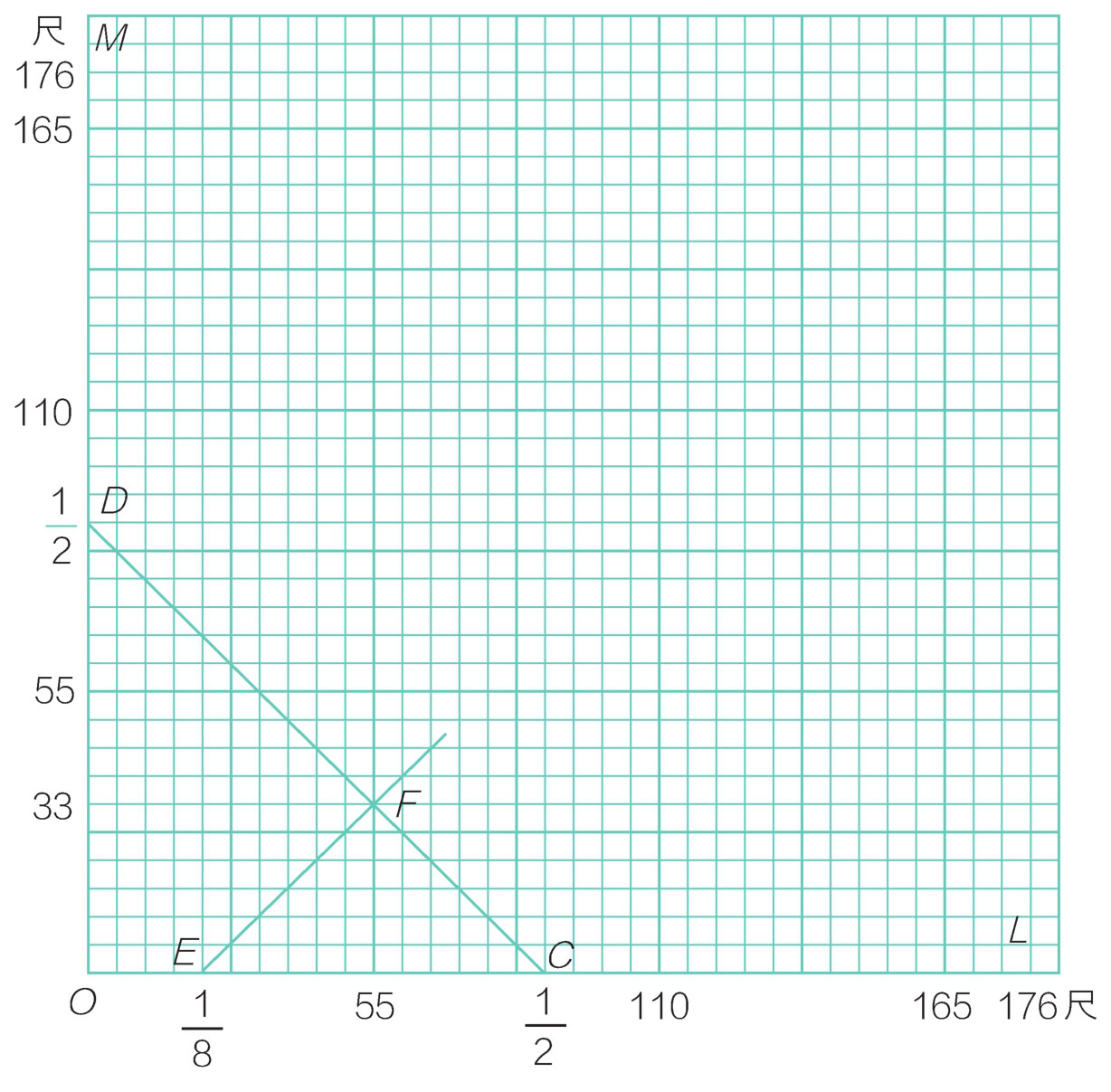
图17-4 例四图解
“第一,依‘全部通过’的要点,两车所行的距离总是两车长的和,因而得 OL 和 OM 。
“第二,两车相向而行,每秒钟经过的总距离是它们速度的和。因两车2秒钟相离,所以这速度的和等于两车长的和的1/2,因而得 CD ,这是表‘和一定’的线。
“第三,两车同向相追,每秒钟所追上的距离是它们速度的差。因8秒钟追过,所以这速度的差等于两车长的和的1/8,因而得 EF ,这是表‘差一定’的线。
“从 F 竖看得55尺,是B的速度;横看得33尺,是A的速度。”
经过这样的说明,算法自然容易明白了:
