




悬浮架位于车体的下部,通过电磁铁从外侧环抱轨道。其基本结构组成为5个基本悬浮架单元+横向机械控制系统(图2-20)。5个基本悬浮架单元从结构以及载荷传递上相对独立,各自实现与轨之间匹配。横向机械控制系统主要包含两组迫导向机构以及滑台装置,通过横向机械控制系统锁定5个悬浮架单元理想状态的横向位置,既实现了车辆内部之间的运动关系,又均匀传递了车体与悬浮架之间横向载荷。另外,悬浮架还包括第三轨受流器、扫石器等附属装置。因此,针对悬浮架结构运动及动力学特征,可以通过独立悬浮架单元以及横向机械控制系统两个方面来描述。
磁浮车辆车体由5组悬浮架单元共同支撑,其结构包括模块装配、电机悬挂装置、牵引装置、支撑轮装置、垂向滑橇装置、空气弹簧装置、空气管路、液压管路(图2-21)。根据不同的悬浮架单元位置,选择性布置基础制动装置、测速定位装置。
在受车体结构约束的情况下,对于悬浮架单元而言,每个单元都必须适应各种线路要求,在直线、过渡曲线、圆曲线的运动过程中,左右模块之间需要满足三个方向的自由度:前后错位适应内外轨不同弧长变化;左右拉开适应轨距要求;模块点头运动适应线路扭转。这部分功能主要通过悬浮模块实现。模块结构如图2-22所示。
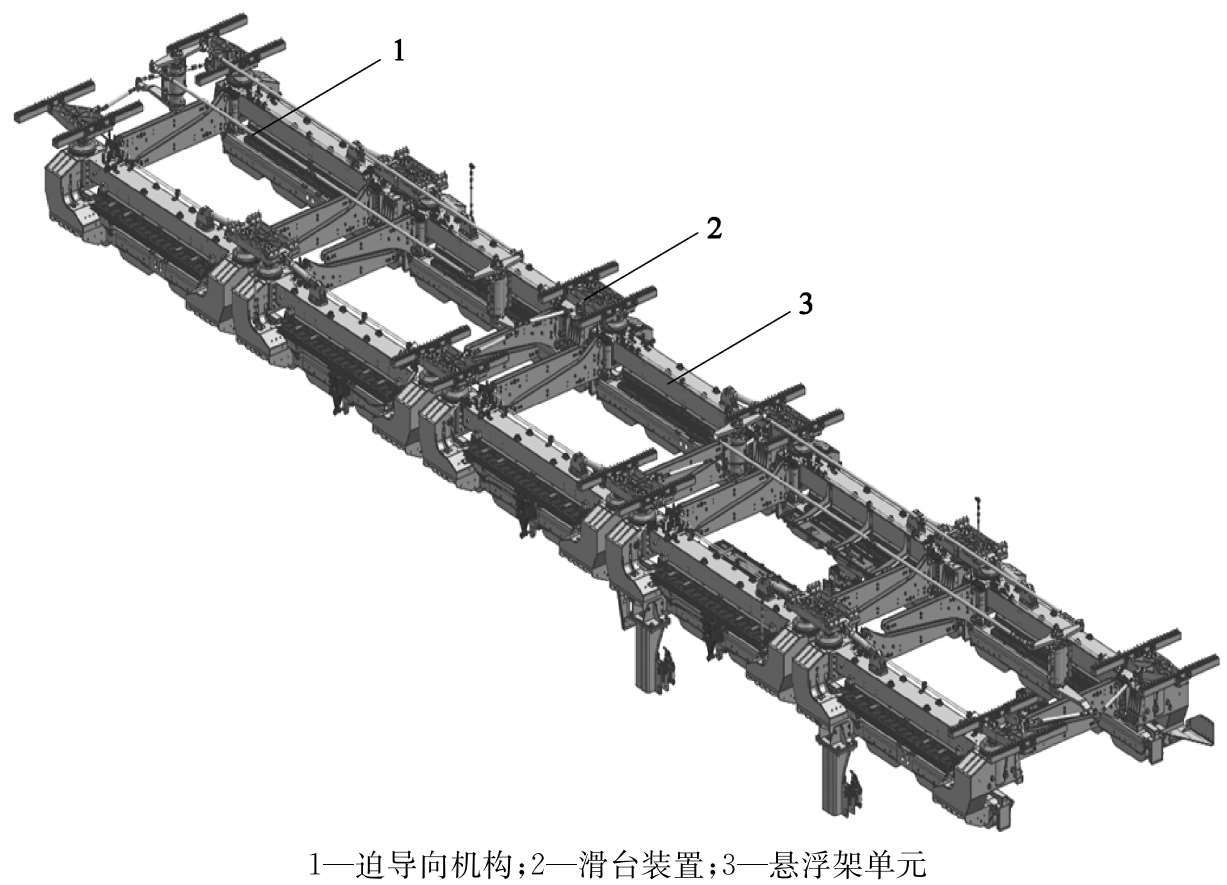
图2-20 悬浮架总图
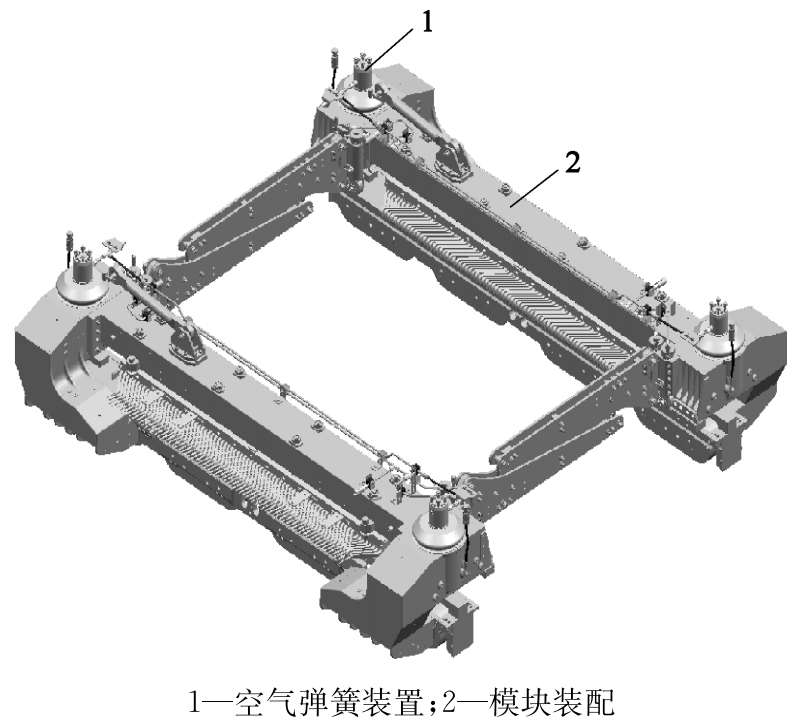
图2-21 悬浮架单元
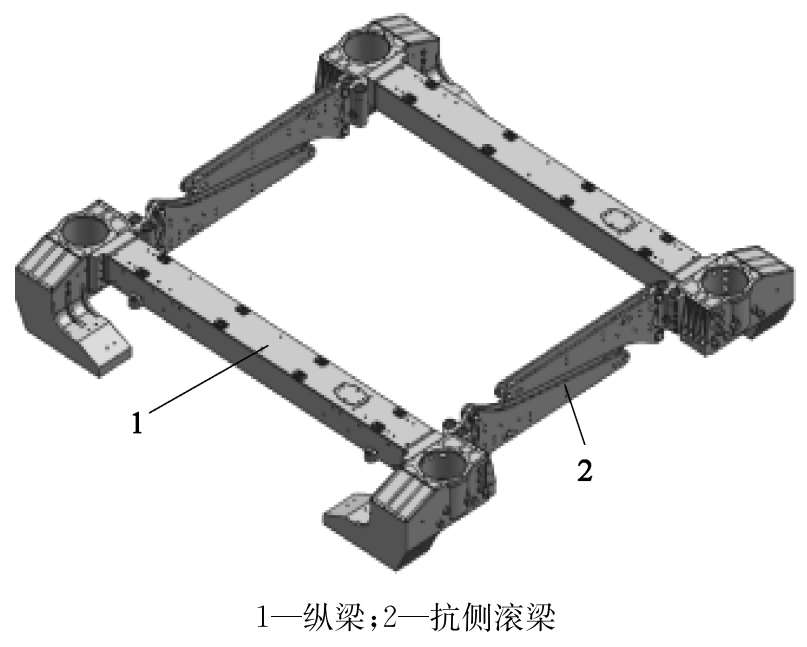
图2-22 模块结构
根据《磁浮铁路技术标准(试行)》(TB 10630—2019)规定,线路的最大横坡扭转率不宜大于0.12°/m(注:《长沙磁浮交通工程设计暂行规定2015》规定线路的最大横坡扭转率不宜大于0.1°/m),而最大横坡角为6°。基于一般情况,最大横坡角为6°,扭转率设置为0.1°/m,所以缓和曲线的长度至少要60m以上。分析侧滚梁工作时考虑最坏的工况,故取较短缓和曲线的长度 S =60m。
在缓和曲线上,曲线半径由直线部分的无穷大均匀变化为圆曲线的半径,其半径随缓和曲线的位置按选定的函数关系(比如三次抛物线)变化,超高也由零变为圆曲线的常数。由于存在超高的变化,故磁浮列车通过缓和曲线时,模块要发生扭曲。
由前面计算已知缓和曲线长度 S =60m,则超高侧悬浮架的扭转角 Φ 可由下式算得:
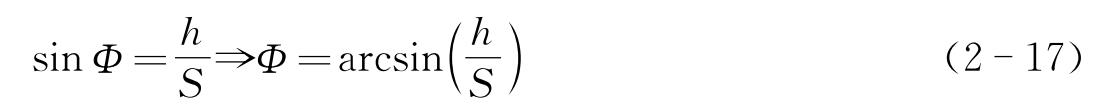
技术要求规定线路的最大横向坡度为6°,轨距为1.86m,则线路最大超高
h
=1860×sin 6°≈194mm,代入式(2-17)可解得扭转角
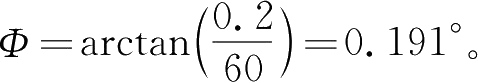
以最坏的情况来考虑模块扭转所产生的垂向位移。这里假设列车过曲线时,悬浮模块以模块端部为扭转中心,如式(2-18)所示,则前后两抗侧滚梁垂向位移分别为


式中 L M1 ——扭转中心到后抗侧滚梁的距离;
L M2 ——扭转中心到前抗侧滚梁的距离。
取 L M1 =253mm, L M2 =2 507mm,代入式(2-18)、式(2-19),可解得Δ Z 1 =0.84mm,Δ Z 2 =8.36mm。
故可得,若要不约束悬浮架过缓和曲线时模块所产生的扭转,就要求抗侧滚梁结构在垂向上能提供约9mm的运动余量。
抗侧滚梁通过安装支座与模块连接,故悬浮列车过曲线,左右模块发生错位时,抗侧滚梁安装支座同样也发生错位,并且错位量与模块相同。
左右模块通过曲线时的几何形态如图2-23所示。由于直线导轨副的作用,左右滑台和车体纵向位置不能改变,而且始终要和车体中心线保持垂直,图2-23中标出了6位滑台的连线。滑台和模块靠纵向拉杆连接,所以模块和滑台纵向移动量很小。因此,图中L1/R1、L2/R2、L4/R4和L5/R5都要发生错位,从原先的矩形结构错位成平行四边形结构,计算得出:


式中 D ——左右模块距离(取轨距1.86m);
β ——列车过R 75m曲线时模块偏转角。
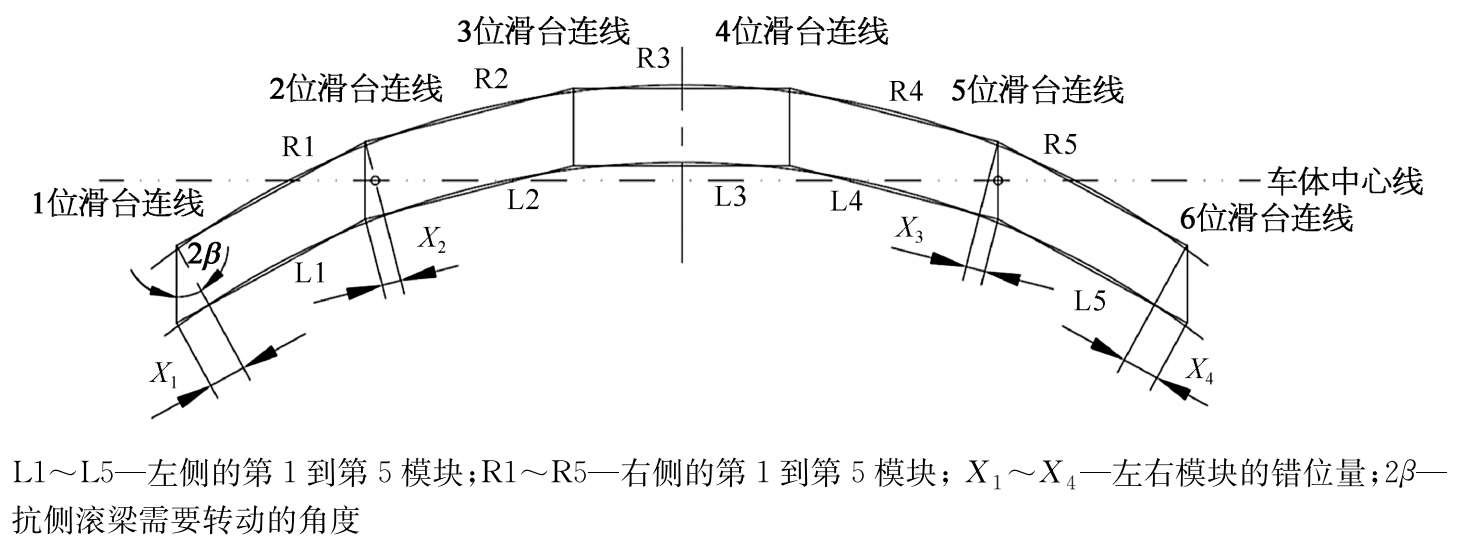
图2-23 整车过曲线几何形态
过R 75m曲线时,计算得出 X 1 = X 4 ≈141.4mm, X 2 = X 3 ≈70.7mm。
从计算结果可以看出,过R 75m曲线时,左右模块的错位量很大。牵引杆和滑台、模块的销连接如果有间隙的话也提供不了141.4mm的错位量。抗侧滚梁由两块铝板连接而成,两块铝板之间的距离也不可能提供这么大的错位量。所以只能通过抗侧滚梁绕根部安装轴转动来提供错位量。
与此同时,如果考虑曲线上轨距不变,抗侧滚梁偏转后,左右片梁将被拉开,端部拉开的尺寸距离大约为12mm。
横向机械控制系统主要包含两组迫导向机构以及滑台装置。整车左右两侧各有6个滑台,按其功能分为固定滑台和移动滑台。通过固定滑台设置确定车体与悬浮架的相对位置,形成车体通过曲线时的两个理论固定转心。移动滑台设置直线轴承,车体与滑台之间能够自由横向移动。
悬浮架和车体的连接形式影响着整列磁浮车辆在曲线上的运动学形态。磁浮车辆悬浮架在三个方面和车体发生连接,如图2-24所示。
(1)直线导轨副。直线导轨副的滑块安装在滑动台上,滑轨与车体底部采用螺栓连接,整个悬浮架与车体有16副直线导轨副配合。这样车体通过直线导轨副配合相对于构架可以发生横移,列车通过曲线特别是半径很小的曲线时,就会产生较大的相对横移,由于牵引杆连接滑台与模块,纵向牵引、制动力将由滑台直接传递到车厢。
(2)迫导向机构转动销与车体的销接。整车装两套迫导向机构,与车体共有四处销接。在曲线上某些左右滑块的中心点在被动导向力的作用下将占据接近线路中心线的位置(图2-25中的 D 点),该图中 A 点则相当于车体与下部悬浮架的固定转动点,由于连杆的定位, A 点将基本保持在线路中心线上,而车体销接点 B 、 C 将偏离左右模块中心线,通过机构作用强迫悬浮架导向。
(3)滑台和车体的连接。第2和第5位滑台与车体刚性连接,连接处( A 点)构成了整车过曲线时的转动中心。
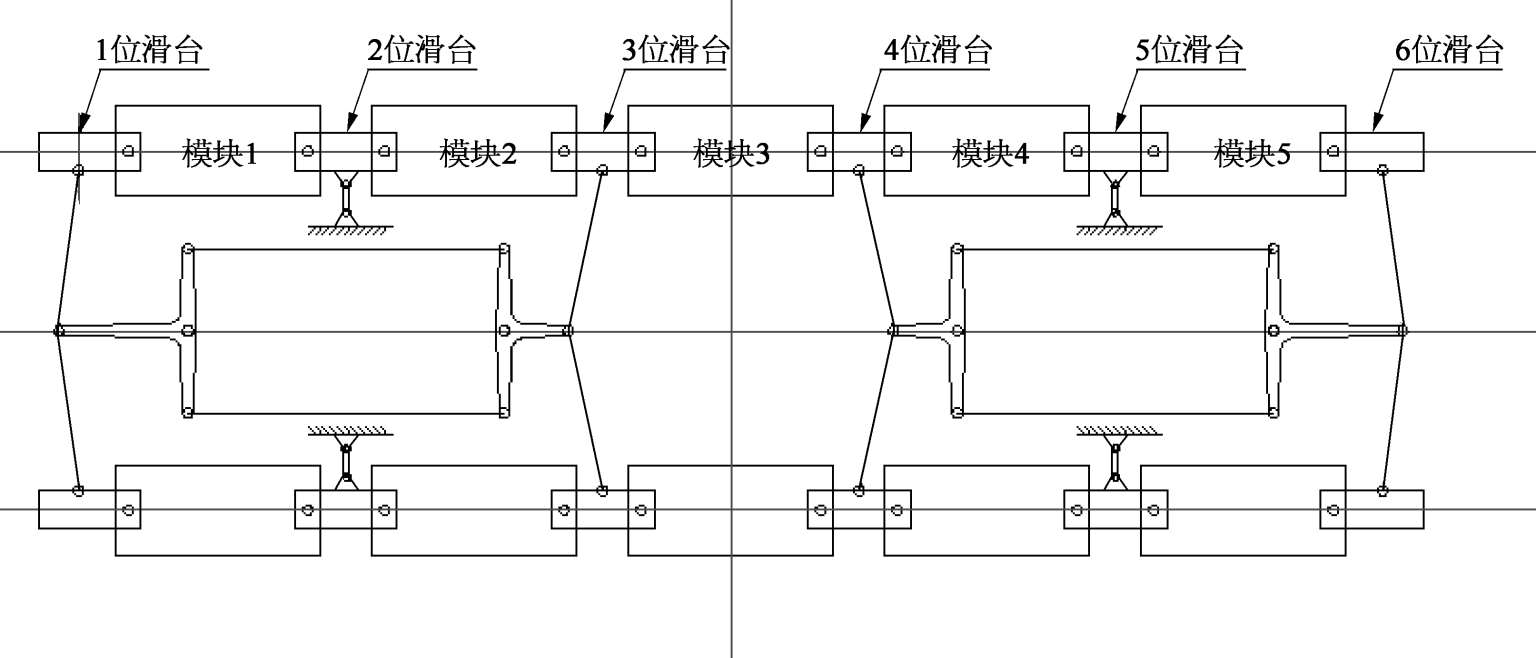
图2-24 悬浮架和车体的连接
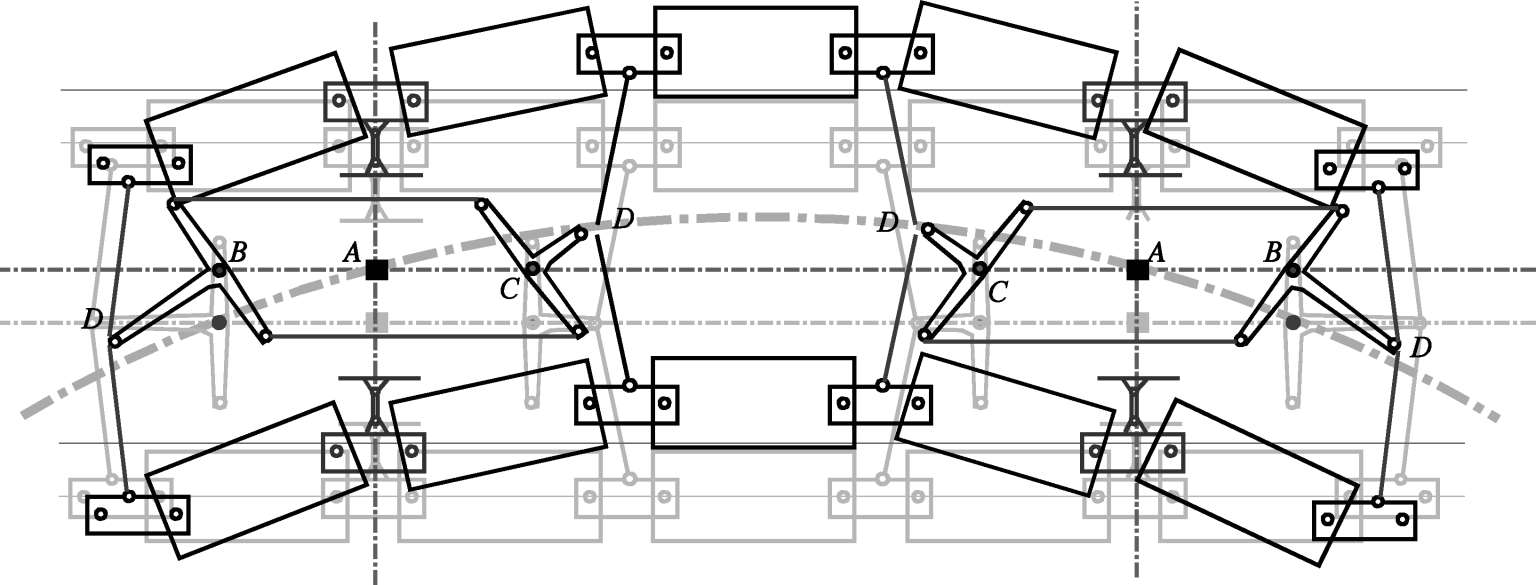
图2-25 通过曲线时车体与悬浮架的位置与迫导向原理
悬浮架和车体的连接方式构成了车辆过曲线的几何约束:
(1)当车辆通过曲线时,车辆的模块(5对/车)由于导向力作用,将紧随线路排列成曲线形状。此时,由于车体为一刚体,不能随曲线弯曲,各模块相对车体将产生平移和转角,由直线导轨副保证车体和模块之间的平移量。
(2)各个直线导轨副以及转臂和车体的销接点由于车体的刚性,纵向(弧长方向)距离不会变化。
(3)第2和第5位滑台横向于车体刚性连接,即在曲线上,第2和第5位左右滑台连线的中点始终是在车体中心线上的,这两个中点其实构成了5个悬浮模块过曲线的转动中心。这是曲线通过运动学分析的基础。不管悬浮模块相对于曲线是怎样的形态(内接、外切、相交),车体中心线始终是第2和第5位左右滑台中点的连线。
悬浮架模块在曲线上的状态是磁浮车辆曲线通过分析的基础,是磁浮车辆曲线通过状态和各相关结构的几何关系分析的依据。
模块在曲线受到导向磁力、离心力、二系悬挂力和重力横向分力等共同作用,模块的状态是这些力综合作用的结果。模块在曲线的状态下可以分为相切、内接、相交以及内外横向滑橇和曲线接触极限状态等不同的情况。受力分析如图2-26所示。
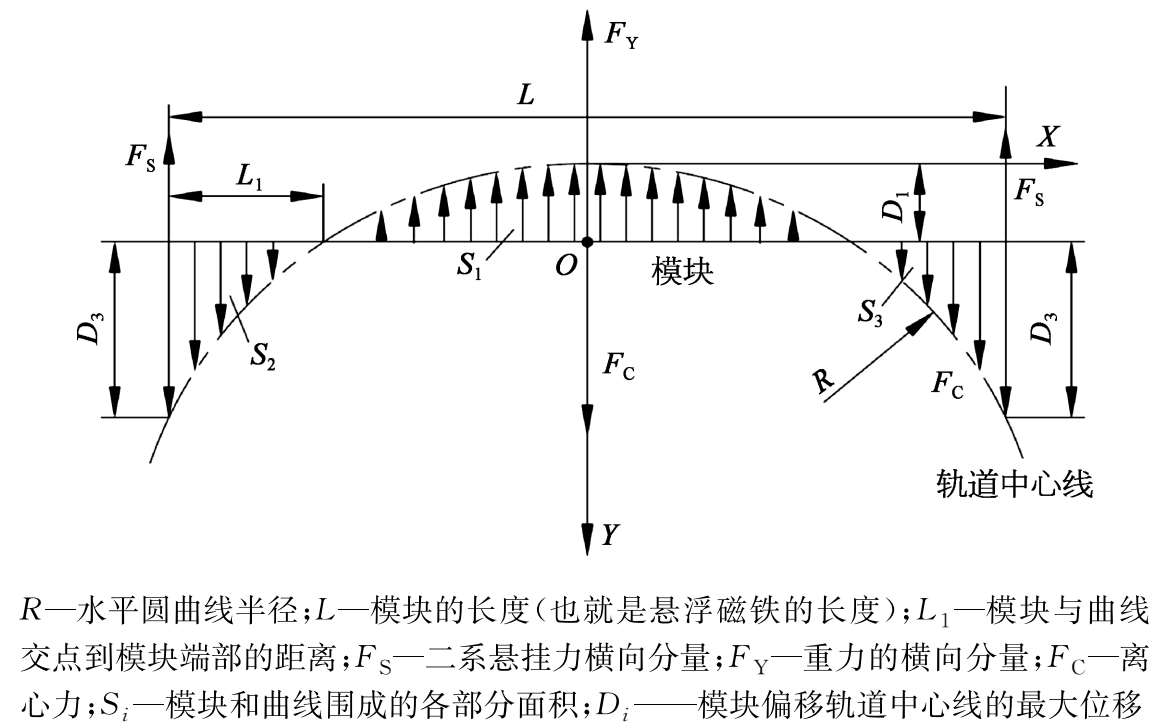
图2-26 模块在曲线上的受力图
模块沿曲线分布着导向磁力,导向磁力的大小与导向磁铁相对于轨道中心线的偏移量成正比,方向如图2-26所示。导向磁力的计算如下:

式中 F 0 ——一个电磁铁的轴线与轨道轴线对齐时的额定悬浮力;
z ——悬浮气隙;
W m ——磁极宽度;
d ——电磁铁的轴线与轨道轴线的偏移量。
几何曲线通过分析时,可以只考虑导向磁力的影响。只要模块内外导向磁力相等,模块就能够平衡地通过曲线。从图2-26可以看出,为了使模块受力平衡,要求对式(2-22)在面积 S 1 上的积分等于在面积 S 2 和 S 3 上的积分之和:
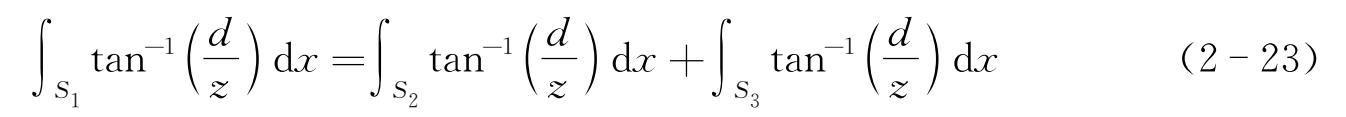
通过计算得到,随着曲线半径的增大, D 2 = D 3 =2 D 1 时,导向力平衡;在小曲线半径时, D 2 = D 3 ≈2 D 1 时,导向力达到平衡。所以几何曲线通过分析时,取平衡位置为 D 2 = D 3 =2 D 1 处。
以上分析考虑的只是模块的几何曲线通过,实际中模块还要受到悬挂力、离心力和重力横向分量。当模块正好以一定的速度平衡通过曲线时,模块正好在这样的位置达到受力平衡。如果模块通过曲线的速度增大(或减小)或者受悬挂力的影响,模块就向外轨(或向内轨)横移,相对调整导向磁力的增大(或减小),从而达到受力平衡。可以说,曲线通过时平衡位置一直在 D 2 = D 3 =2 D 1 处左右。
在模块受到很大的横向力的情况下(如较大的侧风、大的曲线通过速度),横向力超过轨道所能够提供的最大导向磁力,模块向外轨移动,直到轨道和模块上的横向滑橇接触,靠横向滑橇提供横向力来导向。
在对车体几何曲线通过分析时,常常假设模块和曲线是内接的。因为内接时相关结构几何状态往往是极限情况,按这种假设计算出的各种几何量是极限值,为曲线通过提供判断依据。模块和曲线相交或外接时,相当于过比曲线半径更大的曲线,曲线通过性更好。所以几何通过时经常采用模块和曲线内接的方式进行简化分析,求出的就是最极限的值。
在车辆过曲线时,车体在滑台的滑槽上横向滑动,不同位置的横向位移不相等。车辆通过越小的曲线,车体相对于悬浮模块的横向位移就越大。而且当单个悬浮模块和曲线内接时,车体的横向位移也最大。模块相对于曲线如果是其他形态,车体相对横移量会略小一些。所以几何曲线通过分析时,假设单个悬浮模块和曲线内接。模块水平圆曲线通过分析如图2-27所示。
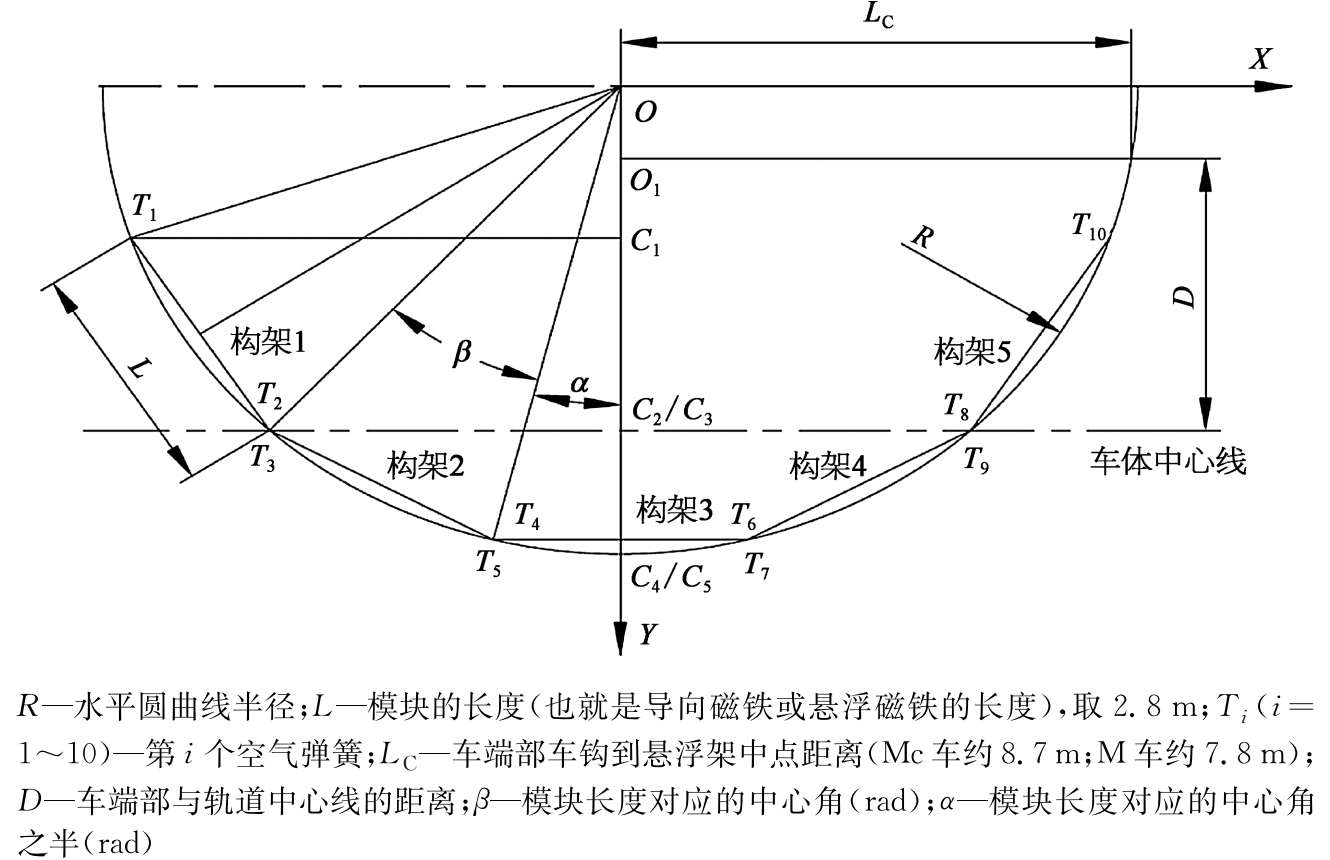
图2-27 模块水平圆曲线通过分析
车辆的侧滚刚度很大,可以认为车厢的侧滚角等于各模块单元的侧滚角,也就是说车厢底板与构架平面仍然保持平行。
模块通过水平圆曲线的几何分析如下:水平面内建立直角坐标系(图2-27),沿轨道的前进方向建立 X 轴,以圆曲线的中心建立坐标原点 O , Y 轴通过原点 O 且垂直于 X 轴,其方向指向曲线外侧。
车厢地板下面与模块销接,每车四个销接点,每半车两个。在迫导向机构的作用下,车体中心线位于图2-27所示位置。
考虑结构的对称性,只讨论半车模型。因为 L 远小于 R ,有
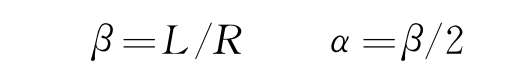
在△ OT 2 C 2 中,
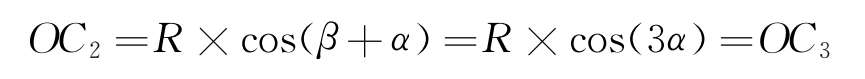
同理可得:
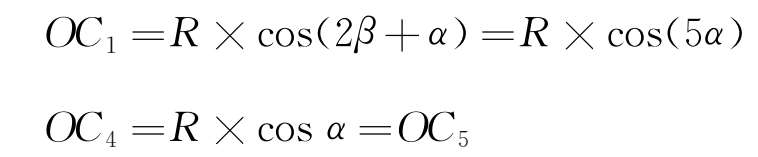
曲线半径取R 75m时,车体横向偏移量为
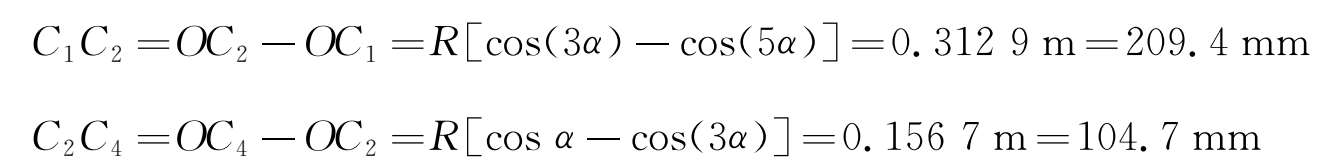
根据结构要求,模块1~5各安装上空气弹簧,同侧相邻两个空气弹簧及端部第1、第10两个空气弹簧上安装滑块平台,滑块平台与车体底架下平面之间横向可相互滑动,纵向不能相互移动。第1个空气弹簧上的滑块平台的滑动量为210mm。第2、第3个空气弹簧上的滑块平台的滑动量很小(如果刚性连接在车体上,滑块平台成为车厢的转动中心,横向几乎不会滑动)。第4、第5个空气弹簧上的滑块平台的滑动量为105mm。
因此,滑台上总滑动量设计值应至少达到±210mm。
由图2-27可知,车端部与轨道中心线的距离 D 为
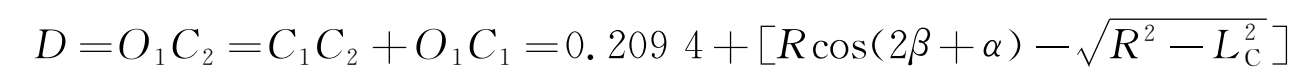
计算可得:

(1)迫导向机构的设计。从前面的分析可知,模块1滑台与车体的横向距离为312.9mm,模块3滑台与车体的横向距离为156.7mm。
迫导向机构过曲线时的运动学形态如图2-28所示,由于对称性,图中只画出了前三个模块。
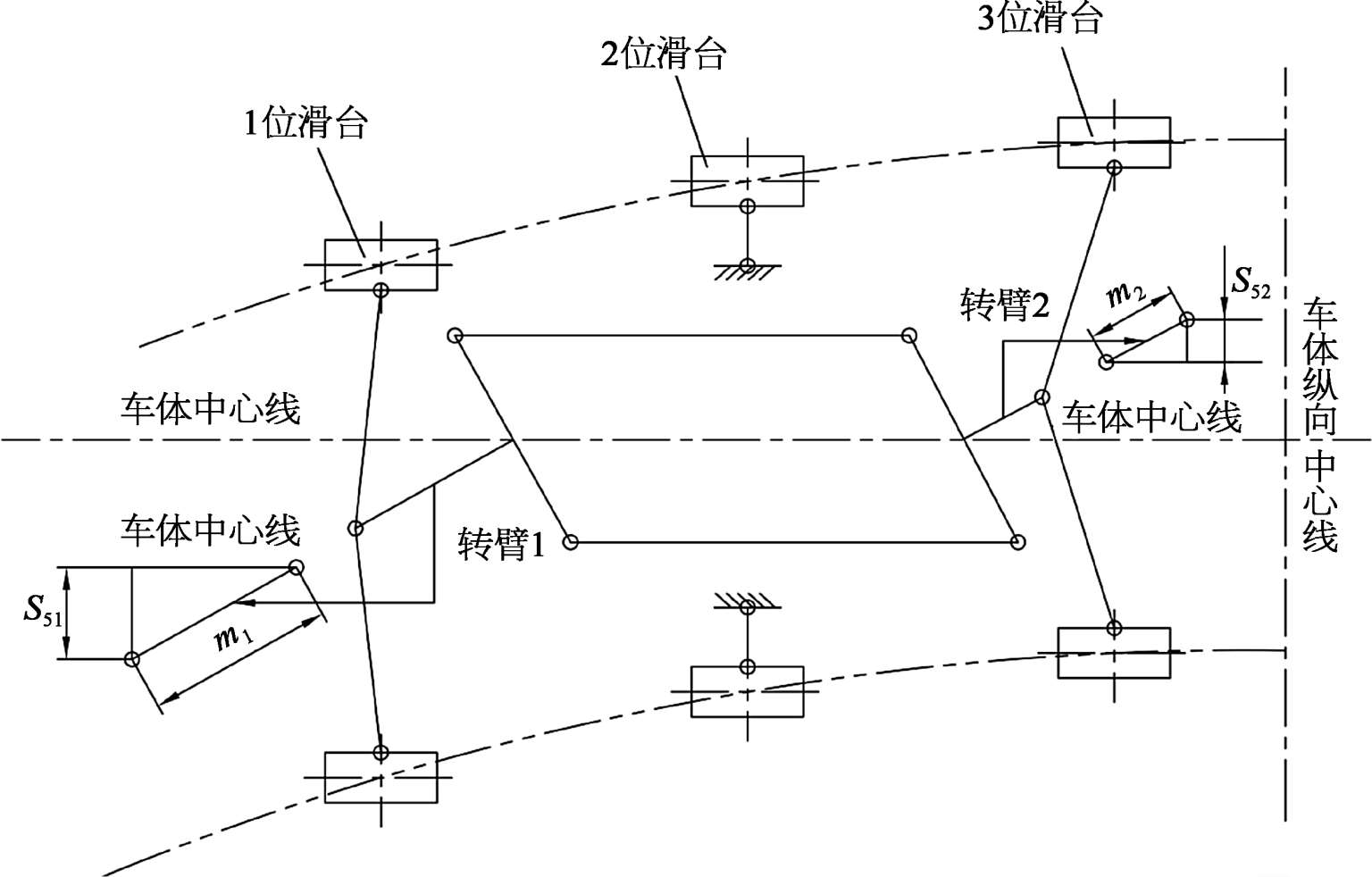
图2-28 钢缆平行四边形过曲线的运动学形态
图2-28中, S 51 为模块1滑台与车体的横向距离, S 51 =312.9mm; S 52 为模块2、3共用滑台与车体的横向距离, S 52 =156.7mm; γ 为转臂转过的角度; m 1 、 m 2 为转臂长。
γ 取值大,转臂就可以设置短一些; γ 取值小,转臂就必须设置长一些。 γ 受结构限制,不宜太大。设计时选定 γ =35°。
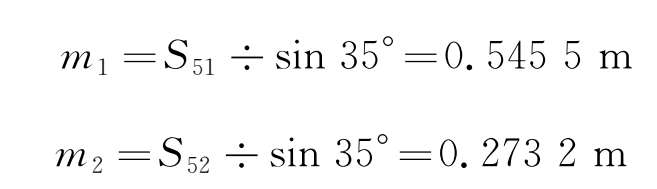
故取 m 1 =0.6m, m 2 =0.3m。
在R 50m曲线上,转臂实际的转角
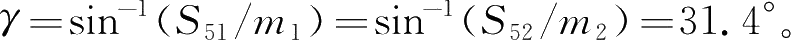 过曲线时,一般情况下模块和曲线是相交的,即
S
51
要小于312.9mm,实际的转角也略小于31.4°。
过曲线时,一般情况下模块和曲线是相交的,即
S
51
要小于312.9mm,实际的转角也略小于31.4°。
(2)曲线通过和迫导向机构的关系。迫导向机械机构和空气弹簧构成了悬浮架的悬挂系统,由空气弹簧垂向刚度传递垂向载荷,迫导向机构和空簧的横向刚度传递横向载荷。当车体在曲线上受到未平衡离心力和侧风影响时,钢管平行四边形机构的形态和受力情况如图2-29所示。
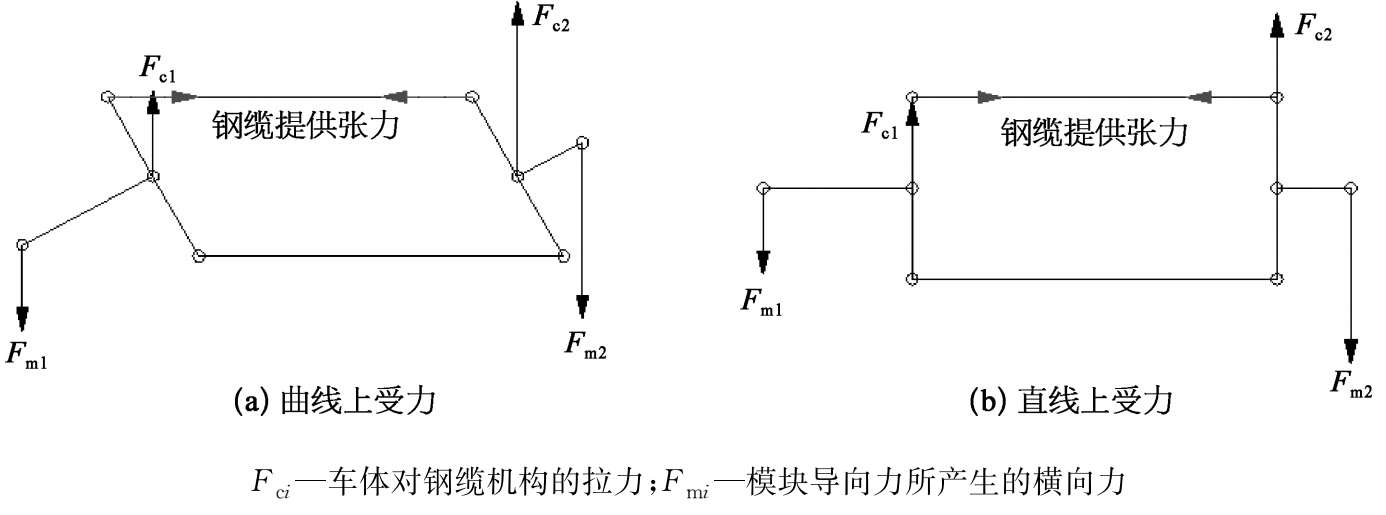
图2-29 钢管平行四边形机构受力分析
从受力分析图中可以看出,整个迫导向机构力是平衡的,而且
F
m
使转臂对中心销有一定的转矩:
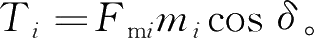 其中,
m
i
为各转臂的长度;
δ
为转臂转过的角度。
其中,
m
i
为各转臂的长度;
δ
为转臂转过的角度。
由于钢缆的作用, T 1 = T 2 ,从而可以推导出:
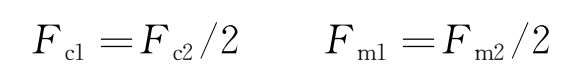
也就是整个迫导向机构可以把横向力(未平衡的离心力和侧风力)平均地分配到各个模块的悬挂系统上,使所有的模块受力状态相同,从而使得各个模块沿着曲线达到最合理分布。
基于悬浮架单元垂向动力学特征,通常考虑沉浮、侧滚和点头三个运动,而忽略横移运动和摇头运动。悬浮架单元结构如图2-30所示,在轨道上的动力学模型如图2-31所示。悬浮架单元主结构为左右以及前后对称结构,基于此,通过右半部分以及前半部分的受力分析就可以获知整个悬浮架的受力情况。悬浮架左、右模块为刚体,模块之间通过前、后两组弹簧阻尼单元连接,可用 K b 、 C b 表示,这里刚度和阻尼可能来源于弹性件以及结构件两个方面。每个刚体都有三个自由度,分别为沉浮、侧滚和点头。 F 1l 、 F 2l 、 F 1r 和 F 2r 分别为车体通过四个空气弹簧传给悬浮架的作用力。
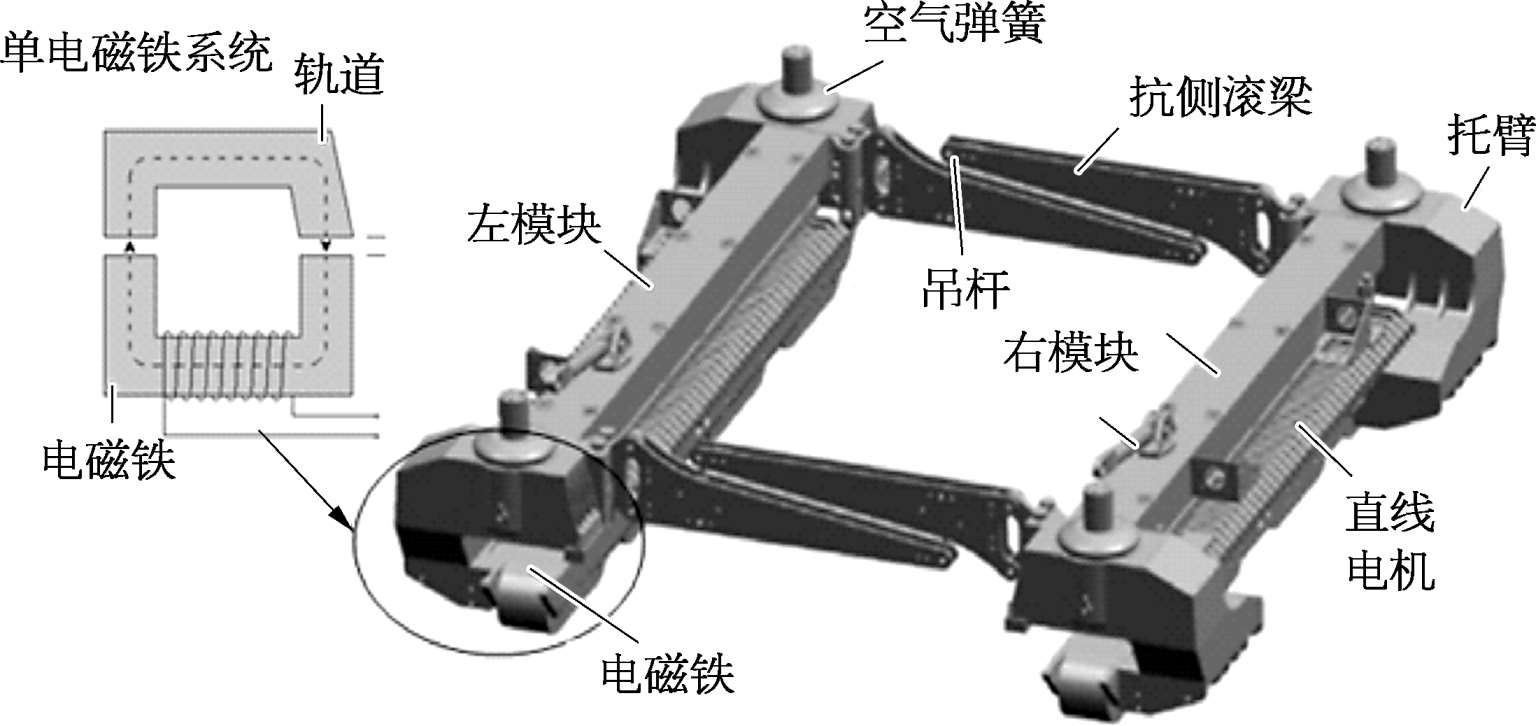
图2-30 低速磁浮列车悬浮架单元结构
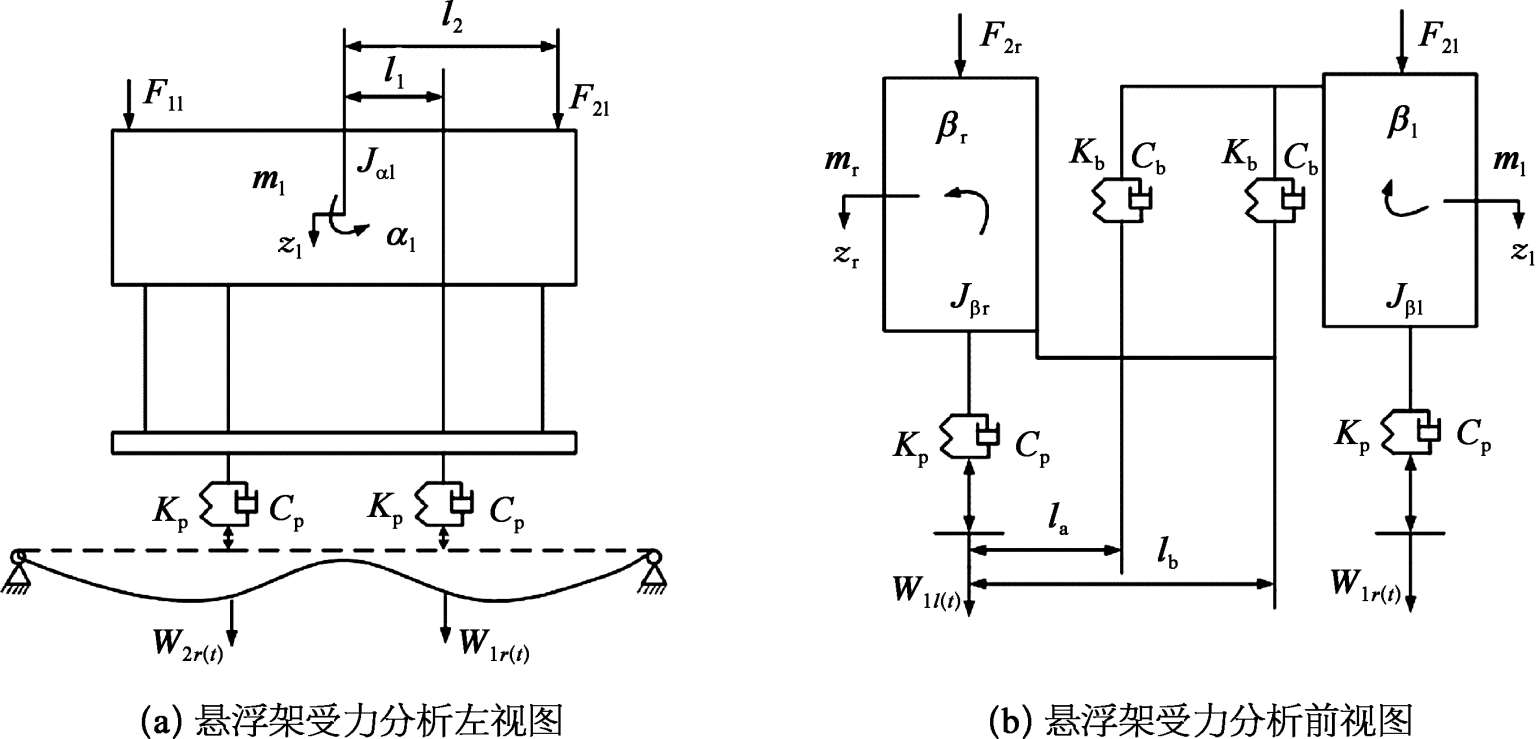
图2-31 悬浮架动力学模型
电磁力 F zij 和吊杆力 F bij 可由下式描述:
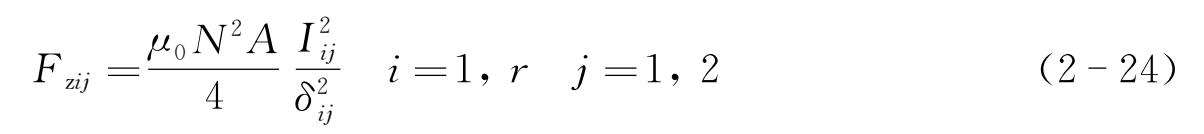
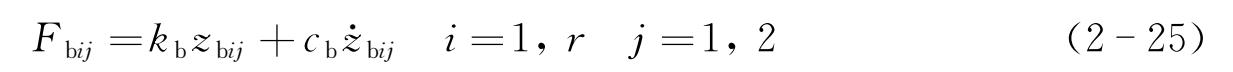
式中 I ij ——电磁铁电流;
μ 0 ——空气磁导率;
N , A ——电磁铁线圈匝数和磁极面;
δ ij , z b ij ——悬浮气隙和吊杆的形变,可由悬浮架的左、右模块位姿的参数和几何约束解出。
在研究车轨动力学问题时,将电磁铁与轨道梁之间的电磁力在系统平衡点处进行线性化,进而等效为弹簧阻尼力(磁隙刚度 K p 和磁隙阻尼 C p ),采用达朗贝尔原理和虚功原理,可以得到考虑沉浮、侧滚和点头三个自由度的整个悬浮架动力学方程。
沉浮运动:
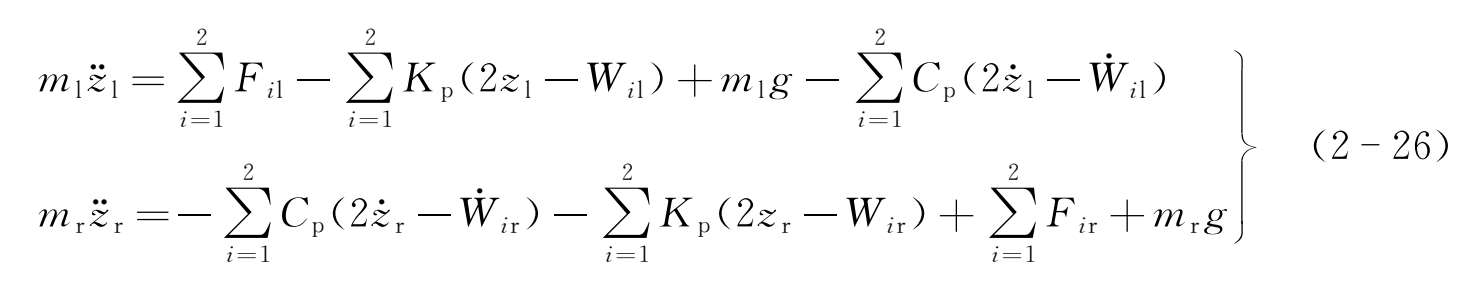
侧滚运动:
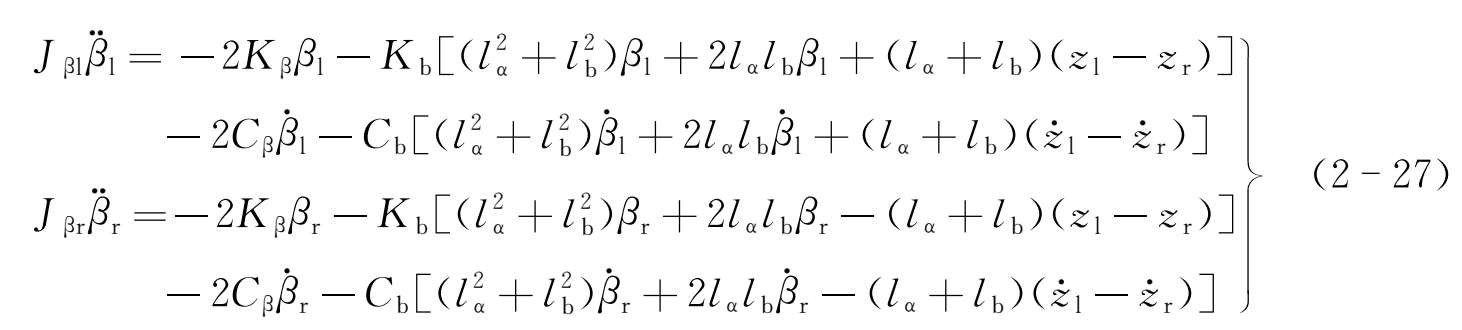
点头运动:
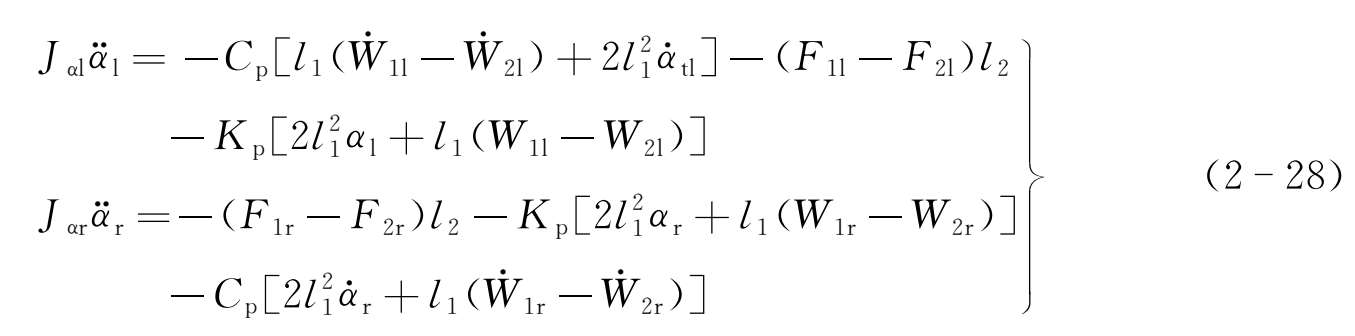
式中 K p , C p , K β , C β ——电磁力垂向刚度和阻尼,以及侧滚角刚度和阻尼;
K b , C b ——等效抗侧滚装置的刚度和阻尼;
F 1l , F 1r , F 2l , F 2r ——左前、右前、左后和右后的空气弹簧作用在悬浮架上的车体垂向载荷;
W 1l , W 1r , W 2l , W 2r ——左前、右前、左后和右后的轨道不平顺性;
z 1 , z r , α l , α r , β l , β r ——悬浮架单元的左右两边的垂向位移、点头角度和侧滚角度。
选取
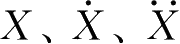 分别为广义的位移、速度和加速度,定义如下:
分别为广义的位移、速度和加速度,定义如下:
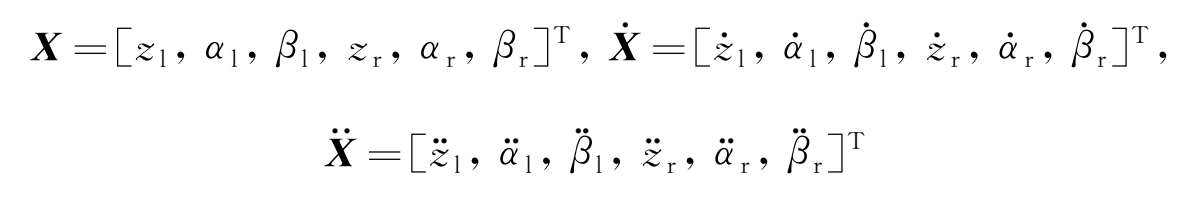
选取 M 、 C 、 K 和 P 分别表示质量矩阵、阻尼矩阵、刚度矩阵和广义载荷矩阵,由式(2-26)~式(2-28)可知其具有如下形式:
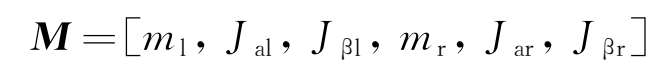
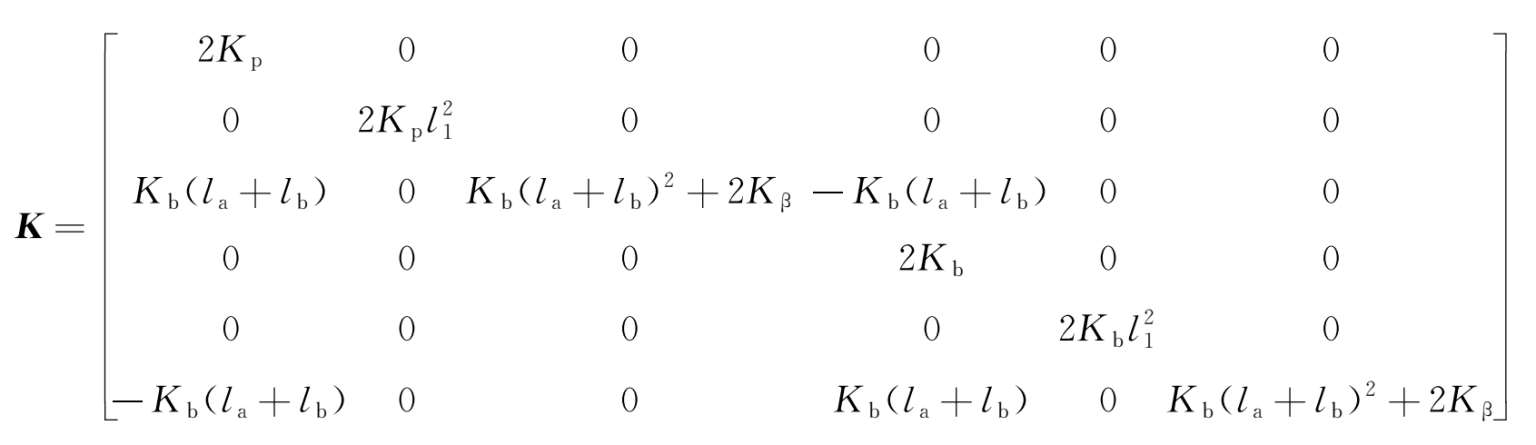

因此,悬浮架单元动力学方程[式(2-26)~式(2-28)]可由下式统一描述:

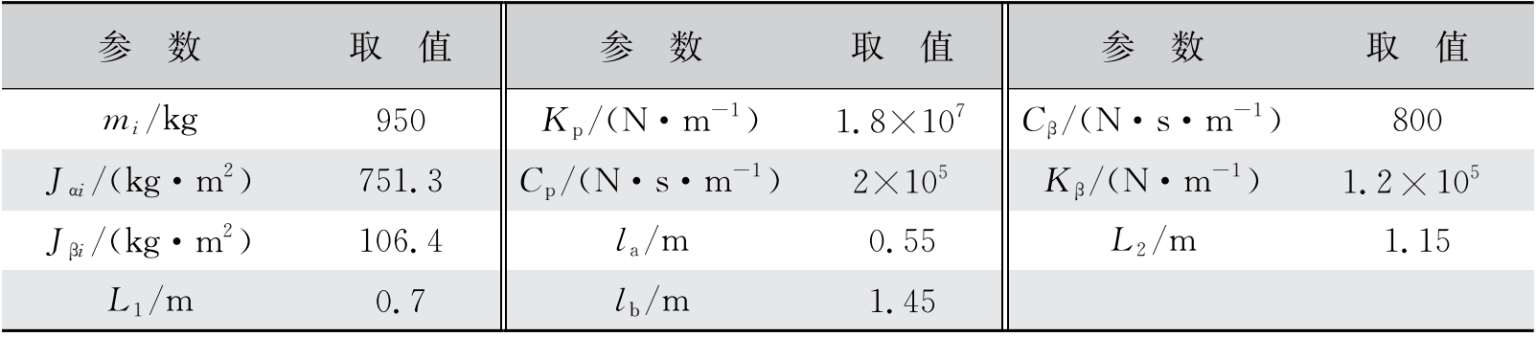
其中悬浮架单元动力参数见表2-1。
表2-1 悬浮架单元动力学参数
以第一位T形臂为例,其受力示意如图2-32所示。除重力外,T形臂还受到与车体铰接的约束反力、长拉杆约束反力和与移动滑台之间的作用力。
图2-32中的符号说明如下:
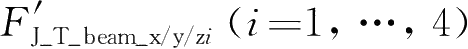 表示第
i
位T形臂与车体之间的x/y/z方向铰接约束反力;
表示第
i
位T形臂与车体之间的x/y/z方向铰接约束反力;
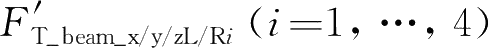 表示第
i
位长T形臂与纵向长拉杆之间的x/y/z方向作用力;
表示第
i
位长T形臂与纵向长拉杆之间的x/y/z方向作用力;
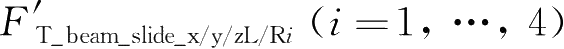 表示第
i
位长T形臂与滑台之间的x/y/z方向作用力。
表示第
i
位长T形臂与滑台之间的x/y/z方向作用力。
T形臂具有摇头一个自由度,因此其运动方程如下:
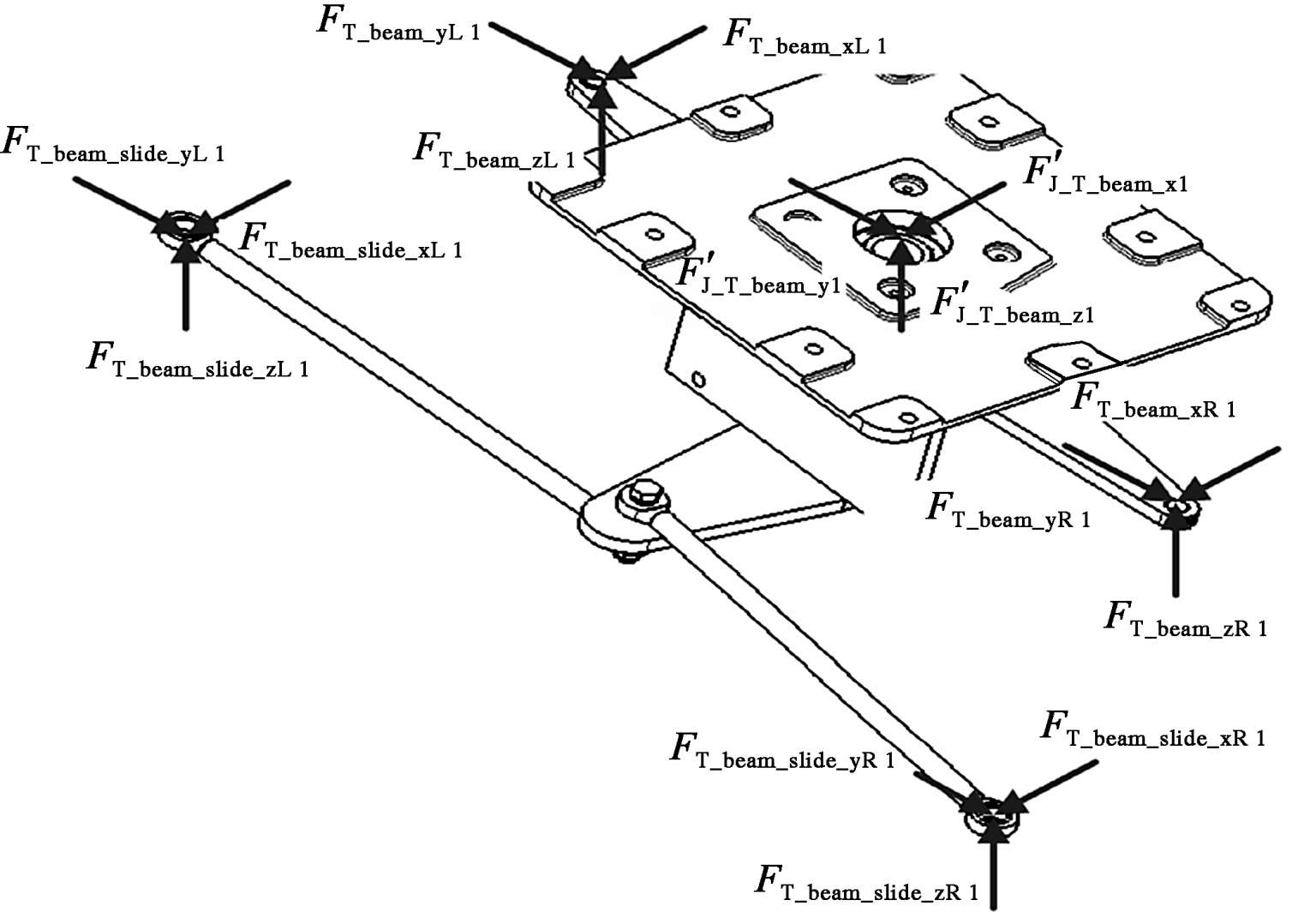
图2-32 纵向长拉杆及T形臂受力示意图
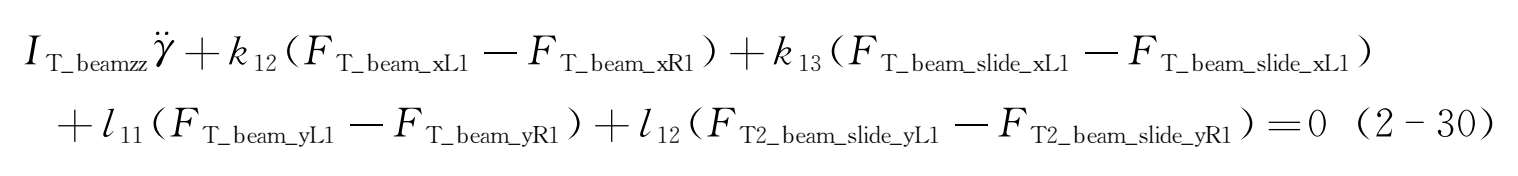
式中 I T_beamzz ——T形臂绕 z 轴的转动惯量;
l i , k i ——各作用力点与T形臂重心之间的 x 、 z 方向的距离。
由车辆各部件的受力和轨道车辆动力学理论可知,构架、车体是典型的多体系统,中低速磁浮车辆各刚体部件详细的运动自由度见表2-2,构架和车体具有6个自由度。车辆拓扑图如图2-33所示。
表2-2 各刚体模型的自由度
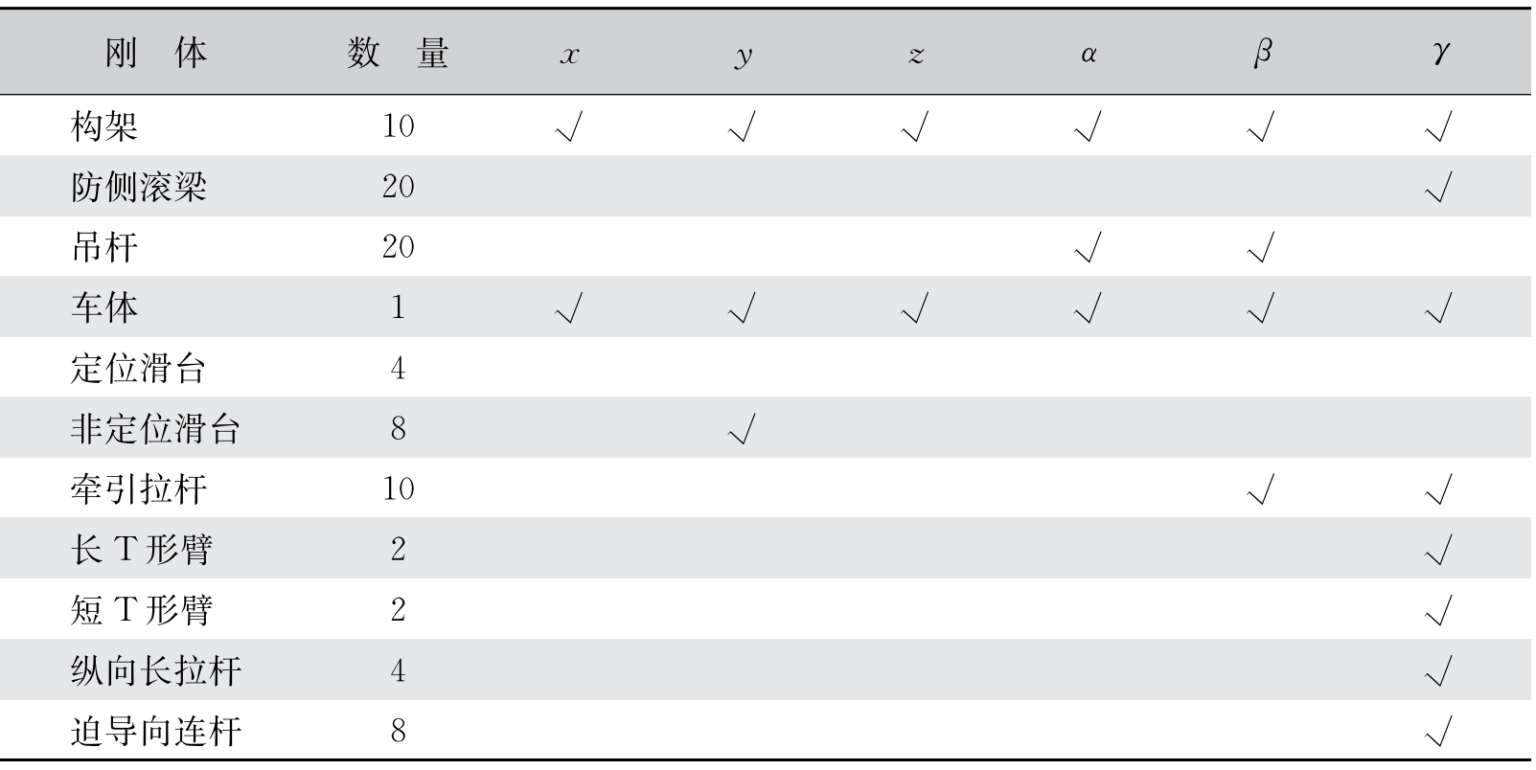
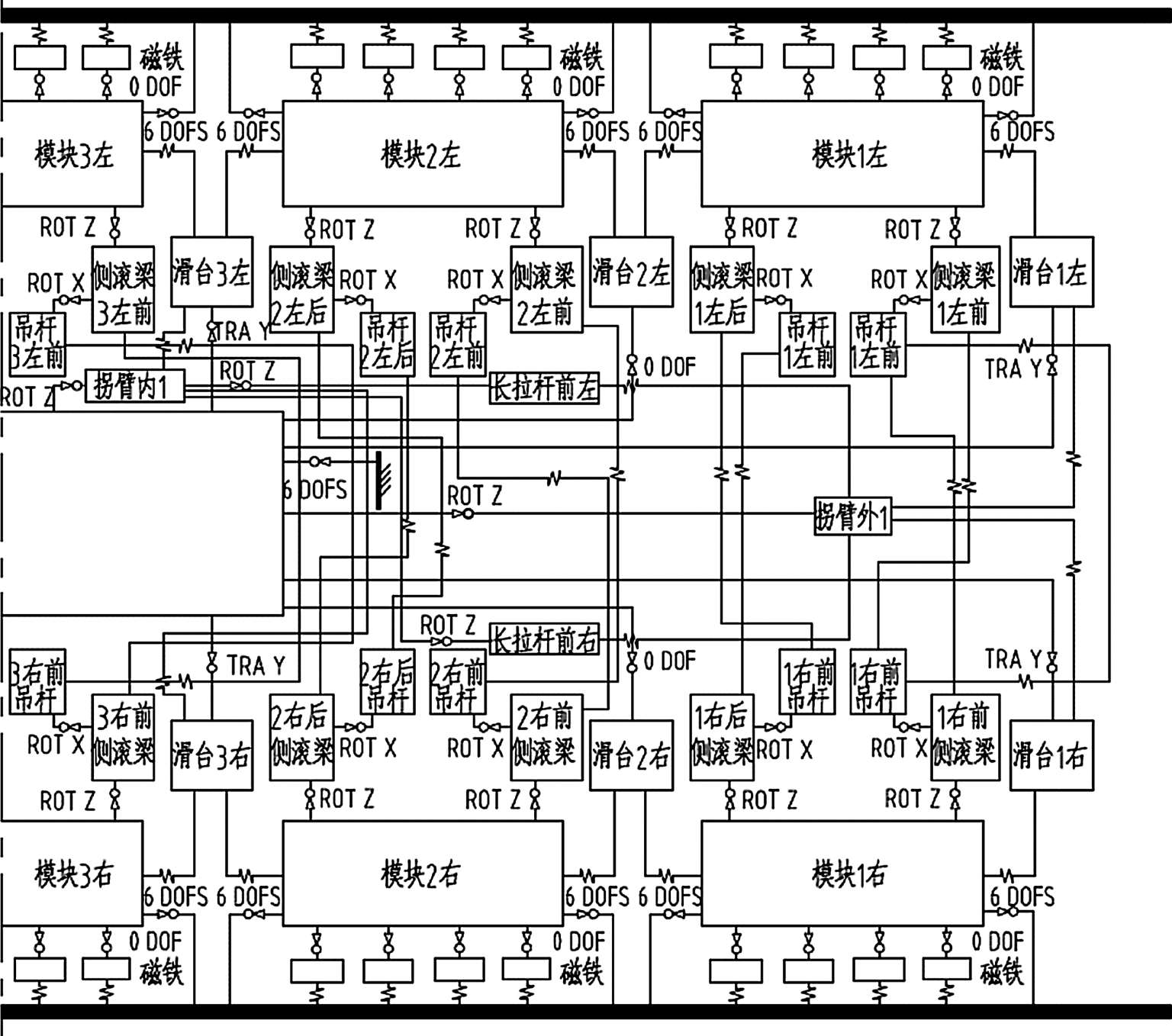
图2-33 车辆拓扑图
采用SIMPACK铁路模块建模,整个车辆建立在一个沿轨道前进且能反映轨道不平顺的移动平台上,每个走行机构有4对悬浮线圈,整车共有20对悬浮线圈,移动平台由20对假想移动点组成。模块通过悬浮控制等效弹簧元件支承在这20对假想移动点组成的移动平台上。
左、右模块抗侧滚建模与实际结构一致,因此抗侧滚梁和吊杆在模型中作为独立刚体处理。
车辆的迫导向机构建模与实际结构一致,但为了简化模型,迫导向机构中全部采用杆件来替代钢缆。
车辆的二系空气簧支承采用了垂向限位,以防止车辆过曲线时产生过度侧滚,影响曲线通过的平稳性和安全性,也可以加强车辆的抗侧风能力;为了保护空气簧不至于产生过大的水平变形,空气簧横向也采用了限位措施。
滑台是本车辆结构中的一个特殊部件,在其他轨道车辆中很少用到,滑台相对车辆仅有横向平移自由度,每个滑台支承在两个空气簧上(端部除外),而这两个空气簧又分别位于相邻的两个模块上,与实际结构相一致。