
下载掌阅APP,畅读海量书库
立即打开




由麦克斯韦方程组可以看出,激发电磁波的源是电荷密度 p 和电流密度矢量 J 。但在该方程组中,电场和磁场相互耦合,这给求解电磁波带来很大的不便。如果只将电场或磁场用源来表示成一个方程,会带来方便,这个方程实际上就是电磁场的波动方程。下面我们由麦克斯韦方程组导出电磁场的波动方程。
对于时谐电磁场,电磁场的波动方程为
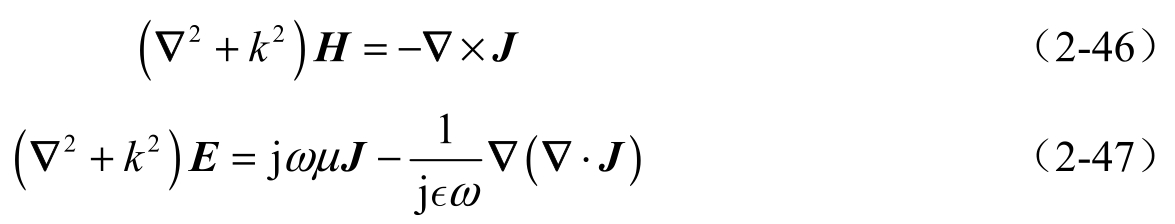
式中, k 为一个常数,通常称为波数,与波长和频率之间的关系有关。
在推导过程中,我们利用了时谐电荷守恒定律的表达式。对于只有磁荷存在时的波动方程可利用对偶关系获得,本节不再详述。
在无源区, J = 0, ρ= 0,电磁场的波动方程变为
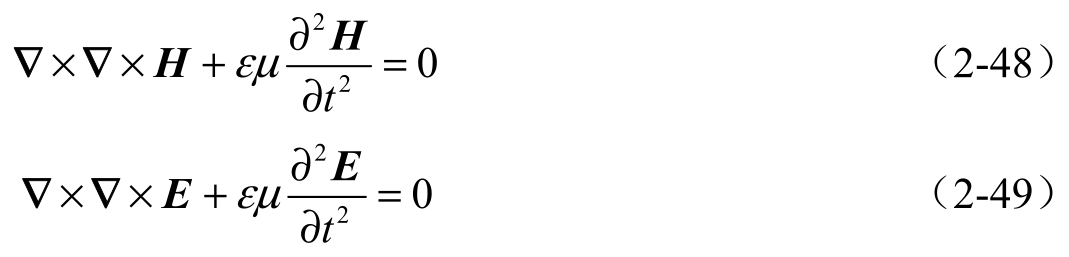
由以上的讨论可以看出,直接由场源的分布求解电磁场是十分复杂的,这是由于电流密度、电荷密度以相当复杂的形式出现在方程的右边,给直接求解电磁场带来了不便。为了简化电磁场的计算,通常会引入电磁位函数。电磁位函数有矢量位、标量位、赫兹矢量、德拜矢量等函数,较常用的电磁位函数为 A 、 φ 。