




到目前为止,我们学习了如何设计由一组彼此交互的对象所构成的系统,在对象的设计和交互上,要根据要解决的问题做适当的抽象。但我们还不知道如何创建这些抽象层。有很多不同的方法可以做到,我们将在第10、11和12章讨论一些高级的设计模式。大部分设计模式都依赖于两个基本的面向对象原则: 组合 与 继承 。组合的概念简单一些,所以我们从它下手。
组合是通过把几个对象收集在一起来生成一个新对象的行为。当一个对象是另一个对象的一部分时,组合通常是比较合适的选择。实际上,我们已经在上面机械师的示例中见识了组合过程。汽车是由发动机、传动装置、启动装置、车前灯、挡风玻璃及其他部件组成的,而发动机又是由活塞、曲柄轴和阀门等组成的。在这个示例中,组合是提供抽象的好办法。 Car 对象可以提供司机所需的接口,同时也能够访问内部的组件,从而为机械师提供适合他们操作的深层抽象。当然,如果机械师需要更多的信息来诊断问题或调节发动机,那么这些组成部分也可以进一步被细分。
这是一个常用的介绍组合概念的示例,但在设计计算机系统时它并不是特别有用。物理对象通常很容易被分解为零件对象。人们至少从古希腊时就开始这么做,提出了原子是物质最小的组成单位的假设(当然他们那时还没有粒子加速器)。因为计算机系统涉及很多特有的概念,把计算机系统分解成组件对象不像分解阀门和活塞那么自然。
面向对象系统中的对象偶尔也会代表物理对象,例如人、书或手机。但更多时候代表的是抽象的概念。人有名字,书有标题,手机用于打电话等。在物理世界中,我们通常不会把打电话、书的标题、人的名字、约会,以及支付等看作对象,但是在计算机系统中,它们通常会被建模为对象。
让我们试着模拟一个更加面向计算机的示例,从实践中学习组合的概念。我们将设计一个基于计算机的象棋游戏。这是20世纪80年代与20世纪90年代校园里非常流行的一个消遣活动。人们曾经预测在未来某一天计算机能够打败人类象棋大师。当这件事在1997年真的发生时(IBM的深蓝机器人打败了世界象棋冠军Gary Kasparov),人们对这个问题的兴趣渐渐淡去。现在,深蓝机器人的新版本总能打败人类。

象棋游戏( game )需要两个玩家( player ) 参与 ( play ),使用一个由8×8网格组成的64格( position )棋盘( board ),棋盘上包含两队各16枚( piece )可以 移动 ( move )的棋子,两个玩家各自以不同的方式轮流( take turn )移动棋子。每一枚棋子都可以 吃掉 ( take )另一枚棋子。玩家每走一步,棋盘必须在计算机显示器上重新 绘制 ( draw )自己。
在上面的描述中,我已经用楷体标记了一些可能的对象,用 粗体 标记了几个关键方法。通常这是从面向对象分析到设计的第一步。现在,我们把重点放在组合的概念上,先关注棋盘,不用太在意不同玩家和不同类型的棋子。
我们先从最高的抽象开始。我们有两个玩家(Player),他们和 Chess Set 交互,轮流下棋,如图1.7所示。

图1.7 象棋游戏的对象/实例图
这看起来不太像之前的类图,因为它确实不是类图。这是 对象图 ,又叫 实例图 。它描绘的是系统在某个特定状态下,对象实例之间的关系,而不是类的交互。图1.7中的两个玩家是同一个类的不同实例。相应的类图如图1.8所示。
这个类图表明,一盘象棋只能由2个玩家(Player)一起玩,而且任何一个玩家在某一个时间点上只能玩一盘 Chess Set 。

图1.8 国际象棋游戏的类图
我们现在的重点是组合概念,不是UML,所以我们考虑一下 Chess Set 是由什么组成的。我们暂时不关心Player是由什么组成的。我们可以假设Player有心脏、大脑以及其他器官,但这些与我们的模型无关。实际上,玩家可能是既没有心脏也没有生理上的大脑的深蓝机器人。
Chess Set由一个棋盘(board)和32枚棋子组成。棋盘又包含64个网格位置。你可能会说棋子不是Chess Set的组成部分之一,因为你可以用另一副棋的棋子替换这副棋的棋子。虽然这在计算机游戏中不大可能发生,但这个问题引出了一个概念: 聚合 ( aggregation )。
聚合和组合的概念非常相似,区别在于聚合对象可以独立存在。棋盘中的格子无法独立于棋盘存在,因为我们说棋盘和格子是组合关系。但是,棋子可以独立于棋盘存在(棋盘丢了,棋子还可以独立存在),我们说棋子和棋盘是聚合关系。
我们也可以从对象生命周期的角度区分聚合和组合:
· 如果外围对象控制相关(内部)对象的创建和销毁,那么组合更适合。
· 如果相关对象可以独立于外围对象创建,或者它的生命周期可以更长,那么聚合关系更适合。
同时,别忘了组合关系也是聚合关系,因为聚合是一种更广义的组合。任何组合关系一定也是聚合关系,但聚合关系不一定是组合关系。

现在,我们画出 Chess Set 组合类图,并给各个类添加表达组合关系的属性,如图1.9所示。
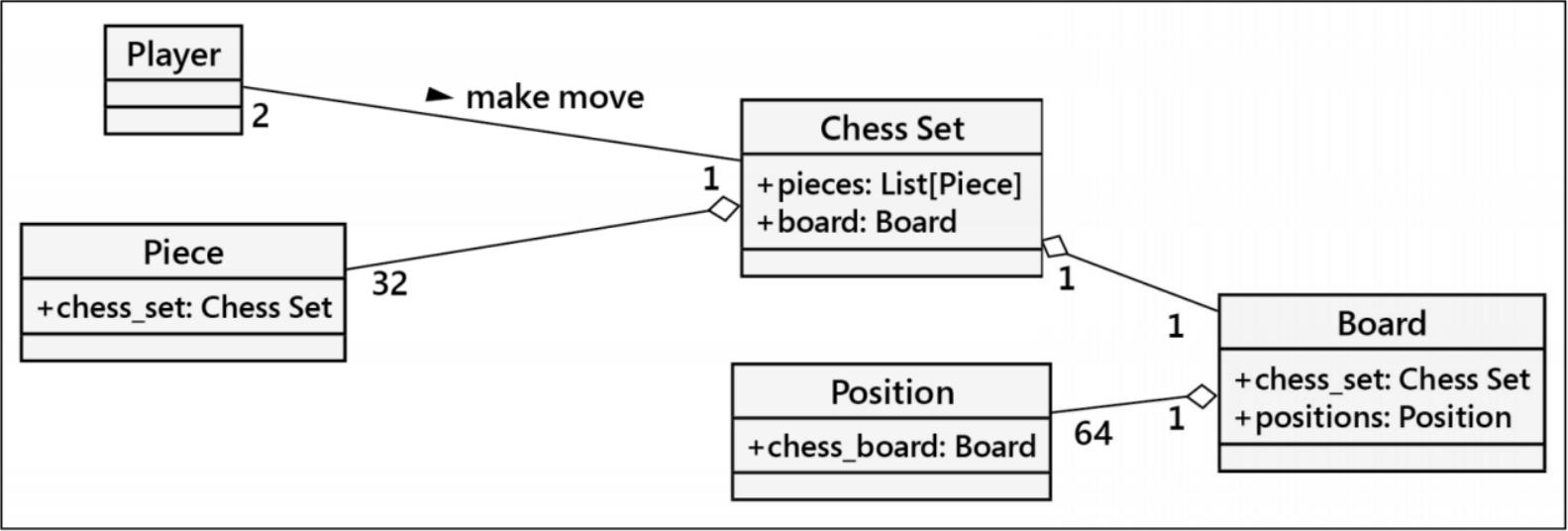
图1.9 象棋游戏的类图
组合关系在UML中用实心菱形表示,而空心菱形表示聚合关系。你会发现,棋盘(Board)和棋子(Piece)都是 象棋 ( Chess Set )的一部分,它们都是Chess Set类的属性。这再次说明,在实践中,聚合与组合的区别一旦过了设计阶段就变得无关紧要了。在实现阶段,它们的用法基本相同。
然而,在与团队讨论不同对象之间如何交互时,两者的区别还是很有帮助的。尤其是当讨论相关对象在内存中存活多久时,你将需要区分是组合还是聚合。在很多情况下,删除一个组合对象会同时删除关系中的相关对象,比如删除棋盘(Board)会同时删除棋盘上的所有格子。然而,删除一个聚合对象,不会自动删除关系中的相关对象。