




深度学习模型学习参数过程中,除了损失函数,还有一个必不可少的部分就是优化方法。深度学习算法的本质都是建立模型,通过优化方法对损失函数进行训练优化,找出最优的参数组合,也就找到了当前问题的最优解模型。在第4章会重点介绍各种优化方法,本小节主要介绍梯度下降法。
梯度下降法的优化思想在于用当前位置负梯度方向作为搜索方向,因为负梯度方向是当前位置损失函数的最快下降方向,因此也被称为“最速下降法”。如图2.9所示,为了方便演示,假定模型中只有一个参数
θ
,蓝色曲线为损失函数随着参数
θ
的变化情况,导数
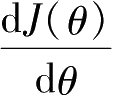 代表的是曲线某点处切线的斜率。损失函数的导数代表着参数
θ
变化时,损失函数
J
值相应的变化,如图中该点损失函数的导数为负值,故随着参数
θ
的增大,损失函数
J
减小。因此,导数也代表着一个方向,导数为正就对应着损失函数增大的方向,导数为负就对应着损失函数减小的方向。
代表的是曲线某点处切线的斜率。损失函数的导数代表着参数
θ
变化时,损失函数
J
值相应的变化,如图中该点损失函数的导数为负值,故随着参数
θ
的增大,损失函数
J
减小。因此,导数也代表着一个方向,导数为正就对应着损失函数增大的方向,导数为负就对应着损失函数减小的方向。
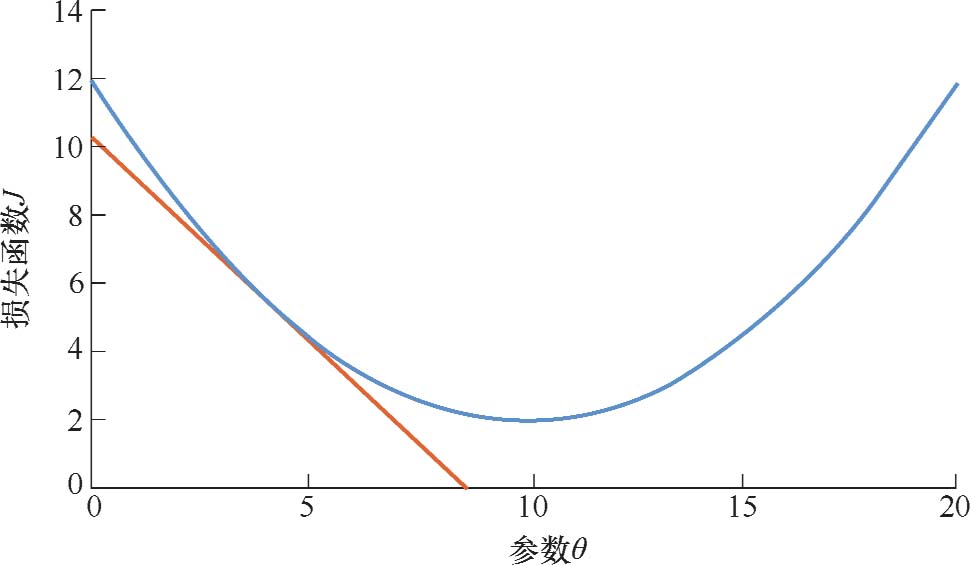
图2.9 损失函数及切线演示
标准梯度下降法(Batch Gradient Descent)参数更新公式为

式中, θ 为需要训练更新的参数; J ( θ )为损失函数;∇ θ J ( θ )为损失函数的梯度; α 为学习率。学习率 α 并非越小越好, α 太小会导致迭代速度过慢,为了减小损失函数,将会导致迭代次数较大,所需要的迭代时间就会非常长; α 也不能取得过大,否则容易导致参数 θ 在损失函数最小的区域附近反复振荡,最终导致模型收敛的结果并不是损失函数最小的点,如图2.10所示。
这和我们每个人的个人学习成长是类似的,每个人都需要不断迭代更新自己的知识和能力,但不能期望一口吃成大胖子,要逐步、持续地更新迭代,每次优化一点点,日积月累起来就能得到很大的提升。
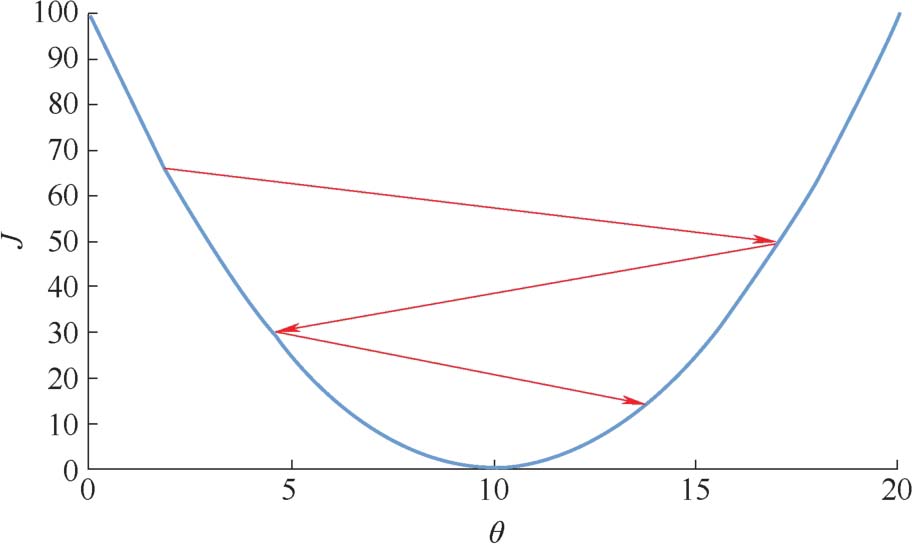
图2.10 学习率变化示意
梯度下降法的优点在于,若损失函数为凸函数,则一定能够找到全局最优解;若损失函数为非凸函数,则能够保证至少收敛到局部最优解。但是缺点是在接近最优解区域时收敛速度会明显变缓,因此利用梯度下降法来求解更新参数需要的迭代次数非常多。此外,标准梯度下降法是先计算所有样本汇总误差,然后根据总误差来更新参数,这种更新方式对于大规模样本问题的求解效率是相对很低的,因此提出了随机梯度下降法(Stochastic Gradient Descent):

与标准梯度下降法计算所有样本汇总误差不同,随机梯度下降法是随机抽取一个样本来计算误差,然后更新权重。随机梯度下降法是最小化每个样本的损失函数,尽管不是每次迭代得到的损失函数都是朝向全局最优,但是总体方向来讲是朝向全局最优的,并且由于在参数更新的过程中是在随机挑选样本,因此会有更多的概率跳出一个相对较差的局部最优解,再收敛到一个更优的局部最优解甚至全局最优解。总体来讲,随机梯度下降法比较容易收敛到局部最优解,但有时候容易被困在鞍点附近。因此结合标准梯度下降法和随机梯度下降法提出了小批量梯度下降法(mini-batch Gradient Descent):

mini-batch Gradient Descent每次训练都是从训练集中取一个子集(mini-batch)用于梯度计算,基于计算出的梯度进行参数更新。相较于前两种梯度下降方法,该方法的收敛速度比前两种都快,并且收敛较为稳定。当然它也有一些缺点,例如对学习率的选择较为敏感、需要使用较为合适的初始化数据和步长等,但是从整体性能上来看是优于前两者的。因此,现在使用梯度下降法往往都是指mini-batch Gradient Descent。