下载掌阅APP，畅读海量书库
立即打开
“西洋十五子棋”比“圈叉游戏”复杂得多，概率和策略均在游戏中起一定作用。这是一种古老的游戏，其变体可以追溯到几千年前，在历史上称为“桌游”。这款游戏的目标是根据抛掷两个骰子的结果在棋盘上移动棋子并最终将棋子从棋盘上拿下（两个骰子的点数分开算，因此掷出6和5后可以移动6个位置和5个位置，而不是一次移动11个位置）。如果对手的棋子是一个“点”（三角玩法位置的名称）上唯一的棋子，那么玩家可以拿下对手的棋子；但是，如果某点上已有对手的两个或更多棋子，那么玩家就不能在那个点上再放棋子。
影响策略的一个因素是抛掷两个骰子的可能结果。如上所述，7是概率最大的总点数（因为它可以由1+6、2+5、3+4、4+3、5+2和6+1组成）；表2-1中列出了其他总点数的概率：
表2-1 两个骰子总点数的概率
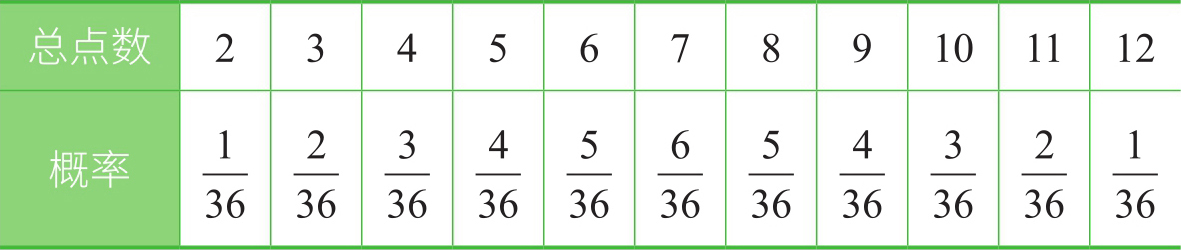
知道这一点会有用，因为可用的开局一招是将两个骰子的点数应用到同一个棋子上——因此，例如，您可以将一个棋子先移动6个位置，然后再移动5个位置，这样总共移动11个位置，如图2-4所示。尽管这种概率对比赛的结果很重要，但是它的重要性会因受阻点数而改变。游戏策略在很大程度上涉及对这些阻挡的处理，原因有二。首先，因为需要按照每个骰子上的数值单独移动，所以如果向前移动5个位置或向前移动6个位置没有受到阻挡，那么一个棋子只能移动11个位置（沿用上面的例子）。其次，当某玩家有一个或多个棋子被吃掉时，他在将该棋子（或多个棋子）放回棋盘之前不能采取任何其他行动。根据掷骰子的结果，棋子回到棋盘上玩家开始时的那
部位。因此，如果白方的某棋子被吃掉，而黑方挡住了该部位的某（几）点，那么白方就更难回来继续下棋。
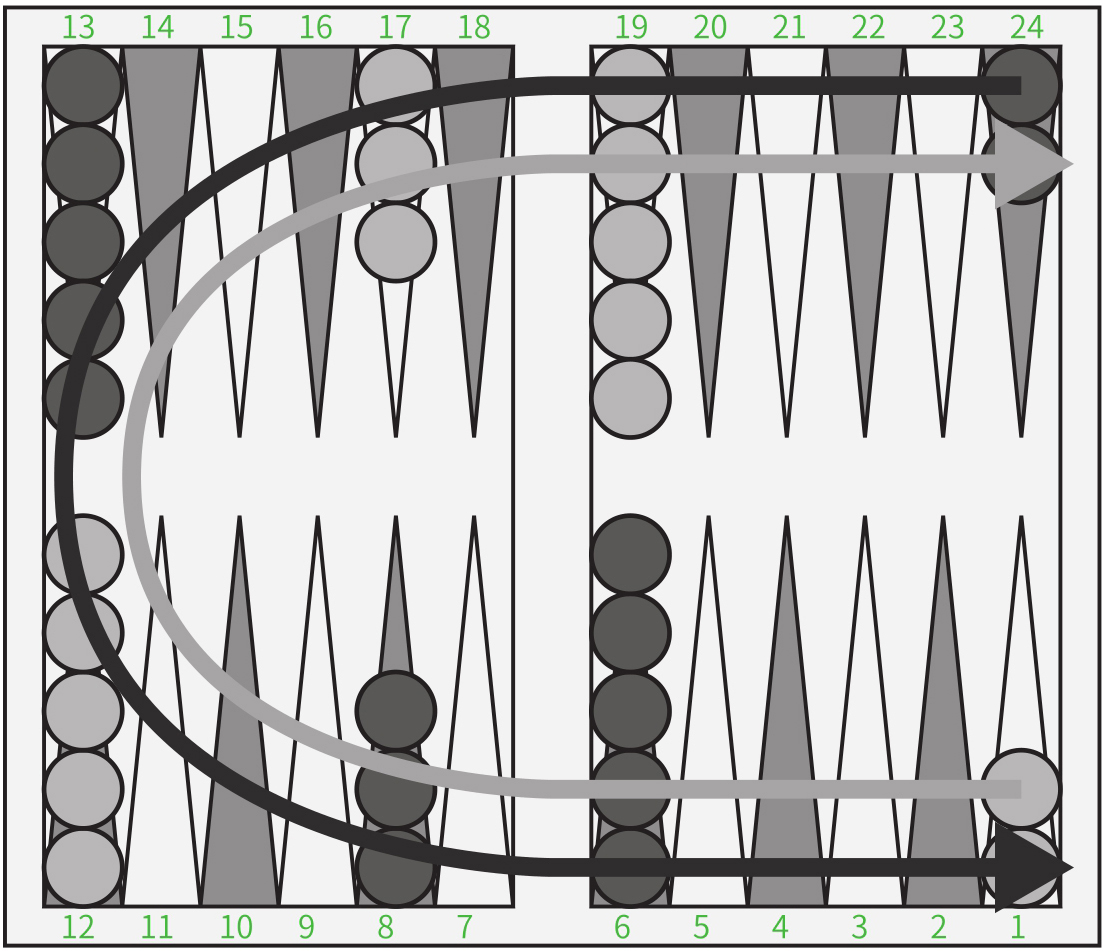
图2-4 “西洋十五子棋”开始位置，显示移动方向
“西洋十五子棋”策略的关键方面有多个，其中两个是游戏的开始和结束部分。用任何骰子组合来确定最佳的开局棋步都是可能的。例如，如果掷骰子的结果为5点和6点，那么有两个棋子的某点上的一个棋子应该移动到棋盘的另一端，而两个单独点数的许多组合（例如1和3或2和4）应该用于移动棋盘上被两个位置分开的一对棋子中的每一个棋子，从而挡住另外某点。
同样，当游戏结束时，玩家必须将所有棋子放入棋盘上自己那边的最后
，然后才能将棋子从棋盘上拿下。通常有两种选择：一种是短距离移动2个棋子，另一种是长距离移动1个棋子。如果2个棋子的移动能让玩家将2个棋子放到最后
，或者将2个棋子完全从棋盘上拿下，那么这是更好的策略，因为这样可能以更少的步数结束棋局。
虽然看起来很简单，但是“西洋十五子棋”棋盘上有大约10
17
个可能的位置组合，扩大策略范围的因素是游戏中“翻倍”的能力。默认情况下，赢得游戏后，玩家会获得一分（或货币单位）。如果某玩家在另一名玩家将棋盘上任何棋子拿掉之前完成游戏，那么该值将增加到2分（称为“大胜”）；如果某玩家完成游戏，而另一名玩家在棋盘上其第一个
部位还有至少一个棋子，那么该值将增加到3分（称为“全胜”）。
不过，在轮到自己时，任何一个玩家均有机会将游戏的数值翻倍。如果另一名玩家接受，那么赢家可以得到的点数翻倍——如果另一名玩家不接受，那么提供双倍点数的玩家立即获胜，获得游戏的当前数值。一旦一个玩家翻倍并得到接受，则只有另一个玩家可以翻倍——该权限在玩家之间来回传递。
翻倍通常被记录在“翻倍骰子”上——骰子的侧面有数字2、4、8、16、32和64。但是，翻倍的规则没有限制，而且可能重复拿掉棋子，重新设定棋子的位置，这意味着原则上游戏有无限的可能状态。（以上对可能位置数量的计算假设只有三种可能的翻倍状态，对应于无人翻倍、白方控制翻倍或黑方控制翻倍。）
与“圈叉游戏”相比，尽管“西洋十五子棋”不是纯粹策略性的，但是它确实可以利用数学概念来增强策略。