




图1.1展示了科赫雪花是什么样的。其左、右两部分的形状与中间那部分完全相同,只是规模更小。同理,中间那部分本身是由形状与其相同但规模更小的部分组成的。这就是分形的自相似重复特征。

图1.1 科赫雪花
只要知道如何计算构成科赫雪花的基本形状中的各个点,便可开发一种算法来递归地执行相同的计算,从而绘制出越来越小的基本形状,构建出科赫雪花这种分形。本节将首先概述递归的工作原理,然后研究如何利用递归、一些线性代数知识和Python模块turtle来绘制科赫雪花。
为对递归的工作原理有所认识,下面来看一个简单的递归算法:计算阶乘。阶乘可使用下面的函数定义:
f ( N )=1×2×3×…×( N −1)× N
换而言之, N 的阶乘就是整数1~ N 的乘积。对于上面的函数,可改写成下面这样:
f ( N )= N ×( N −1)×…×3×2×1
并进一步改写为下面这样:
f ( N )= N × f ( N −1)
上面使用 f 本身定义了 f 的阶乘,这就是递归。调用 f ( N )将导致调用 f ( N −1),进而导致调用 f ( N −2),以此类推。然而,在什么情况下停止递归呢?为此,需要将 f (1)定义为1,为递归指定终点。
下面演示如何使用Python来实现递归的阶乘函数:
def factorial(N):
❶ if N == 1:
return 1
else:
❷ return N * factorial(N- 1)在❶处,处理了N为1的情形——直接返回1;在❷处,实现了递归调用:调用函数factorial(),并传入参数N−1。这个函数将不断调用自身,直到N为1。这样做的效果是,当这个函数返回时,就计算出了整数1~N的乘积。
一般而言,实现使用递归的算法时应采取如下步骤。
1.定义一个基线条件(base case)。满足基线条件时,递归将终止。阶乘的基线条件是factorial(1)=1。
2.定义递归步骤。为此,需要考虑如何将算法表示为递归过程。在有些算法中,可能需要执行多次递归调用(稍后将介绍)。
解决可分解为其小型版本的问题时,递归是一个很有用的工具。可用于阶乘算法,也可用于科赫雪花的绘制。然而,递归并非总是效率最高的问题解决方式,在有些情况下,合理的选择是以循环的方式重新实现递归算法。但相比于循环实现,递归算法通常更紧凑、更优雅。
下面来看看如何构建科赫雪花。图1.2展示了用于绘制科赫雪花的基本图案,以下称之为片段(flake)。这个片段基于长度为 d 的线段 AB ,该线段被分为等长的3部分( AP 1 、 P 1 P 3 和 P 3 B ),其中每部分的长度都为 r 。 P 1 并非直接连接到 P 3 ,而是经由 P 2 连接到 P 3 。 P 2 是这样确定的: P 1 、 P 2 和 P 3 构成一个边长为 r 、高为 h 的等边三角形。点 C 为 P 1 和 P 3 之间的中点,它位于 P 2 的正下方,因此 AB 和 CP 2 是垂直的。
明白如何确定图1.2所示的各点后,就可递归地绘制越来越小的片段,从而构建出科赫雪花。大致而言,目标如下:给定点 A 和点 B ,需要计算点 P 1 、 P 2 和 P 3 的坐标,并像图1.2那样将它们连接起来。要计算这些坐标,需要使用一些线性代数知识,线性代数是数学的一个分支,能够根据向量计算距离以及确定点的坐标。所谓向量,指的是有长度和方向的量。
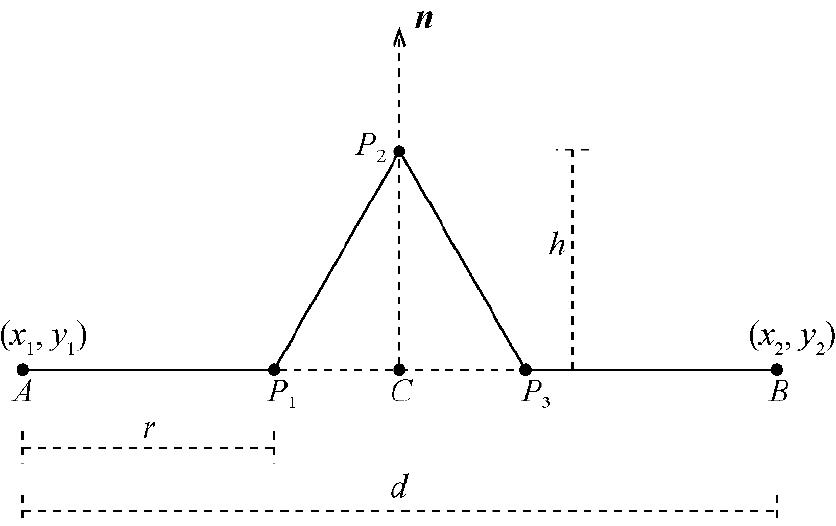
图1.2 用于绘制科赫雪花的基本图案
下面介绍一个简单的线性代数公式,后面将用到它。给定三维空间中的点 A 和单位向量 n (单位向量是长度为1的向量),要计算从点 A 出发沿这个单位向量移动距离 d 到达的点 B 的坐标,可使用下面的公式:
B = A + d × n
可通过示例轻松地验证这一点。假设点 A 的坐标为(5, 0, 0),单位向量 n 为(0, 1, 0),从点 A 出发沿这个单位向量移动10个单位到达点 B ,那么点 B 的坐标是多少呢?使用刚才的公式,可得到如下结果:
B =(5, 0, 0)+10×(0, 1, 0)=(5, 10, 0)
换而言之,要从点 A 到点 B ,需要沿 y 轴的正方向移动10个单位。
下面介绍另一个技巧,即垂直向量计算技巧(perpendicular vector trick)。假设有向量 A = ( a , b ),如果有另一个向量 B ,它与向量 A 垂直,那么可将它表示为向量 B = (− b , a )。要验证这个关系,可计算 A 和 B 的点积。要计算两个二维向量的点积,可将两个向量的第一个分量相乘,并将第二个分量相乘,再将这两个乘积相加。在这里, A 和 B 的点积如下:
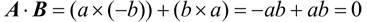
两个向量垂直时,它们的点积为0,因此 B 确实垂直于 A 。
掌握这些线性代数知识后,回过头来看图1.2所示的片段。给定点 A 和点 B 的坐标,如何计算点 P 2 的坐标呢?要到达点 P 2 ,可从点 C 出发,沿单位向量 n 移动距离 h 。根据前面的第一个线性代数公式可知:
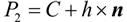
下面来将变量代入公式。点 C 为线段 AB 的中点,因此 C =( A + B ) / 2。其次, h 为边长为 r 的等边三角形的高。根据勾股定理可知:
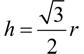
在这里, r 为点 A 到点 B 的距离的三分之一。如果点 A 的坐标为( x 1 , y 1 ),点 B 的坐标为( x 2 , y 2 ),可使用下面的公式计算它们之间的距离:
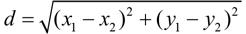
只需将这个公式的结果除以3,就可得到 r 的值。
最后,需要将向量
n
表示出来。假设
n
与向量
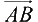 垂直,而向量
垂直,而向量
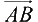 可表示为点
B
的坐标减去点
A
的坐标:
可表示为点
B
的坐标减去点
A
的坐标:
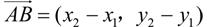
向量
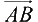 的长度
的长度
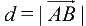 。现在利用前面的垂直向量计算技巧,使用
A
和
B
来表示
n
:
。现在利用前面的垂直向量计算技巧,使用
A
和
B
来表示
n
:
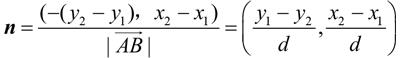
接下来需要计算 P 1 和 P 3 的坐标,为此需要用到另一个线性代数公式。假设有线段 AB ,而点 C 位于这条线段上;同时假设 a 为 A 到 C 的距离,而 b 为 B 到 C 的距离。可使用下面的公式来计算点 C 的坐标:
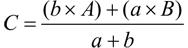
要明白这个公式,可假设点 C 为线段 AB 的中点,此时 a 和 b 相等。在这种情况下,凭直觉就能知道 C 的坐标应该为( A+B ) / 2。在上面的公式中,将所有的 b 都替换为 a ,结果如下:
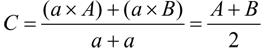
有了这个新公式后,就可计算 P 1 和 P 3 的坐标了。这两个点将线段 AB 三等分,这意味着 P 1 到 B 的距离为 P 1 到 A 的距离的两倍(即 b 1 =2 a 1 ), P 3 到 A 的距离为 P 3 到 B 的距离的两倍(即 a 3 =2 b 3 )。将这些值代入前面的公式,可得到如下计算 P 1 和 P 3 坐标的公式:
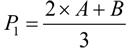
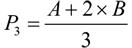
至此,就获得了绘制科赫雪花分形的第1层级所需的一切:给定点 A 和点 B ,然后通过计算确定点 P 1 、 P 2 和 P 3 。在这个分形的第2层级,将第1层级中片段内的每条线段(如图1.2所示)替换为更小的片段,结果如图1.3所示。
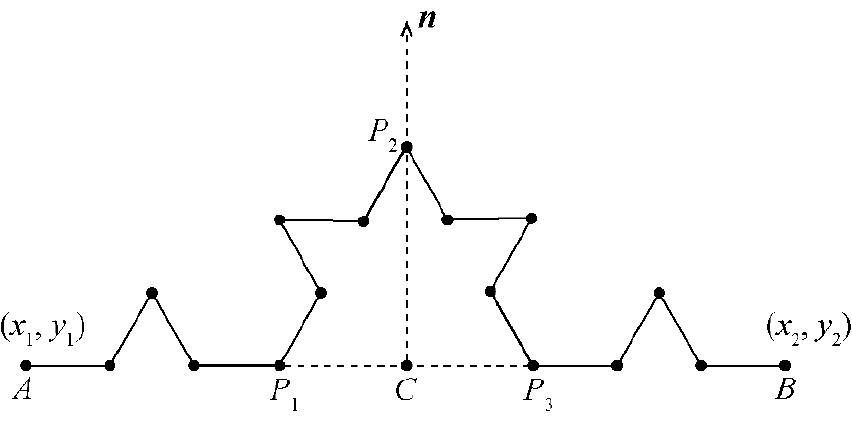
图1.3 构建科赫雪花的第2步
注意,对于图1.2所示的4条线段( AP 1 、 P 1 P 2 、 P 2 P 3 和 P 3 B ),以每条线段为基础构建了一个新片段。在绘制科赫雪花的程序中,将把每条线段的端点(如 A 和 P 1 )作为新片段的 A 和 B 的值,并递归地执行生成图1.2所示点的计算。
在分形的每个层级,都将再次对片段进行替换,从而绘制出越来越小的自相似图形。这就是科赫雪花绘制算法中的递归步骤,此后不断地重复这个步骤,直到满足基线条件。基线条件应该为线段 AB 的长度小于特定的阈值,如10像素。到达这个阈值后,将只绘制线段,而不再递归。
为让最终绘制出的科赫雪花更漂亮,可在分形的第1步绘制3个相连的片段,这样结果将更像雪花,呈六角对称,如图1.4所示。
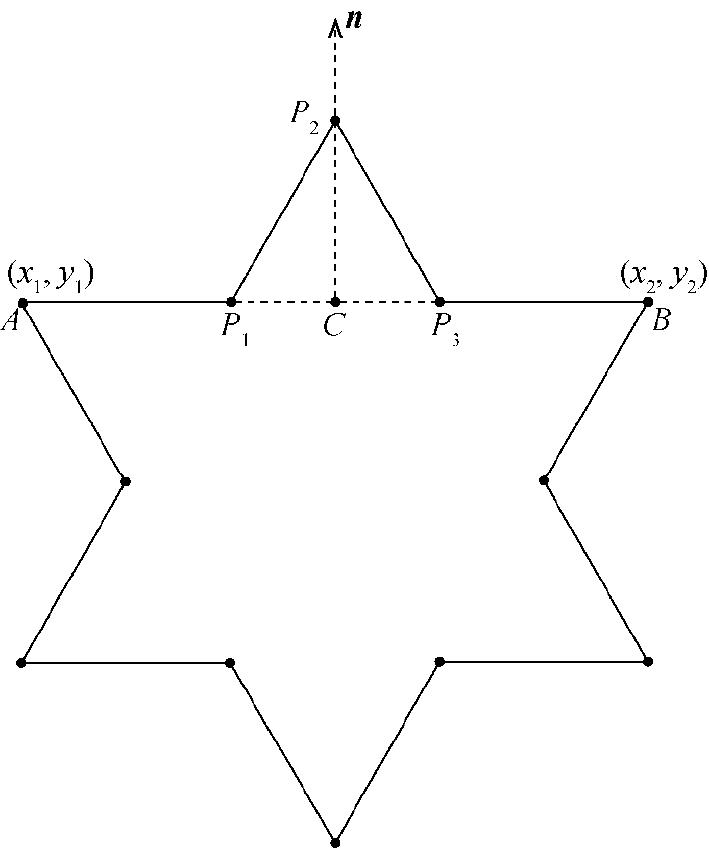
图1.4 合并3个片段
知道如何计算绘制科赫雪花所需的坐标后,下面来看看如何在Python中使用这些坐标来绘制图形。
为绘制科赫雪花,本章将使用Python模块turtle,这是一款简单的绘图程序,以海龟在沙滩上拖着尾巴前行为模型,绘制出各种图案。模块turtle包含用于设置画笔(相当于海龟的尾巴)位置和颜色的方法,还有很多有助于绘图的函数。
只需使用几个绘图函数就可绘制出科赫雪花。实际上,从turtle的角度看,绘制科赫雪花几乎与绘制三角形一样简单。为证明这一点,并初步讲解turtle是如何工作的,下面的程序使用turtle绘制了一个三角形。请输入这些代码,将其保存为test_turtle.py文件,再在Python中运行它。
❶ import turtle
def draw_triangle(x1, y1, x2, y2, x3, y3, t):
#尝试绘制一个三角形
❷ t.up()
❸ t.setpos(x1, y1)
❹ t.down()
t.setpos(x2, y2)
t.setpos(x3, y3)
t.setpos(x1, y1)
t.up()
def main():
print('testing turtle graphics...')
❺ t = turtle.Turtle()
❻ t.hideturtle()
❼ draw_triangle(-100, 0, 0, -173.2, 100, 0, t)
❽ turtle.mainloop()
# 调用main()函数
if __name__ == '__main__':
main()首先,导入了模块turtle❶。接下来,定义了方法draw_triangle(),其参数为3对坐标(三角形的3个顶点),以及turtle对象t。在这个方法中,先调用了up()❷,让Python抬起画笔,换而言之,就是让画笔离开虚拟纸张,以免在移动海龟时进行绘画。开始绘画前,需要指定海龟的位置。调用函数setpos()❸将海龟的位置设置为第1对坐标对应的点。调用函数down()❹将画笔放下,因此每次调用setpos()时,都相当于将海龟移到了下一组坐标处,进而绘制出一条线段。最终的结果为一个三角形。
接下来,声明了函数main(),实际的绘画工作是由它来完成的。在这个函数中,创建了用于绘画的turtle对象❺,并将其隐藏起来❻。如果没有隐藏turtle对象,将在绘制的线段开头看到一个海龟的图案。接下来,为绘制三角形,调用了draw_triangle(),并将所需的坐标作为参数传递给它❼。调用函数mainloop()❽确保绘制三角形后不会关闭tkinter窗口(tkinter是Python默认使用的GUI库)。
图1.5显示了这个简单程序的输出。
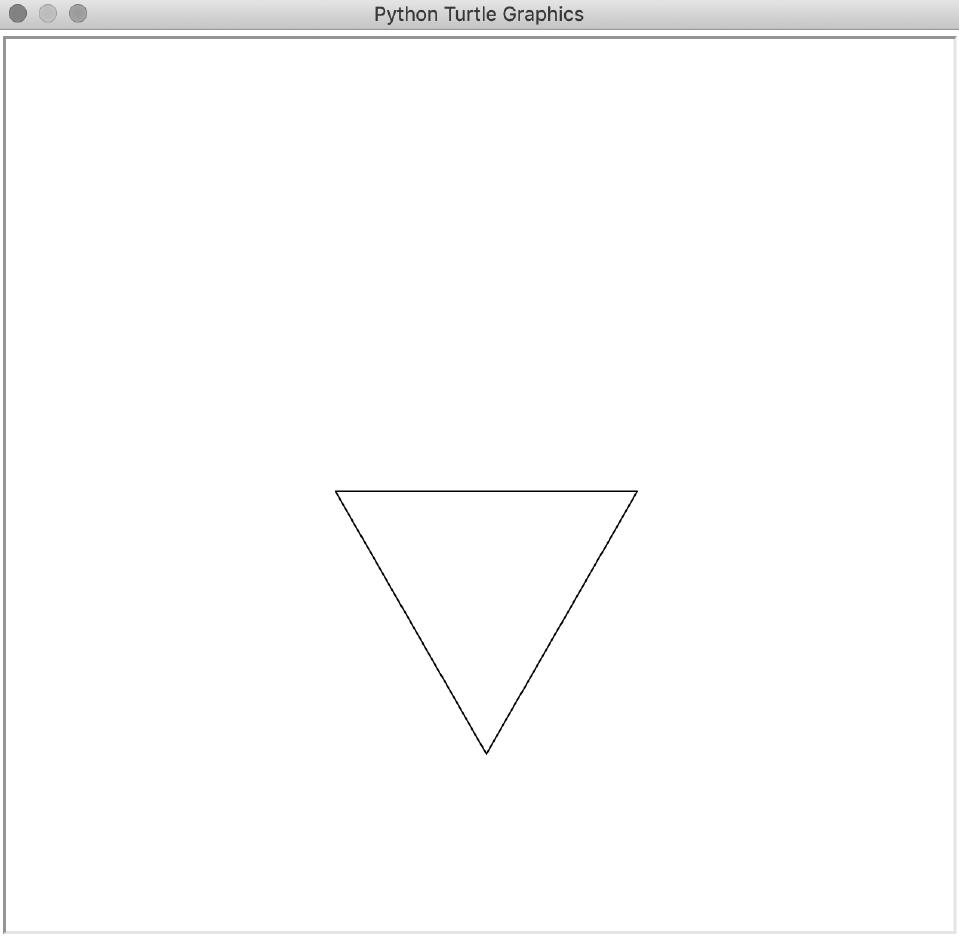
图1.5 使用海龟绘图法绘制三角形
有了完成本章项目所需的一切后,下面来绘制科赫雪花。