




运算放大器(运放)是布莱克(Black)的反馈放大器的现代版本。它是一个通用器件,广泛应用于仪器、控制和通信等领域。它也是模拟计算中的关键元件。运放及其两种表示符号如图4.7所示,它具有一个反相输入端( v - ),一个同相输入端( v + ),一个输出端( v out )。此外还有连接电源 e - 、 e + 的引脚,以及调零的引脚。假定输入电流 i - 和 i + 为零、且输出由以下的静态关系给定,即可得到一个简单的运放模型:
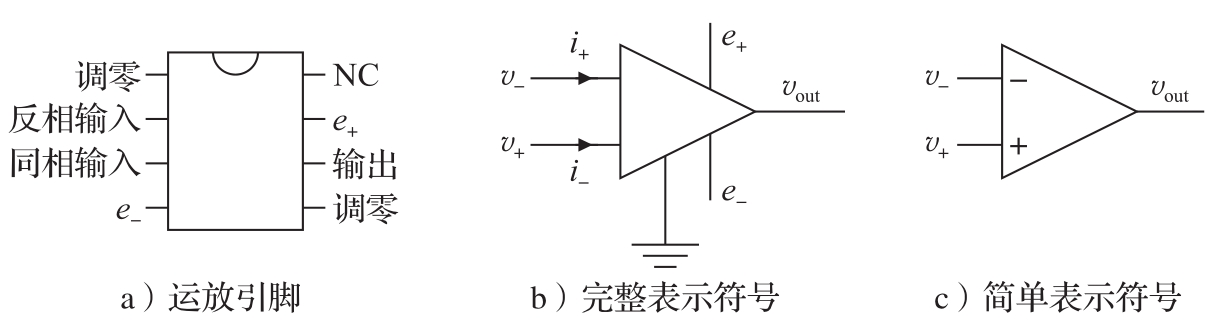
图4.7 运放及其两种表示符号
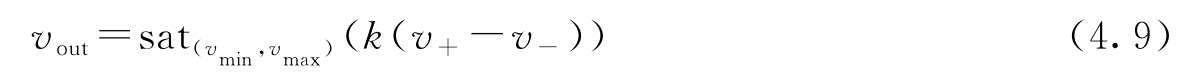
其中,
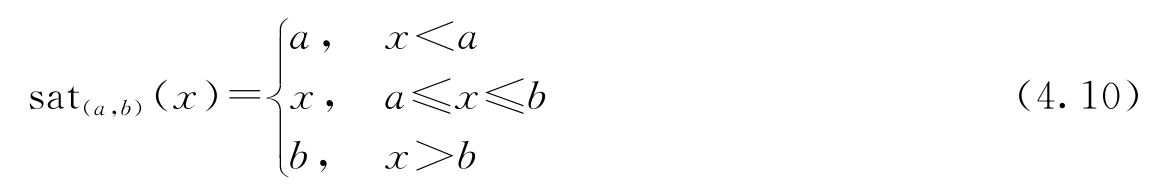
其中增益 k 很大(在10 6 ~10 8 的范围内),且电压 v min 和 v max 满足:
e -≤ v min < v max ≤ e +
即在供电电压的范围内。采用图4.8所示的平滑函数来代替饱和函数,可以得到更精确的模型。对于小输入信号,式(4.9)的放大器特性是线性的:
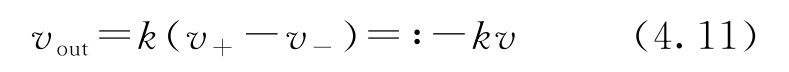
由于开环增益 k 特别大,使系统处于线性状态的输入信号范围相当小。
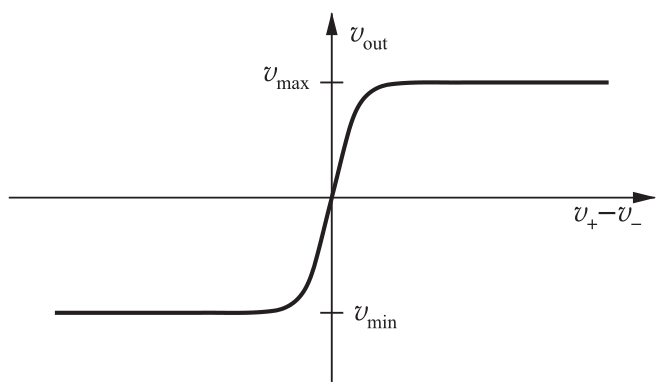
图4.8 运放的输入/输出特性。差分输入为 v + -v -。 在0附近的小范围内,输出电压是输入的线性函数(饱和值为 v min 和 v max )。在线性工作区,运放具有很高的增益
围绕基本的运放配置反馈,可以得到一个简单的放大器,如图4.9a所示。为了对该反馈放大器的线性区进行建模,假定电流 i 0 = i -+ i + 为零,且放大器的增益特别大,以致电压 v = v - v + 也为零。这样一来,根据欧姆定律可以得到流过电阻 R 1 和 R 2 的电流为:
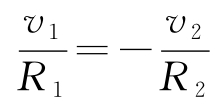
因此放大器的闭环增益为:
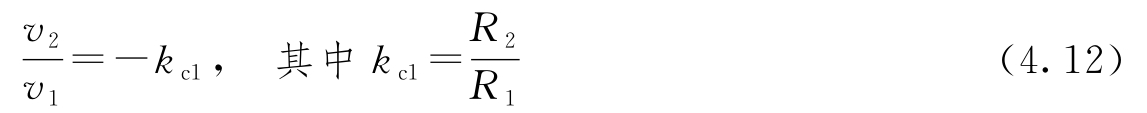
仍忽略电流 i 0 ,假定电压 v 虽小但不为零,可以得到一个更精确的模型。这时电流平衡为:

假定放大器运行在线性区,令式(4.11)中 v out = v 2 ,可得闭环系统的增益为:
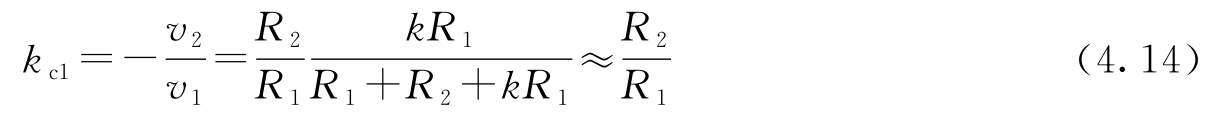
如果运放的开环增益 k 很大,则闭环增益 k cl 跟式(4.12)的简单模型给出的相同。请注意闭环增益仅仅取决于电路中的无源器件,且 k 的变化对闭环增益的影响很小。例如,若 k =10 6 , R 2 / R 1 =100,那么 k 变化100%所引起的闭环增益变化仅为0.01%。灵敏度如此大幅的降低很好地说明了用反馈可以从参数存在不确定性的器件制造出精确度很高的系统。在这个例子中,由于反馈的使用,实现了高增益、低鲁棒性和低增益、高鲁棒性之间的折中。正是式(4.14)给了布莱克(Black)发明反馈放大器的灵感 [45] (请参见第13章开篇的引文)。
给图4.9a所示的反馈放大器建立框图是有指导意义的。为此,将具有输入 v 和输出 v 2 的单纯放大器表示为一个方块。为了完成框图,还要对 v 与 v 1 和 v 2 之间的依赖关系进行描述。从式(4.13)求解 v 可得:
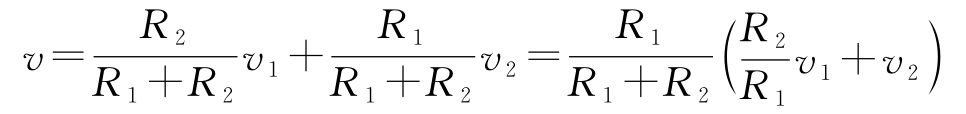
由此得到如图4.9b所示的原理框图。该原理图清楚地表明,这个系统存在反馈,且从 v 2 到 v 的增益为 R 1 /( R 1 + R 2 ),这也可以从图4.9a的电路图中得到。如果回路是稳定的,且放大器的增益很大,那么误差 e 就很小,因此有 v 2 =-( R 2 / R 1 ) v 1 。请注意电阻 R 1 同时出现在框图的两个方块中。这种情况在电路中很常见,这正是框图有时不能很好地适用于某些物理建模的原因之一。
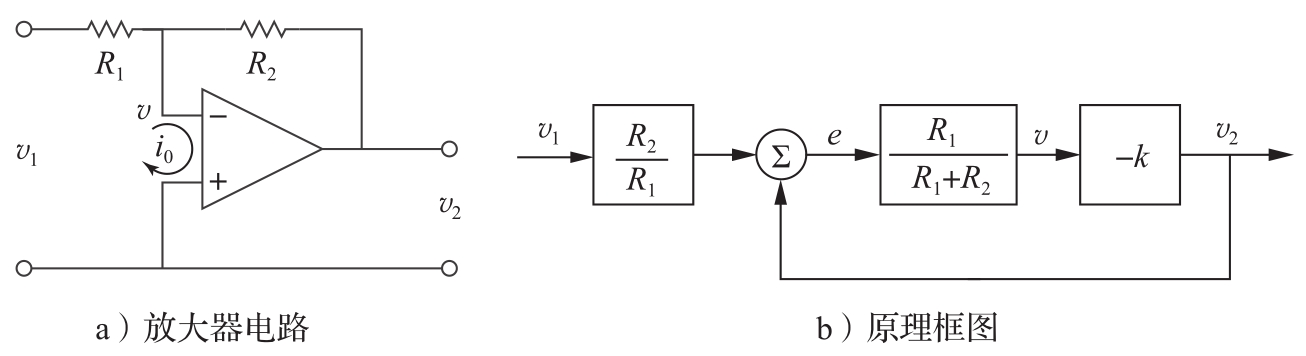
图4.9 采用运放的稳定放大器。图a的电路采用了运放的负反馈连接,图b是其原理框图。电阻 R 1 和 R 2 决定放大器的增益
式(4.11)所给的放大器简单模型为我们提供了定性认识,但其忽略了放大器也是动态系统这个事实。以下是一个更接近实际的模型:

式中,参数 b 具有频率的单位,称作放大器的 增益-带宽积 (gain-bandwidth product)。是否要使用更为复杂的模型,完全取决于所要解决的问题以及不确定性柠檬图的大小。式(4.15)的模型仍然不适用于很高的频率和很低的频率,因为在低频下漂移会引起偏差,而在接近于 b 的频率时则会出现额外的动态行为。该模型既不适用于大信号的情况——供电电压构成了信号的上限,通常在5~10V的范围;也不适用于特别低的信号——因为存在着电气噪声。当然,如果需要,也可以加入这些特征,但会增加分析的复杂性。
运放的用途非常广泛,它与电阻、电容结合在一起,可以做出各种不同的系统。事实上,任何线性系统都可以用运放与电阻、电容的组合来实现。习题4.4展示了如何实现二阶振荡器,图4.10展示了一个由运放加反馈构成的PI控制器的电路图。
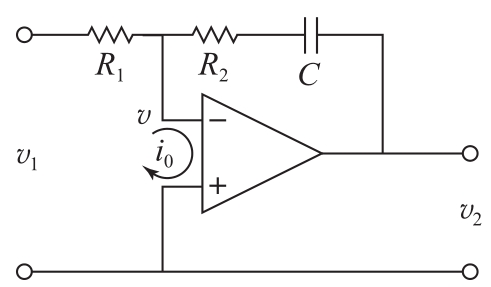
图4.10 由运放加反馈构成的PI控制器的电路图。电容用于存储电荷,表示输入的积分
为了建立该电路的简单模型,假定电流 i 0 为零,且开环增益 k 足够大,使得输入电压 v 可以忽略。通过电容的电流 i = C d v C /d t ,其中 v C 是电容两端的电压。由于流过电阻 R 1 的是同一个电流,因此可得:
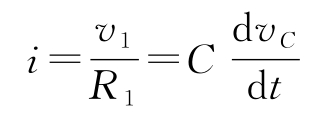
这意味着:
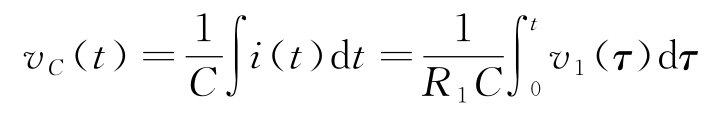
因此输出电压为:
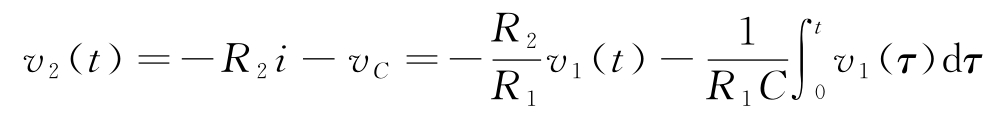
这就是PI控制器的输入/输出关系。
菲尔布里克(Philbrick)是开发运算放大器的先驱(见文献[170,201]),运放的应用有大量的教科书介绍(例如文献[65])。此外,从供货商处也可以得到很有用的信息(见文献[133,176])。