




3.1 (积分器链型)考虑线性常微分方程(3.7)。证明:选择状态空间表示为 x 1 = y ,则动态方程可以写成:
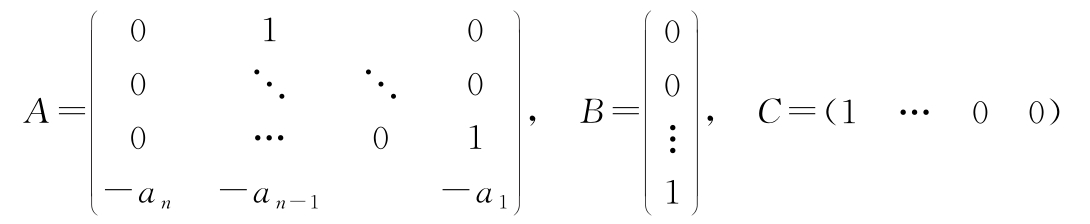
这个标准型称作 积分器链 (chain of integrator)型。
3.2 (离散时间动态)考虑下面的离散时间系统:
x [ k +1]= Ax [ k ]+ Bu [ k ], y [ k ]= Cx [ k ]
其中,
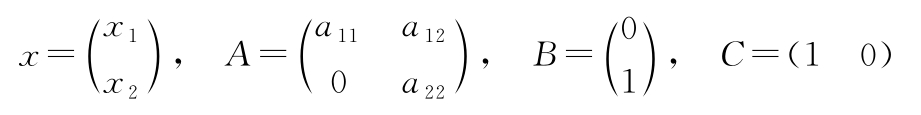
下面研究这个离散时间系统的一些特性随参数、初始条件及输入变化的函数关系。
(a)对于 a 12 =0、 u =0的情况,写出系统输出的闭式(或单一)表达式。
(b)一个离散系统,若对于所有
k
都有
x
[
k
+1]=
x
[
k
],则该离散系统处于
平衡点
(equilibrium)。假定
u
=
r
是一个恒定输入,请计算所得系统的平衡点。证明:若对于所有的
i
,都有
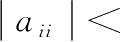 1,那么所有初始条件对应的解都将收敛于平衡点。
1,那么所有初始条件对应的解都将收敛于平衡点。
(c)编写计算机程序,绘制系统对单位阶跃输入 u [ k ]=1( k ≥0)的响应。绘制响应曲线时,请使用初始条件 x [0]=0, A 的元素取为 a 11 =0.5、 a 12 =1、 a 22 =0.25。
3.3 (凯恩斯经济学)一个经济系统的简单凯恩斯模型为:
Y [ k ]= C [ k ]+ I [ k ]+ G [ k ]
式中, Y 、 C 、 I 和 G 分别是第 k 年的国民总产值(GNP)、消费、投资及政府开支。消费和投资采用以下的差分方程建模:
C [ k +1]= aY [ k ], I [ k +1]= b ( C [ k +1] -C [ k ])
式中, a 和 b 为参数。第一个方程意味着消费随GNP增长,但存在滞后效应;第二个方程意味着投资正比于消费的变化率。
请证明:GNP的平衡点数值为
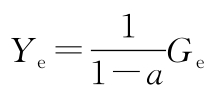
式中,参数1/(1 -a )是凯恩斯乘子(即从 G 到 Y 的增益)。当 a =0.75时,政府的一份支出将带来GNP的四份增长。另外,请证明:该模型可以写成以下的离散时间状态模型:
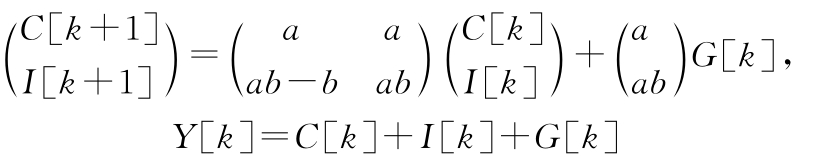
* 3.4 (最小二乘系统辨识)考虑以下的非线性微分方程:
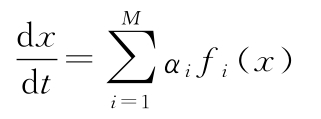
式中, f i ( x )是已知的非线性函数, α i 是未知的恒值参数。假定已经拥有整个状态 x 在 t 1 , t 2 ,…, t N ( N > M )等时间点上的测量值(或估计值)。请证明:通过求解以下形式的线性方程的最小二乘解,即可估算参数 α i 的值:
Hα = b
式中, α ∈ℝ M 是所有参数构成的向量, H ∈ℝ N × M 、 b ∈ℝ N 都具有恰当的定义。
3.5 (归一化的振荡器动态)考虑以下有阻尼的弹簧-质量系统的动态:
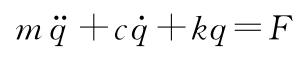
设
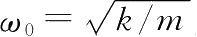 为自然振荡频率,
为自然振荡频率,
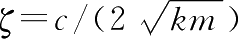 为阻尼比。
为阻尼比。
(a)证明:通过对该方程重新标度,动态方程可以写成以下形式

式中, u = F / k 。这个方程就是自然振荡频率为 ω 0 、阻尼比为 ζ 的线性振荡器的动态方程。
(b)证明:该系统可以进一步归一化成以下形式
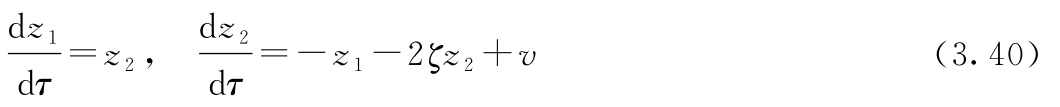
该系统的基本动态由单个阻尼参数 ζ 控制。有时用 Q 值(Q-value, Q =1/2 ζ )来代替 ζ 。
3.6 (Dubins car模型)证明:以后轮中心为参考点的车辆轨迹可以建模为以下的动态模型:
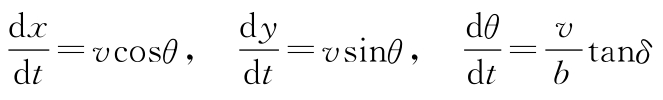
其中变量和常量的定义同例3.11。
3.7 (电气传动)考虑下图所示的系统,其中由扭簧连接的两个质量块由一台电动机驱动。
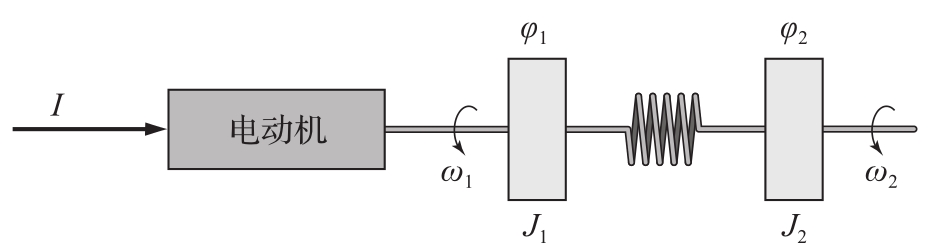
该系统可以代表电动机通过柔性轴驱动负载。假设电动机提供的转矩与电流 I 成正比,系统的动态可以用以下方程来描述
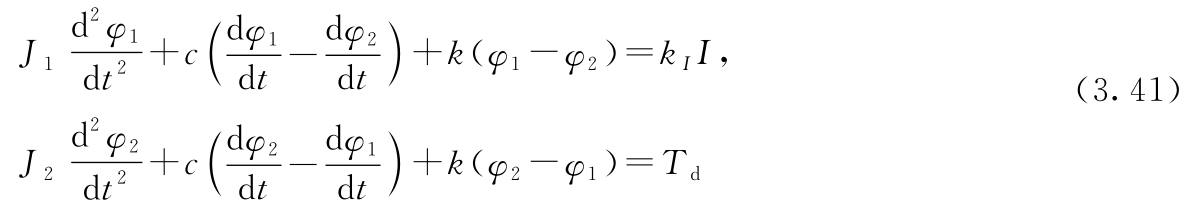
式中, φ 1 和 φ 2 是两个质量块的角位置; ω i =d φ i /d t 是它们的速度; J i 为转动惯量; c 为阻尼系数; k 为轴刚度; k I 是电动机的转矩常数; T d 是施加在轴端的干扰转矩。对于具有柔性臂的机器人、DVD和光盘臂的驱动,也可以得到类似的方程。
请通过引入归一化的状态变量
x
1
=
φ
1
,
x
2
=
φ
2
,
x
3
=
ω
1
/
ω
0
,
x
4
=
ω
2
/
ω
0
(其中
ω
0
=
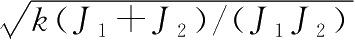 为控制信号为零时系统的无阻尼自然频率),推导系统的状态空间模型。
为控制信号为零时系统的无阻尼自然频率),推导系统的状态空间模型。
3.8 (发电机)连接到电网的发电机可以用发电机转子的功率平衡方程来建模:
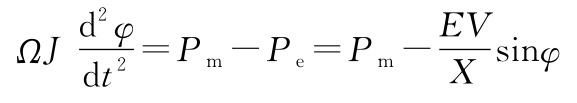
式中, Ω 是转子的机械角速度,可近似看成常数; J 是发电机的有效转动惯量; φ 是旋转角; P m 是驱动发电机的机械功率; P e 是发出的有功功率; E 是发电机的电压; V 是电网电压; X 是线路的电抗。假定电路的动态过程比转子的动态过程快得多, P e = VI =( EV / X )sin φ ,其中 I 是与电压 E 同相位的电流分量, φ 是电压 E 和 V 之间的相位角。试证明:发电机的归一化动态模型跟支点受力的单摆的归一化动态模型具有相同的形式。
3.9 (排队的准入控制)考虑例3.15所述的排队系统。在队列变得较大时,临时过负荷引起的长时延可以通过拒绝请求来减小。这样可以使已被接收的请求尽快得到满足,而得不到满足的请求则能够尽快收到拒绝信息以便它们可以尝试其他的服务器。考虑以下准入控制系统:
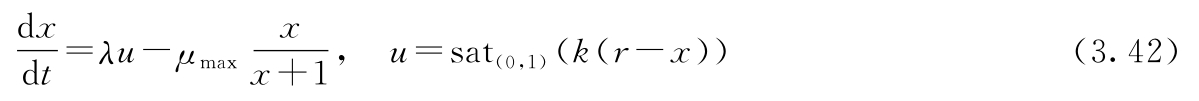
这里的控制器为带饱和的简单比例控制,饱和函数sat ( a , b ) 由式(4.10)定义, r 是期望的队列长度(参考值)。请证明:这个控制器可以降低高峰时间效应。并解释 r 的选择如何影响系统的动态。
3.10 (生物逻辑开关)如下图所示,将两个抑制子连接成一个环,可以构成一个基因开关。
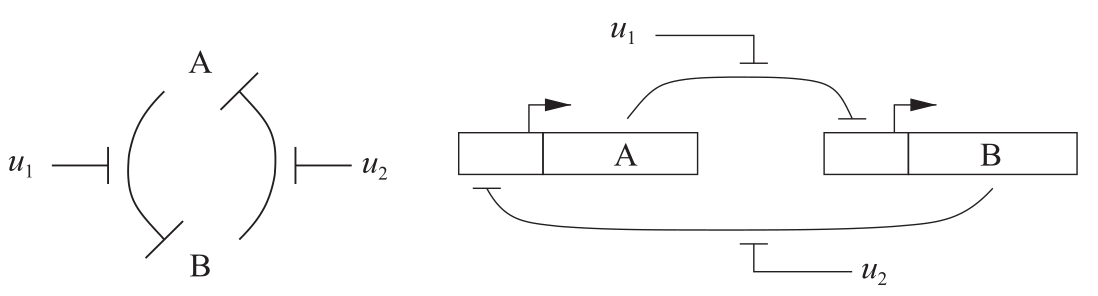
利用例3.18的模型——假定两个基因的参数相同,且mRNA的浓度能够快速达到稳定状态,证明:其动态可以写成以下归一化的形式
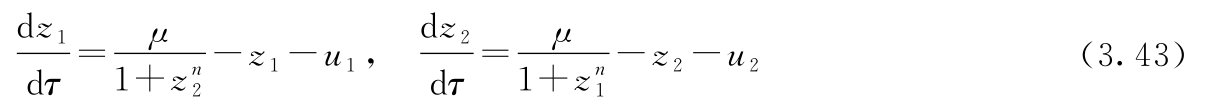
式中, z 1 和 z 2 是经过标度的蛋白质浓度,此外时间的比例也做了改变。证明:对于例3.18中的参数,可得 μ ≈200。并用仿真说明系统的类开关行为。
3.11 (FitzHugh-Nagumo方程)二阶FitzHugh-Nagumo方程
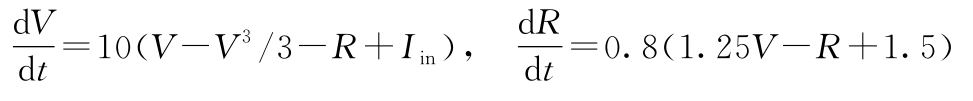
是例3.19中讨论的Hodgkin-Huxley方程的简化版本。其中变量 V 是穿过轴突膜的电压, R 是一个辅助变量,它近似表示流过轴突膜的好几个离子电流的影响。仿真以上方程,重现图3.28中的仿真结果。探讨输入电流 I in 的影响。
[1]
本书中,向量
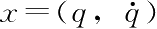 等价于向量
等价于向量
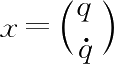 。
。
[2]
严格来讲,
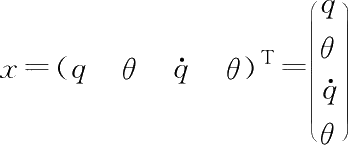 。
。