




要处理大型、复杂的系统,最好对系统进行不同的表示,以捕获系统的基本特征而隐藏不相关的细节。在所有的科学和工程分支中,常用的做法是采用系统的某些图形描述,即原理图(schematic diagram)。图形描述的范围很广,可以是风格各异的图片,也可以是大大简化的标准符号。这些图片既可以给出系统的全貌,又可以辨识单个的元件。图3.13给出了这种原理图的一些例子。原理图之所以有用,是因为它们在给出系统全貌的同时,还能显示出不同的子过程、它们之间的互联,并指示出可以调节的变量和可以测量的信号。
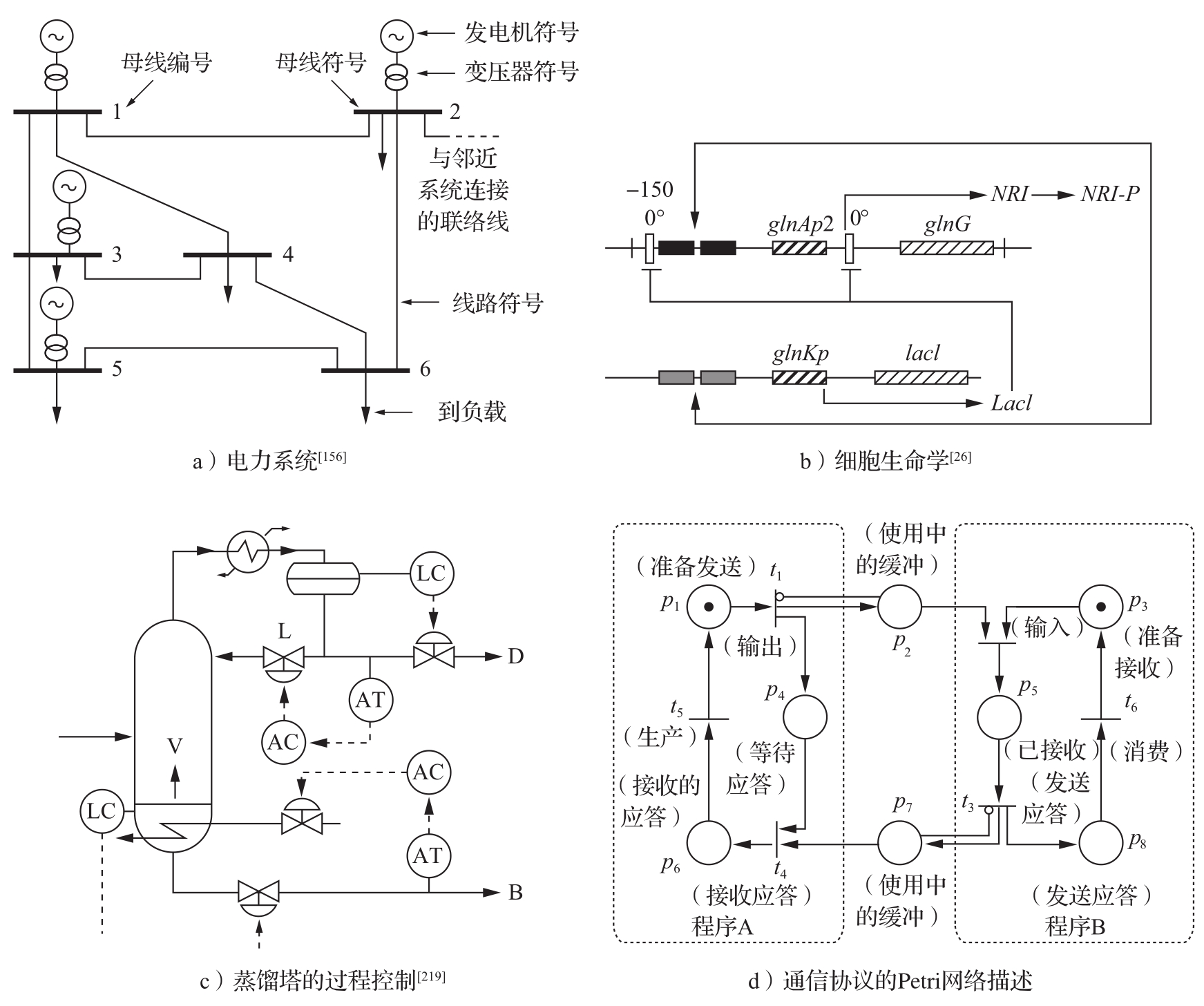
图3.13 不同学科的原理图
有一种特殊的图形表示称作框图(block diagram),它是在控制工程中发展起来的。使用框图的目的是突出信息流而隐藏系统的细节。在框图中,各种过程元素被显示为方块,每个方块拥有输入(以箭头指向方块的线段表示)和输出(以箭头离开方块的线段表示)。输入是指那些影响过程的变量,输出则是指我们感兴趣的那些信号或影响其他子系统的那些信号。框图也可以组成层次结构,其中单个方块本身又可以包含更详细的框图。
图3.14所示是框图中使用的一些符号。信号用线条表示,箭头指明输入和输出。图3.14a代表对两个信号求和。输入/输出响应用方块表示,并将系统的名字(或数学描述)写在方块中。有两种特别的情况,一个是比例增益,它将输入乘以一个放大系数,另一个是积分器,它对输入信号进行积分。
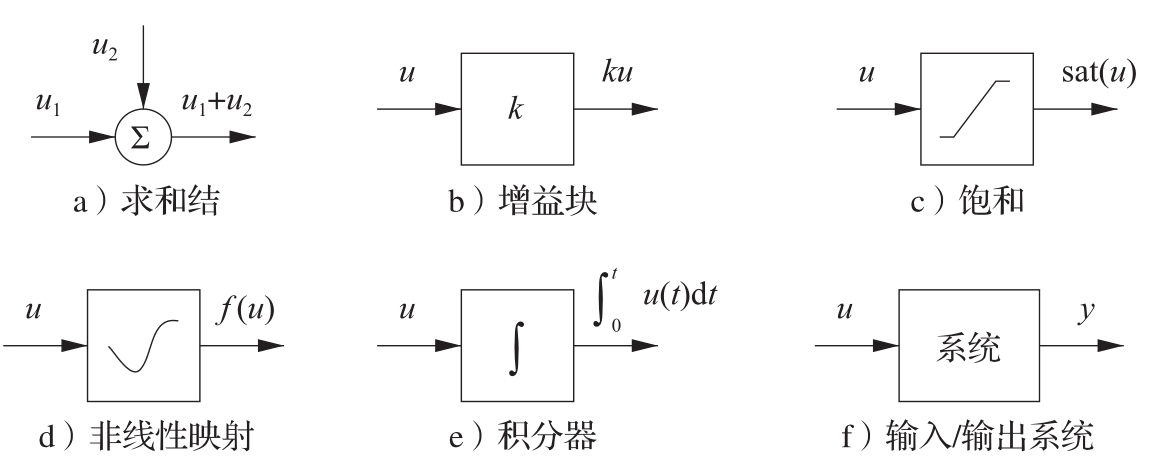
图3.14 标准框图的元件。箭头指明每个元件的输入和输出,相应的数学运算则标在元件的输出上。图f所示的系统方块元件表示一个动态系统的全部输入/输出响应
图3.15用于说明框图的应用,这里对昆虫(苍蝇)的飞行响应进行了建模。昆虫的飞行动态十分复杂,对苍蝇来讲,这牵涉到肌肉的仔细协调,以对外部激励进行响应,从而维持稳定飞行。苍蝇的一个已知特性是,它们利用其复眼的光流量构成反馈机制,因而具有顶风飞行的能力。粗略地讲就是,苍蝇控制自己的方向,以使视野收缩点位于其视野的中央 [207] 。
为了理解这个复杂行为,可以将整个系统的动态分解成一系列互联的子系统(或方块)。参照图3.15,可以用具有5个方块的互联系统来对昆虫的巡航系统进行建模。感官运动系统(a)利用来自视觉系统(e)的信息,产生肌肉指令,以图控制苍蝇,来使收缩点对中。这些肌肉指令通过翅膀空气动态(b),转换为驱动力。来自翅膀的驱动力与作用在苍蝇上的空气阻力动态(d)组合在一起,构成作用在苍蝇身体上的合力。风速通过空气阻力动态方块起作用。身体动态(c)则描述了苍蝇的平移和旋转运动与所受合力之间的函数关系。最后,昆虫的位置、速度和方向被反馈到空气阻力动态方块以及视觉系统方块,作为它们的输入。
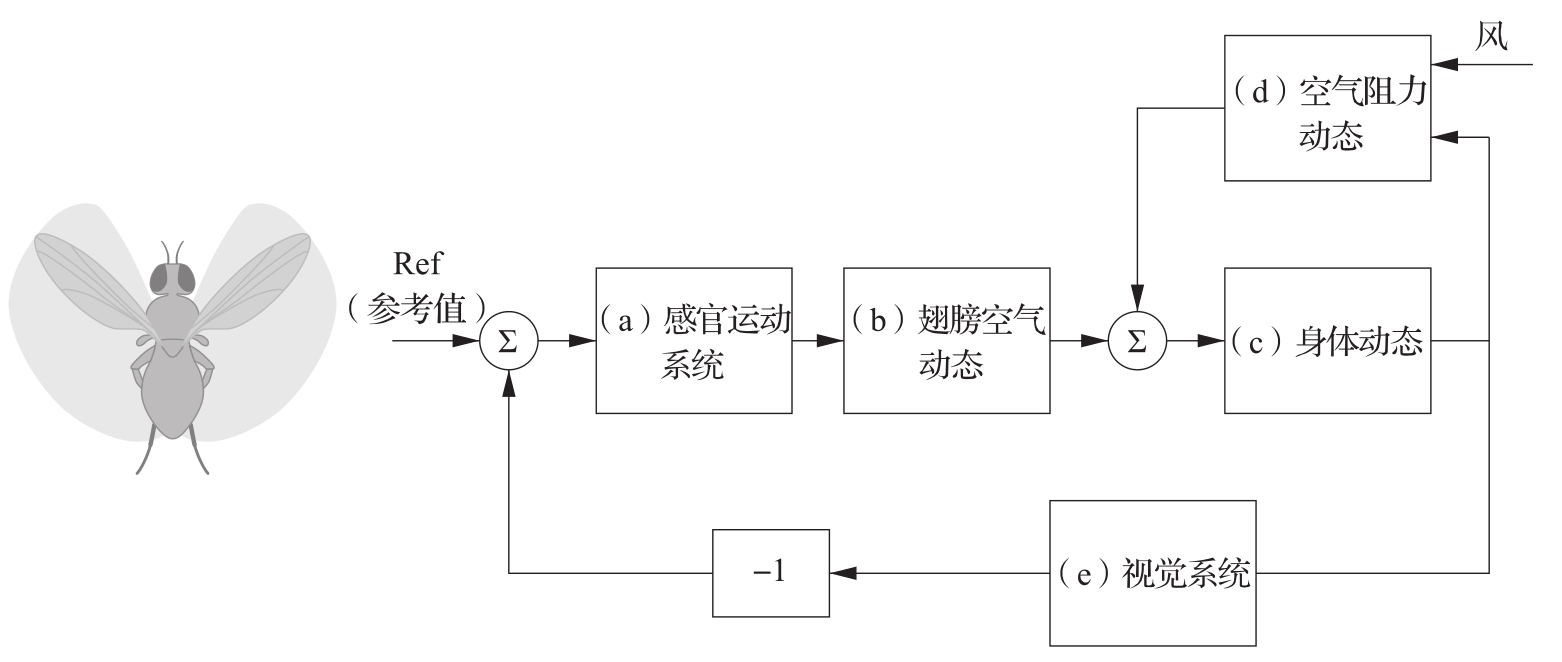
图3.15 逆风飞行的昆虫飞行控制系统的框图表示。模型的力学部分由苍蝇的刚体动态、在空气中飞行的阻力和翅膀扇动产生的力等组成。身体的运动引起苍蝇的视觉环境变化,这个信息被用于控制翅膀的运动(通过感官运动系统),从而形成闭环
图中的每个方块本身又可以是一个复杂的子系统。例如,果蝇的视觉系统由两个复杂的复眼组成(每个眼睛大约有700个元件),感官运动系统大约有200000个神经元用于处理信息。更详细的昆虫飞行控制系统框图应该将这些元件间的相互连接显示出来,但我们这里仅使用了一个方块来表示苍蝇的运动对视觉系统输出的影响,并使用另一个方块来表示苍蝇大脑如何处理视野以产生肌肉指令。框图详细程度的选择以及何种元件该进一步划分成不同的框图,往往都取决于经验以及需要用这个模型去解答的问题。框图的一个强大特征是,它们可以隐藏那些对于系统本质动态的理解没有关系的系统细节信息。
在对用框图描述的系统进行分析或仿真时,需要先建立描述整个系统的微分方程。在许多情况下,可以将描述各个子系统的微分方程结合起来,并进行一些变量代换来得到整个系统的方程。但当系统中存在这样的闭环子系统,其输入和输出之间存在正向的直接连接和反馈直接连接时,即存在 代数环 (algebraic loop)时,上述简单的处理方法就不能用了。所谓 直接连接 (direct connection),是指输入 u 的变化会导致输出 y 的立即变化。
为了了解其中的原委,考虑一个包含两个模块的系统,其中一个模块为一阶非线性系统:

另一个模块为比例控制器,方程为 u = -ky 。由于函数 h 不依赖于 u ,因此没有直接连接。在这种情况下,只需简单地将式(3.21)中的 u 用 -ky = -kh ( x )来代替,就可以得到闭环系统的方程:
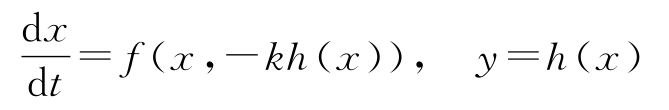
这是一个常微分方程。
如果存在直接连接的话,情况则会变得更为复杂。如果 y = h ( x , u ),那么用 -ky 代替 u 可得:
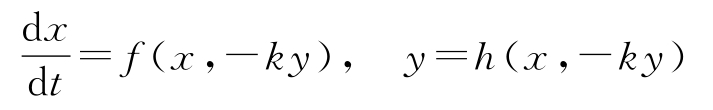
这里就存在代数环,为了获得 x 的微分方程,必须先从代数方程 y = h ( x , -ky )中解出 y =( x ),这通常是一项很复杂的任务。
当存在代数环时,就必须先求解代数方程来获得整个系统的微分方程。得到的模型是类似式(3.4)的微分方程组。代数环的消除不是一件容易的事情,因为这需要对代数方程进行符号求解。大多数基于框图的建模语言无法处理代数环,它们只能简单地给出存在代数环的提示。在模拟计算机的年代,通过在环路中引入快速动态环节能够消除代数环,然而这将产生病态的微分方程,其解具有快速分量和慢速分量,很难进行数值处理。像Modelica一类的高级建模语言则采用一些先进的方法来消除代数环。
由于控制系统拥有传感器和执行器,因此有可能通过对过程进行实验来获得系统动态的模型。但这种模型仅限于输入/输出模型,因为实验只能触及这些信号,不过实验建模也可以与采用反馈和互联的物理建模组合使用。
确定系统动态的一个简单办法是观测其对控制信号的阶跃变化做出的响应。在这个实验中,先要将控制信号设置为某个常数。当输出稳定到一个定值时(假设系统是稳定的),将控制信号迅速切换到一个新的数值并观测输出。这个实验给出的是系统的阶跃响应,响应曲线的形状给出了有关系统动态的信息。从响应曲线可以马上看出响应的时间、系统是否振荡、响应是否单调变化,等等。
考虑3.1节的弹簧-质量系统,其动态方程为:

为了确定常数 m 、 c 以及 k ,给系统施加一个幅值为 F 0 的阶跃输入,测量其响应。
在第7章将证明,当 c 2 <4 km 时,该系统在静止配置下的阶跃响应为:
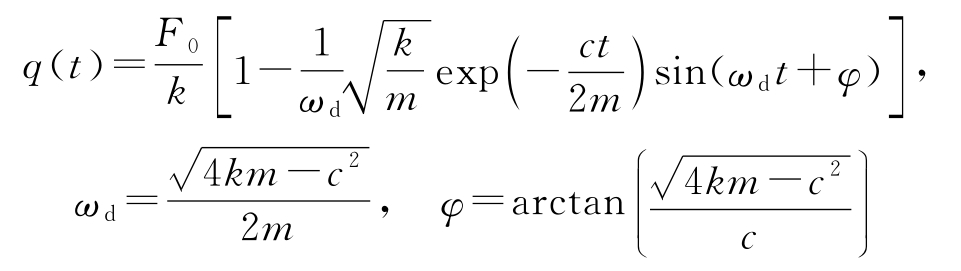
从以上解的形式可见,阶跃响应的形状是由系统的参数决定的。因此,通过测量阶跃响应的某些特征,可以确定参数的值。
图3.16给出了该系统对幅值为 F 0 =20 N的阶跃输入的响应,并标出了一些需测量的参数。首先可以注意到质量的稳态位置(在振荡消失之后)是弹簧常数 k 的函数:

式中, F 0 是所施加外力的幅值(对于单位阶跃输入, F 0 =1)。参数1/ k 称为系统的 增益 (gain)。振荡周期可以由两个峰值间的距离测得,它必须满足:
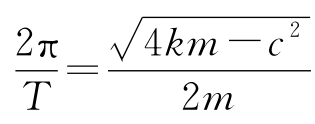
最后,振荡的衰减速率由解中的指数因子确定。测量两个峰值间的衰减量,可得:
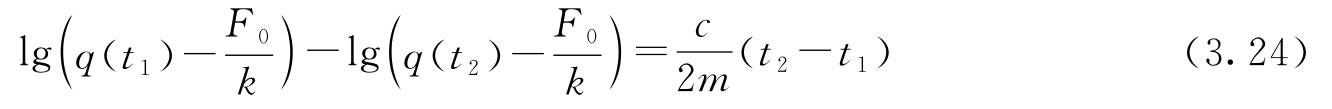
利用以上三个方程构成的方程组,可求解参数。对于图3.16所示的阶跃响应,可以确定出参数为 m ≈250 kg, c ≈60 N·s/m, k ≈40 N/m。
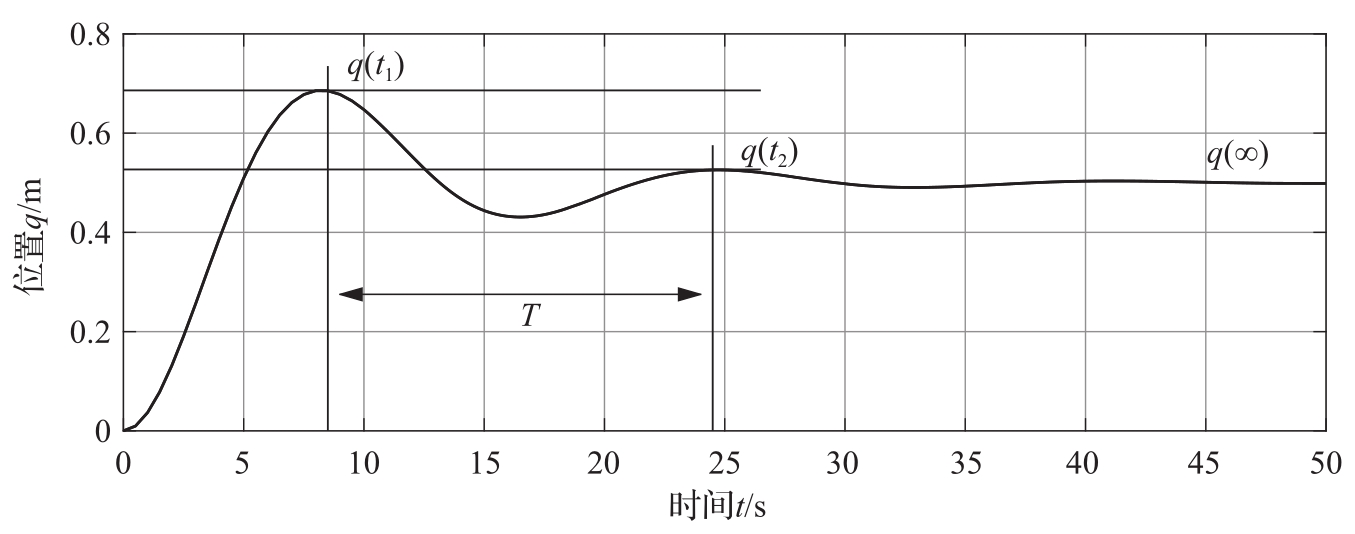
图3.16 弹簧-质量系统的阶跃响应。阶跃输入的幅值是
F
0
=20 N。通过测量响应曲线上相邻的两个局部最大值的时间间隔,可以确定振荡周期
T
。周期、稳态值
q
(∞)以及局部最大值间的相对降幅可以用来估算系统模型的参数

也可以使用许多其他类型的信号来进行实验建模。最常用的是正弦信号(特别是对于具有快速动态的系统),与相关技术相结合,可以测得精确的参数。通过施加不同幅值的输入信号进行重复实验,可以获得非线性程度的指标。对于具有慢动态的系统,基于正弦信号的建模是极其费时的。此时,采用仅在两个不同常数间切换的信号很有优势。有一个很完整的、称作 系统辨识 (system identification)的控制子领域,它专门处理系统模型的实验确定。诸如最优输入、开环和闭环实验、模型精度、基本限制等问题,在其中都得到了广泛的研究。
在推导模型时,引入无量纲的变量往往很有好处。这样处理常常可以降低参数的个数,因而简化系统的方程。这也可以揭示出模型的一些重要特性。通过 标度 (scaling),将变量 归一化 (normalization),可以改进数值计算条件,从而更快、更精确地仿真。
标度的过程在原理上是很直接的:先为每个独立变量选择标度单位,再将每个变量除以选定的标度单位,从而引入新的变量。下面用两个例子来说明这个过程。
再来考虑前面介绍的弹簧-质量系统。忽略阻尼,系统可描述如下:
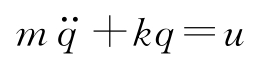
这个模型有
m
和
k
两个参数。为了使模型归一化,引入无量纲的变量
x
=
q
/
l
和
τ
=
ω
0
t
,其中
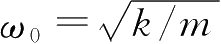 ,
l
是选定的长度标度单位。选取力的标度单位为
mlω
0
2
,引入
v
=
u
/(
mlω
0
2
)。则标度后的方程变为:
,
l
是选定的长度标度单位。选取力的标度单位为
mlω
0
2
,引入
v
=
u
/(
mlω
0
2
)。则标度后的方程变为:
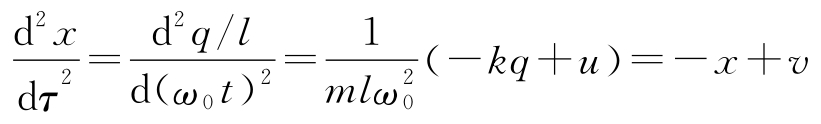
这就是归一化的无阻尼弹簧-质量系统的模型。请注意,归一化的模型没有参数,而原来的模型有
m
和
k
两个参数。在引入经过标度的、无量纲的状态变量
z
1
=
x
=
q
/
l
及
z
2
=
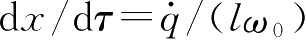 之后,模型可以写成
之后,模型可以写成
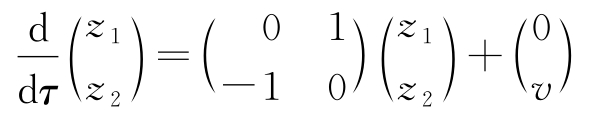
这个简单的线性微分方程描述了任何无阻尼的弹簧-质量系统的动态,跟具体的参数无关,因而让我们可以洞察这种振荡系统的基本动态。为了获得振荡的实际物理频率或幅值,必须对所做的标度进行反向处理。

考虑例3.2中描述的平衡系统。忽略阻尼,故 c =0, γ =0,代入式(3.9),模型可写为:
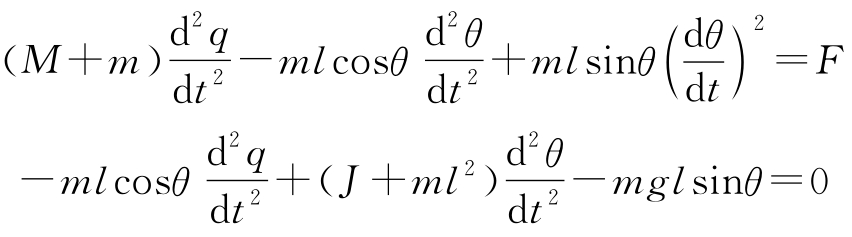
令
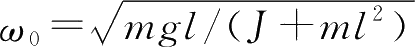 ,取长度的标度单位为
l
,取时间的标度单位为1/
ω
0
,取力的标度单位为(
M
+
m
)
lω
2
,并引入归一化变量
,取长度的标度单位为
l
,取时间的标度单位为1/
ω
0
,取力的标度单位为(
M
+
m
)
lω
2
,并引入归一化变量
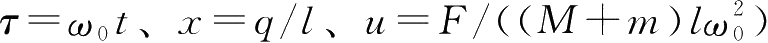 ,则方程变为:
,则方程变为:
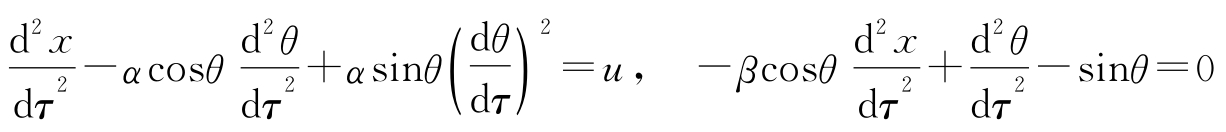
式中, α = m /( M + m ), β = ml 2 /( J + ml 2 )。请注意原来的模型有 m 、 M 、 J 、 l 和 g 这5个参数,但归一化的模型仅有 α 和 β 两个参数。若 M ≫ m 及 ml 2 ≫ J ,那么有 α ≈0和 β ≈1,因此模型可以近似表示为:
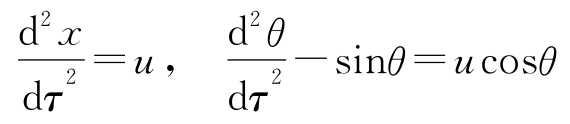
这个模型可以看成是一个质量与一个倒摆的组合,由相同的输入驱动。

对于大型系统来说,标度并不容易,选择很多,但要想选出良好的变量和标度单位,则有赖于对系统的物理特性以及所用的数值分析方法的充分理解。因此,大型系统的标度仍然是一门艺术。