




本节将简要讨论正反馈,尽管它的特性正好与负反馈相反,但在有些场合它还是得到了很好的应用。
具有负反馈的系统可以用线性分析来理解。要了解具有正反馈的系统,则必须考虑非线性效应,因为若没有非线性效应,那么正反馈造成的不稳定性将无限增长。非线性效应可以对信号施加限制,从而产生出有趣又有用的效果。
正反馈可以在许多场合中见到。在生物学中,区分抑制性连接(负反馈)和兴奋性连接(正反馈)已经成为标准做法,如图2.15所示。神经元采用正反馈和负反馈的组合来产生电脉冲。
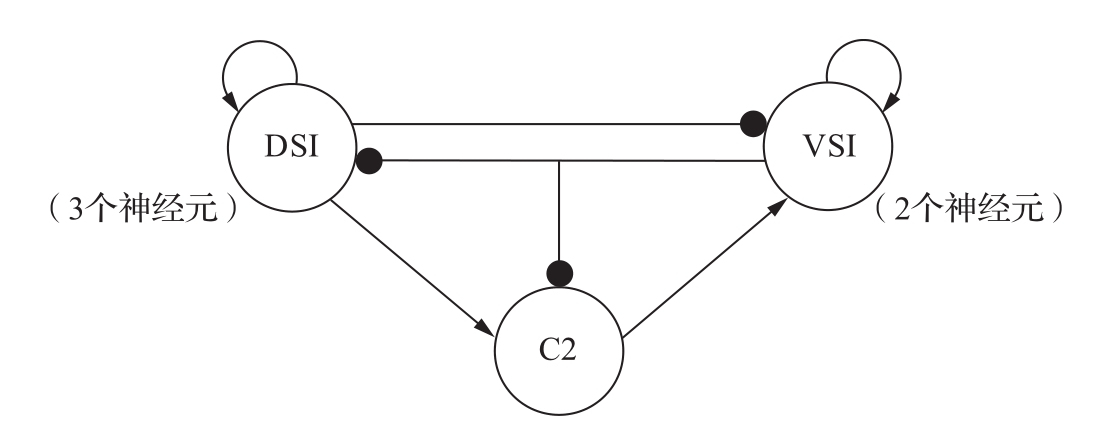
图2.15 海洋软体动物 三岐海兔 (Tritonia)控制游泳运动的神经网络示意图。该神经网络既有正反馈,又有负反馈。兴奋性连接(正反馈)以箭头结尾的连线表示,抑制性连接(负反馈)以圆点结尾的连线表示(图片选编自文献[256])
正反馈可能导致不稳定。指数增长就是一个典型的例子,其中物理量 x 的变化率正比于 x ,即
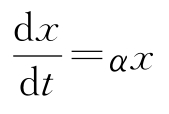
这将导致一个无界的解 x ( t )=e αt 。不过,在自然界中,物种的指数增长会受到食物数量的限制。另一个常见的例子是,在公共广播系统中,当麦克风靠近扬声器放置时,会产生啸声。正反馈可以造成牛群踩踏、银行挤兑,以及繁荣-萧条的周期行为。在所有这些情况下,指数级的增长最终都会受到有限资源的限制。
如2.1节中的例子所示,如果反馈是静态的,那么正反馈和负反馈的定义就是明确的。如果反馈是动态的,那么其作用可能会随着信号频率的变化而从正变负,因此需要特别注意。下面用几个例子来说明正反馈的应用。
1939年,斯坦福大学的威廉·惠利特(William Hewlett)在其硕士论文中巧妙地运用正反馈和负反馈设计了一个稳定的振荡器。该振荡器是惠普公司生产的第一款产品,惠普公司是威廉·惠利特与大卫·普卡德于1939年共同创立的 [200] 。
在20世纪30和40年代,电子电路是以真空管技术为基础的。最简单的真空管放大器有三个电极:阴极、栅极和阳极,一起封闭在玻璃真空管中。阴极用灯丝加热,释放自由电子。在阳极和阴极之间施加很高的正电压,就形成电流。栅极位于阳极和阴极之间,改变栅极上的电压,即可调节电流。电流的大小取决于栅极和阴极之间的电压差,即 V g -V c 。增加此电压差会增大电流。真空管放大器可以看成用栅极电压来控制电流的阀门。
图2.16a所示为惠利特振荡器的原理示意图。该电路中有两个反馈环,信号经两个真空管放大。其中一个环经由
R
1
、
C
1
、
R
2
、
C
2
构成的网络提供从第二管阳极到第一管栅极的正反馈。第二个反馈环经电阻器
R
f
和具有电阻
R
b
的灯泡提供从第二管输出到第一管阴极的负反馈。在适当的增益下,正反馈环产生频率为
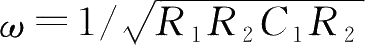 的振荡。该增益由负反馈环确定。由于灯泡的电阻
R
b
会随着温度的升高而增加,因此负反馈环具有非线性增益。
v
out
幅值的增加会导致灯泡的电流增加,从而降低增益。其结果是产生一个幅值和频率稳定的振荡。
的振荡。该增益由负反馈环确定。由于灯泡的电阻
R
b
会随着温度的升高而增加,因此负反馈环具有非线性增益。
v
out
幅值的增加会导致灯泡的电流增加,从而降低增益。其结果是产生一个幅值和频率稳定的振荡。
在图2.16b所示使用运算放大器的等效实现中,反馈环更为清楚。
早期的反馈控制器通过将一阶动态系统连接成正反馈来实现积分作用,如图2.17的框图所示。比例反馈通常会产生稳态误差。这个问题可以通过添加偏置信号抵消稳态误差来解决。在图2.17中,对控制信号进行低通滤波,再将滤波后的信号加回到控制信号的路径上。这有助于补偿存在的任何误差。
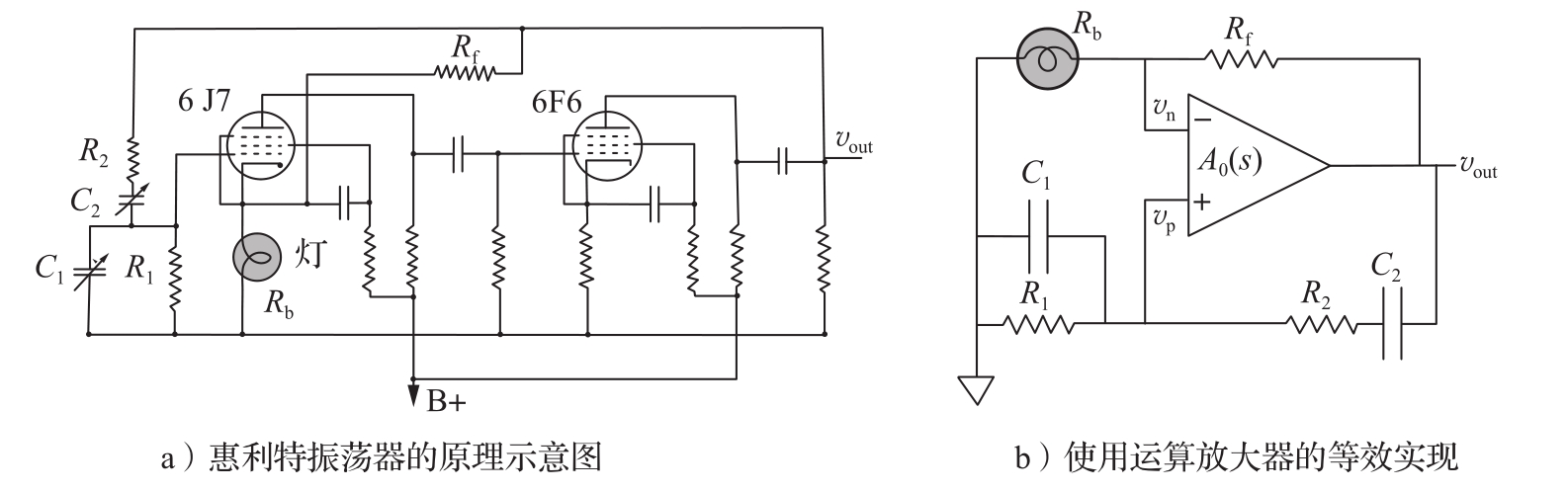
图2.16 威廉·惠利特的振荡器电路图
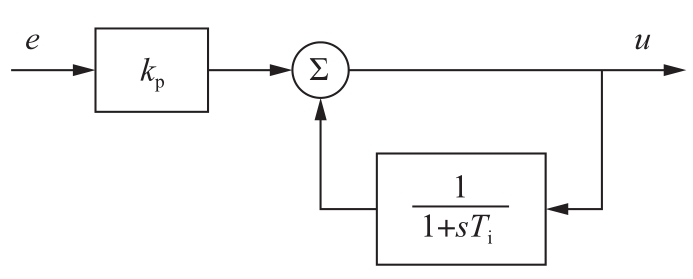
图2.17 用正反馈实现积分作用
稍加分析可以更好地理解该电路。利用框图代数运算可以得到系统的传递函数为:
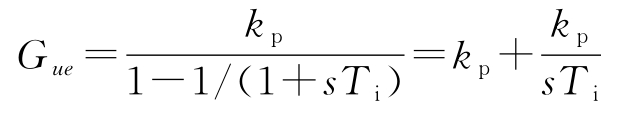
这是PI控制器的传递函数。如今,这种实现积分作用的方法仍被许多工业调节器所采用。
将线性和非线性的元件与正反馈相结合,可以使系统获得一些有趣又有用的性质。这里介绍一个使用反馈电路实现简单形式的存储器的例子。
考虑图2.18所示的系统,它由一个具有一阶动态的线性块和一个具有正反馈的非线性块组成。假设非线性块可描述为:
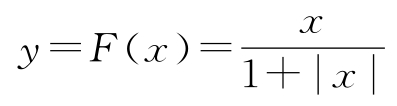
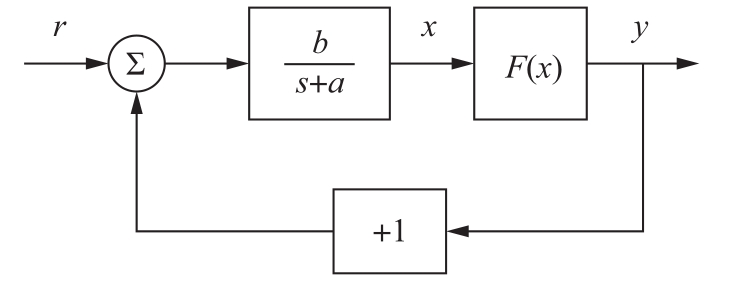
图2.18 具有正反馈和饱和特性的系统的框图。参数为 a =1、 b =4
由此得:
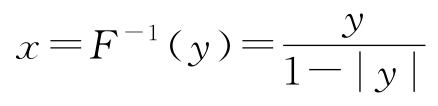
描述系统的微分方程为:
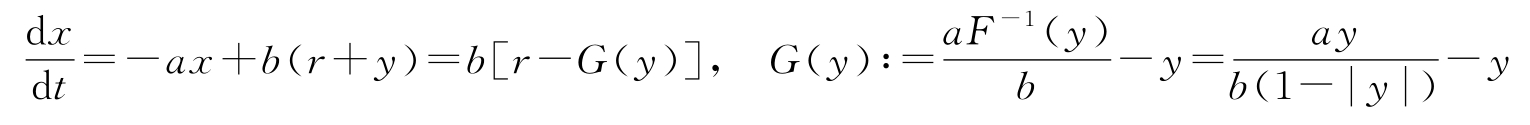
用变量 y = F ( x )重写动态方程,可以得到输入 r 和输出 y 之间的以下关系:
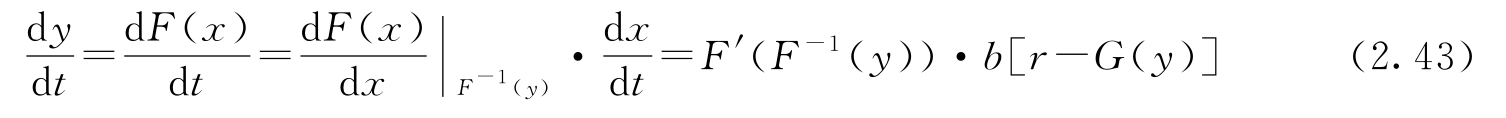
对于所有
x
,
F′
(
x
)>0,故函数
F
是单调的,因此,对于恒定输入
r
,平衡点由
r
=
G
(
y
)的解确定。
a
=1、
b
=4时,函数
G
(
y
)的曲线如图2.19a所示。函数
G
(
y
)在
y
=-1+
 处有局部最大值
处有局部最大值
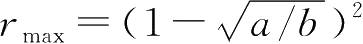 =0.25,在
y
=0.5处有局部最小值
r
min
=-0.25。系统可能的平衡点集可以在图2.19a中通过固定
r
并识别满足
r
=
G
(
y
)的所有
y
值来确定。当
=0.25,在
y
=0.5处有局部最小值
r
min
=-0.25。系统可能的平衡点集可以在图2.19a中通过固定
r
并识别满足
r
=
G
(
y
)的所有
y
值来确定。当
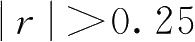 时,有唯一的平衡点;当
时,有唯一的平衡点;当
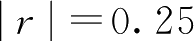 时,有两个平衡点;当
时,有两个平衡点;当
 时,有三个平衡点。
时,有三个平衡点。
微分方程(2.43)是一阶的,如果
G′
(
y
e
)为正,则平衡点
y
e
是稳定的,如果
G′
(
y
e
)为负,则不稳定。在图2.19a中,稳定平衡点以实线标出,不稳定平衡点以虚线标出。可见,当
r
min
<
r
<
r
max
时,微分方程有两个稳定平衡点,当
 时,有一个稳定平衡点。
时,有一个稳定平衡点。
为了解系统的行为,研究当参考信号改变时会发生什么。如果参考 r 为零,则有两个稳定平衡点,这可以在图2.19a中通过 r =0的水平线(标记为C)看出。假设系统处于左侧的稳定平衡点,此处 y 为负值。如果增大参考 r ,平衡点将稍微右移。当参考 r 达到0.25时(该值对应不稳定平衡点),则解会移动到右侧的稳定平衡点,此处 y 为正值,如图2.19a中标记为B的线所示。如果参考 r 进一步增大,输出 y 也会增大。因此,静态输入/输出关系由“反函数” y = G † ( r )给定,它以 r 表示的函数形式给出了稳定输出值。该系统具有如图2.19b所示的滞环输入/输出关系,图中的虚线标明了解的分支之间的切换点,这发生在 r =± r max =±0.25处。
系统的时域行为如图2.19c的仿真结果所示,其中虚线为输入 r ,实线为输出 y 。信号的波形取决于参数:图中选取了 a =5、 b =50,以便看到更明显的分支切换。滞环宽度为2 r max ,参数 a 确定了输出转角处的尖锐程度。图2.18所示的电路常被用作检测信号变化的触发器(称施密特触发器)。它也被用作固态存储中的存储元件,这表明反馈可用于产生离散行为。
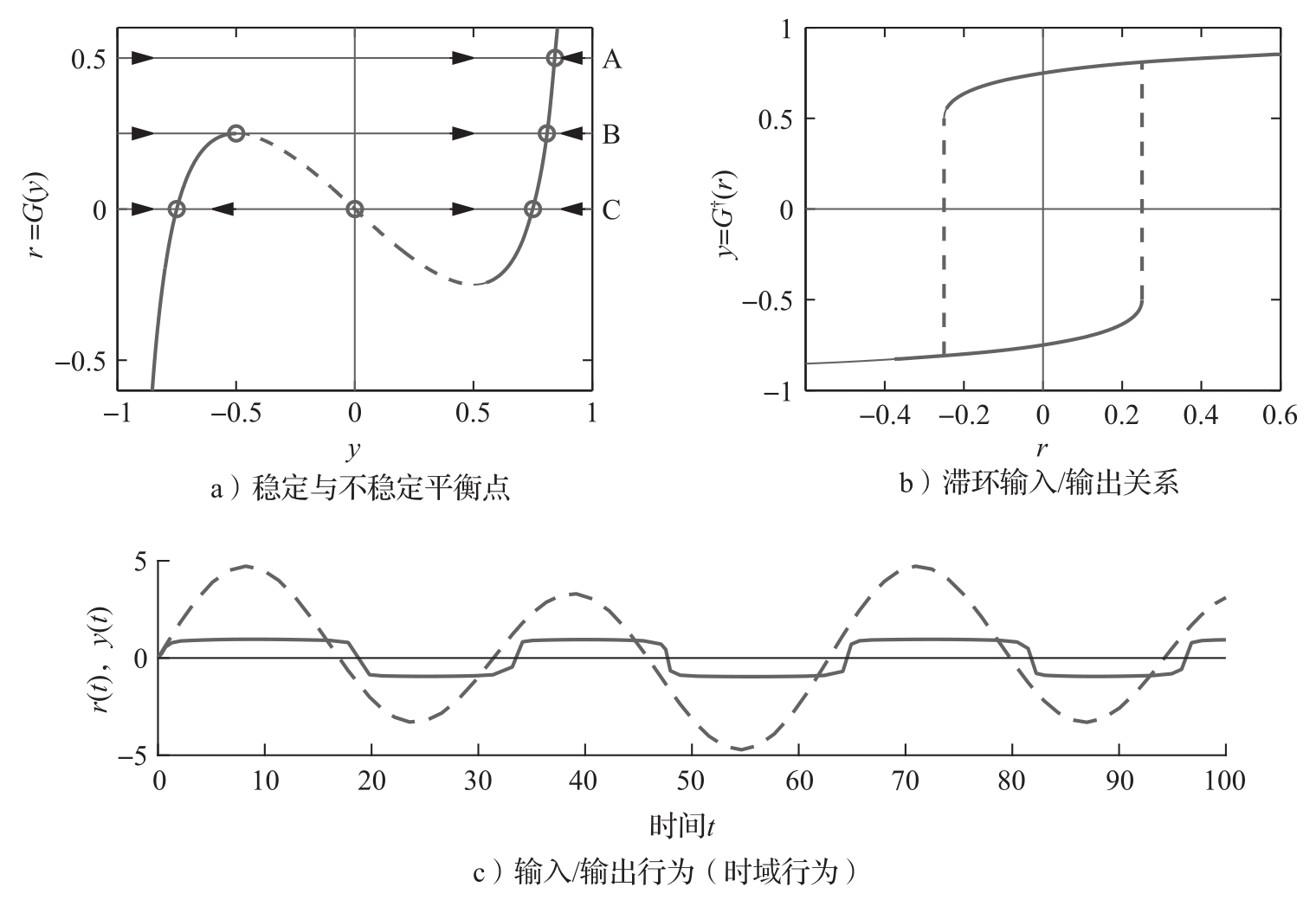
图2.19 具有正反馈和饱和特性的系统。图a中,对于一个固定的参考值 r ,它与曲线 r = G ( y )的交点对应系统的平衡点。在选定的几个 r 值处,用圆圈标出了它们的平衡点(请注意,对于某些参考值,有多个平衡点)。箭头对应导数 G ′( y )的符号,表示 y 离开平衡点(-)或靠近平衡点(+)。 r = G ( y )的实线部分代表稳定平衡点,虚线部分代表不稳定平衡点。图b为由 y = G † ( r )给出的滞环输入/输出关系图,可见,某些 r 值具有单一平衡点,另外一些值则有两个可能的(稳定)稳态输出值。图c为系统动态的仿真结果,虚线为参考 r 的曲线,实线为输出 y 的曲线