




首先介绍用静态模型表示过程和控制器的行为特性的方法。虽然这类模型非常简单,却非常有助于深刻理解反馈的基本特性。负反馈的基本特性是能增大线性范围,改进对参考信号的跟踪,降低干扰、参数变化等的增益与影响。适度的正反馈则具有相反的特性:会缩小线性范围,增大系统的增益。在临界值下,增益将变成无穷大,系统的行为将类似于继电器;较大的增益会导致滞环行为。尽管静态模型能为读者提供一些参考,但它们无法捕捉动态现象(稳定性等)。正反馈与动态特性相结合,往往引起不稳定和振荡,这将是本书从头至尾一直要讨论的问题。
考虑图2.1所示框图中的闭环系统,图中参考(或命令)信号为 r ,即期望的系统输出。控制器 C 的输入为 e ,它等于参考 r 和过程输出 y 之间的差值,控制器的输出是控制信号 u 。在过程的输入中还存在负载干扰 v ,它使系统受到干扰。虽然本书重点研究负反馈,但图2.1也可以用于分析正反馈。
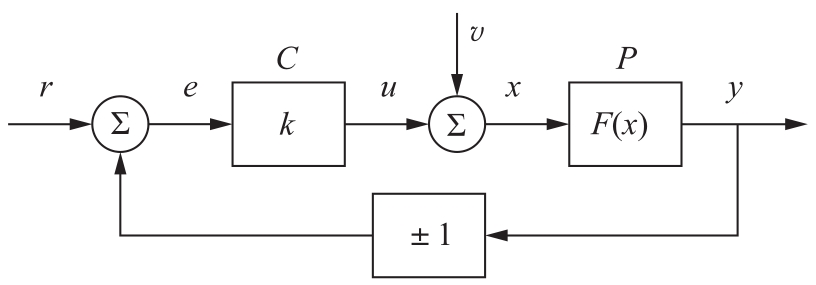
图2.1 简单的静态反馈系统框图。控制器恒定增益 k >0,过程用非线性函数 F ( x )建模。过程输出为 y ,控制信号为 u ,外部信号为参考 r ,负载干扰为 v 。底部方块中的“+”“-”符号分别表示正反馈和负反馈
将过程 P 建模为这样一个函数:当输入的幅值小于1时,函数是线性的;当输入的幅值大于1时,函数具有饱和特性。控制器则建模为恒定的增益 k 。由此,过程和控制器表示为以下函数:
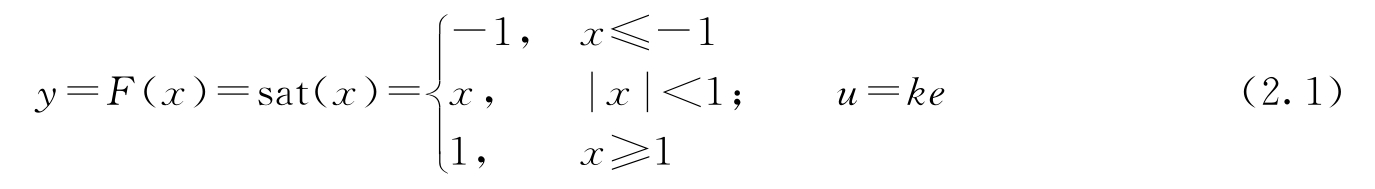
当
 时,
y
=
x
,
过程增益
(process gain)为1,且过程是线性的,这个范围称作
线性范围
(linear range)。由于控制器的输出
u
是输入
e
的
k
倍,因此
控制器增益
(controller gain)为
k
。
时,
y
=
x
,
过程增益
(process gain)为1,且过程是线性的,这个范围称作
线性范围
(linear range)。由于控制器的输出
u
是输入
e
的
k
倍,因此
控制器增益
(controller gain)为
k
。
当没有反馈时,控制器和过程组成的系统称为 开环系统 (open loop system)。当忽略干扰 v 时,由式(2.1)可以得到开环系统的输入/输出关系,即

它具有增益
k
和线性范围
 。
。
为了研究过程输出 y 对参考信号 r 的跟踪,假定图2.1中的负载干扰 v 为零。先考虑 负反馈 (negative feedback)的情况,将图2.1中下部方块中的符号设置为-1。根据图2.1及式(2.1),可得闭环系统的描述为:

消除式中的 u ,可得:

为了找到参考信号
r
和过程输出
y
之间的关系,需要求解代数方程。在线性范围
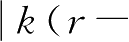
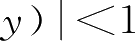 内,有
内,有
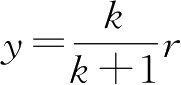 。当
。当
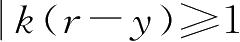 时,输出饱和,有
y
=±1[具体取决于
k
(
r-y
)的符号]。可以证明,完整的输入/输出关系满足:
时,输出饱和,有
y
=±1[具体取决于
k
(
r-y
)的符号]。可以证明,完整的输入/输出关系满足:
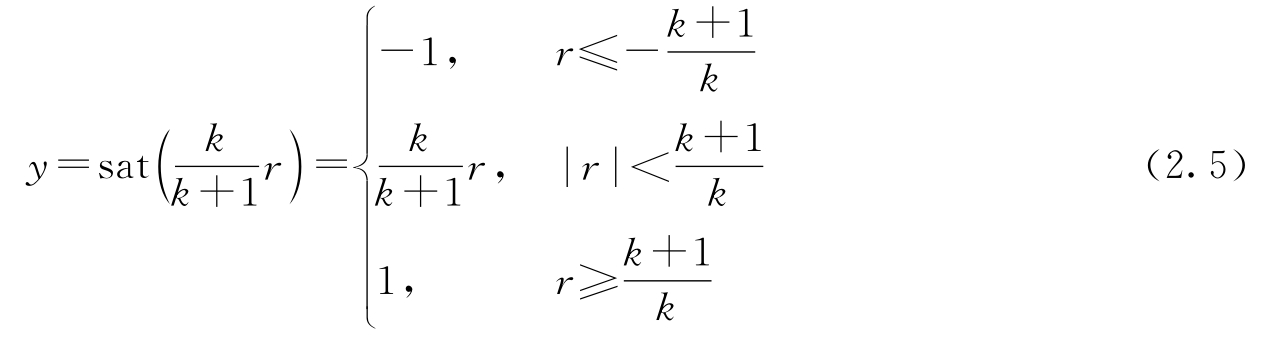
函数图像如图2.2所示。
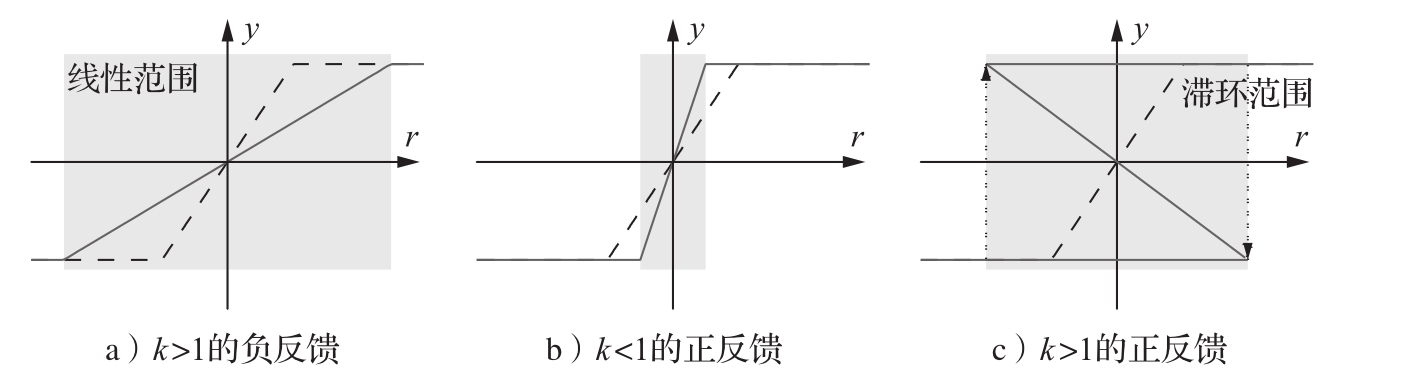
图2.2 系统的输入/输出行为。图a为 k >1的负反馈情况;图b为 k <1的正反馈情况;图c为 k >1的正反馈情况。实线为闭环系统的响应,虚线为开环系统的响应(重绘自文献[221]的图20.5)
该闭环系统的线性范围为
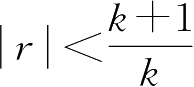 。对比式(2.2)可见,负反馈把系统的线性范围扩大为开环系统的
k
+1倍,具体如图2.2a所示(虚线为开环系统的,实线为闭环系统的)。
。对比式(2.2)可见,负反馈把系统的线性范围扩大为开环系统的
k
+1倍,具体如图2.2a所示(虚线为开环系统的,实线为闭环系统的)。
接下来研究闭环系统对增益变化的灵敏度。系统的 灵敏度 (sensitivity)描述系统性能受系统参数变化影响的程度。对于工作在线性范围内的开环系统,因 y = kr ,故有:

可见,输出的相对变化等于参数的相对变化,灵敏度为1。所以,在开环系统中, k 变化10%将导致输出变化10%。
对于输入处于线性范围内的闭环系统,根据式(2.5)有:
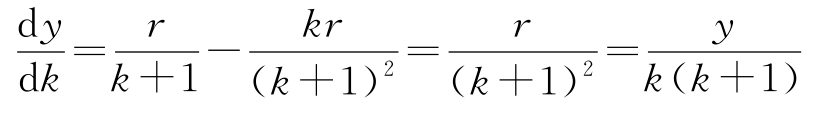
因此,

对比式(2.6)可见,增益为 k 的负反馈会将系统对增益变化的灵敏度降低为开环时的1/( k +1)倍。例如,如果 k 为100,则 k 变化10%引起的 y 的相对变化将小于0.1%。因此闭环系统对参数变化的灵敏度要低得多。
以上的分析也可用于研究正反馈的影响。如果将图2.1中反馈环的-1代替为+1,则式(2.5)变成:

请注意,当
k
<1时,该闭环系统的增益为正数,且比开环增益大,如图2.2b所示。其线性范围为
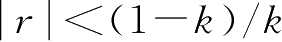 。对比式(2.2)的开环系统可见,
k
<1的正反馈将线性范围缩小为开环的1
-k
倍。当
k
趋近于1时,闭环增益趋向于无穷大,线性范围缩小到零,系统的行为类似于继电器。
。对比式(2.2)的开环系统可见,
k
<1的正反馈将线性范围缩小为开环的1
-k
倍。当
k
趋近于1时,闭环增益趋向于无穷大,线性范围缩小到零,系统的行为类似于继电器。
对于
k
>1的正反馈,由式(2.8)可知闭环增益为负,如图2.2c所示,且当
k
趋向于无穷大时,增益趋向于-1。当正反馈的增益较大时,对于
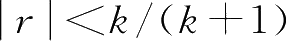 范围内的输入,其输入/输出特性具有多个输出值的特点,闭环系统的行为类似于一个具有滞环特性的开关。在2.6节中,我们将更深入地探讨这一概念,可以看到,如果考虑过程的动态,那么输入/输出特性曲线上具有负斜率的所有点都是不稳定的。
范围内的输入,其输入/输出特性具有多个输出值的特点,闭环系统的行为类似于一个具有滞环特性的开关。在2.6节中,我们将更深入地探讨这一概念,可以看到,如果考虑过程的动态,那么输入/输出特性曲线上具有负斜率的所有点都是不稳定的。
本书的重点是研究负反馈,但有些系统利用了正反馈,以下就是一个这样的例子。
当埃德温·阿姆斯特朗(Edwin Armstrong)还是哥伦比亚大学的一名本科生的时候,他于1914年制造了一个只用一个真空管的“ 超再生 ”(superregenerative)无线电接收器。超再生无线电接收器(放大器)可以建模为一个开环增益为 k 且具有饱和输出特性的放大器与正反馈相结合的系统,如图2.1所示。利用式(2.8),可以算得闭环系统的增益为 k cl = k /(1 -k )。选择反馈增益 k 略低于1,可以获得非常大的闭环增益。例如,选择 k =0.999,可得 k cl =999,这是一个增加了近三个数量级的增益。
使用正反馈的缺点是系统高度灵敏,必须仔细调整增益以避免振荡。例如,如果增益 k 是0.99而不是上面的0.999(差别小于1%),那么闭环增益将变为 k cl =99,差了10倍(或1000%)。该电路的振荡特性使得分析放大器必须使用更为高级的(动态的)模型。
尽管存在局限性,但这种放大器在简单的对讲机、车库开门器和玩具中仍在使用。

反馈的另一个用途是减少外部干扰(图2.1中的负载干扰 v )的影响。对于开环系统, v ≠0时的输出为
y =sat( kr + v )
因此,在线性范围内, v 和 y 之间的增益为1,即干扰通过时没有衰减。
为了研究反馈对负载干扰的影响,考虑图2.1中具有负反馈的系统。为简单起见,将参考信号 r 设置为零。负载干扰 v 与输出 y 之间的关系为 y =sat( v-ky ),它是一个代数方程。在线性范围内,可得 y = v /( k +1),更一般地,可以证明:

因此,在线性范围内,负反馈使负载干扰的影响降低到原来的1/( k +1)倍。
综合以上三种情况的分析可见,负反馈增大了系统的线性范围,降低了系统对参数不确定性的灵敏度,并减轻了负载干扰的影响。付出的代价是降低了闭环增益。正反馈正好相反:它使闭环增益增大,但付出的代价是增大了灵敏度,放大了干扰的影响。