




完全根据电器位置分布,以物理链接和线束最短的原则构建网络。针对一种理想的全分布式系统,并且对网络层级而言,仅包括骨干网、局域网及电源网,电控单元通过上述三个网络连接,其结构如图3-1所示。
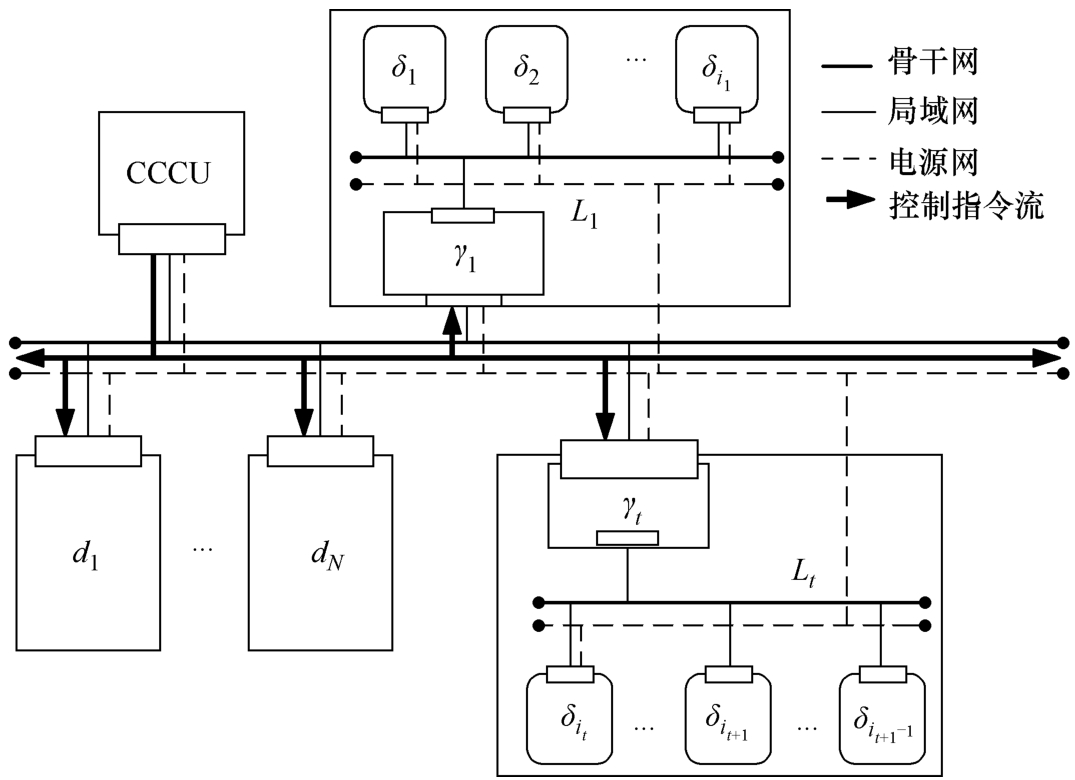
图3-1 分布式汽车电子电气架构与组网
如图3-1所示,每个局域网 L t ,包含一组ECU和一个网关 γ t 。
中央计算单元(Central Computational Unit,CCU)用于执行整车车身电器系统的控制逻辑,协调整车电器正常工作。由于CCU的存在,每个ECU只保留其与所控执行器或传感器最基本功能,这样大大降低了单个智能节点的计算需求,并且能与其他电器实现逻辑和控制上的独立。
与骨干网直接相连的称为骨干ECU(图中 d i ),骨干ECU通常为与安全相关较大的ECU或与网络交换信息较多或时效性要求比较高的ECU。其余的ECU均被列为局域ECU(如图3-1中的 δ i )。
汽车线束的布置受到机械结构的约束,一般情况下骨干线束通过汽车车身的走线槽、走线孔、定位卡等结构,可以贯穿整个车身。典型的汽车骨干线束布置如客车电U形和L形布置;乘用车经常使用的H形和E形布置。
将骨干线束由头到尾“拉直”作为 X 轴,并在一端定义0点,干线上的分支 Y i , i =1,2,…,保持与干线垂直。在根据骨干线束定义的直角坐标系中,由于车身电器通过电器分支与骨干线束相连,因此车身电器的空间位置可以由其中骨干线束上的投影点点替代,如图3-2所示。
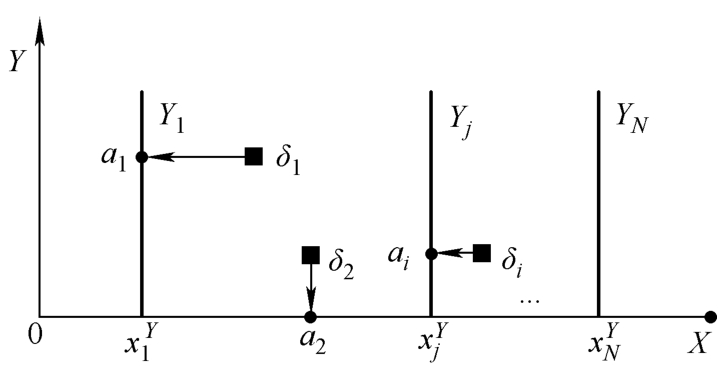
图3-2 骨干线束坐标系及电器位置坐标
在图3-2中, δ 1 、 δ 2 、 δ i 的空间位置坐标分别可由分支点 a 1 、 a 2 、 a i 在骨干线束坐标系中的坐标( x 1 , y 1 ),( x 2 , y 2 ),( x i , y i )来表示。
采用骨干线束干线上的投影点(如图3-2的 a 2 )替代还是支线上投影点(如图3-2中的 a 1 )替代,取决于ECU(点)到骨干线束(干线和支线)的距离,应以最小距离的投影点进行替代。
如果将ECU按位置坐标大小进行排列,先按 x 坐标从小到大排列,当 x 坐标相等的时候按 y 坐标由小到大排列,得到电器按坐标排列的有序列为

对于上式中的任意 δ i , δ j ∈ Δ 有

ECU δ i 与 δ j 之间的线束距离定义为
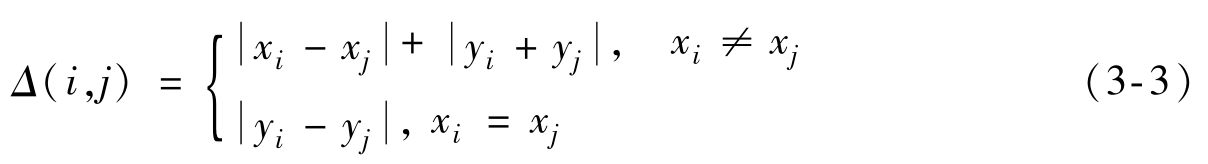
式中,( x i , y i ),( x j , y j )分别为电器在骨干线束总线坐标系中的坐标。线束距离具有明确的物理意义,即在可布线空间的约束条件下,从电器 δ i 到 δ j 需要的不变线束长度。
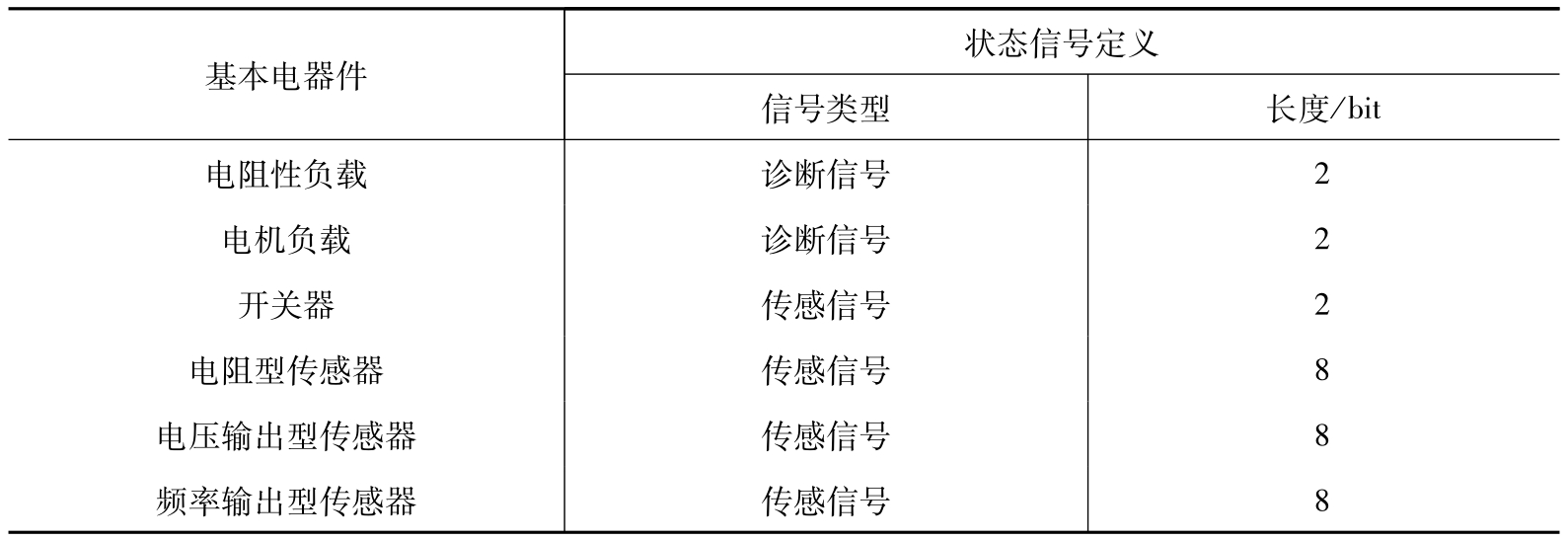
对任一子网 L t ,网络中传输的信号包括用于对ECU进行控制的控制指令信号和电器输出的状态信号。由全分布式系统结构可知,对任意一个子网,其中的控制指令帧都相同。状态信号包括传感信号和故障信号等,是由电器发给网关,再转发到骨干网上。不同类型的ECU具有不同的信号定义和不同的信息量,因此状态信号所占用的长度也不相同。以典型的车身电子控制系统为例,对控制信号的传输需求见表3-1。
表3-1 车身电器的信号传输需求
一般来说,传感器信号都是周期型信号,故障信号可以是事件型的信号,为方便设计起见,可以将它们都设置成周期型。周期型信号的发送周期则需要根据具体电器对实效性的要求不同而定义,一般车身电器系统中,信号的传输周期为100~1000ms。
对于所有的ECU,其控制指令都根据汽车总线(这里以LIN总线为例)的特点在应用层编码,然后打包在若干帧里面,对于电器输出的状态信号,则至少需要一帧,而在LIN规范中,又要求其长度为偶数,因此ECU状态信号最后成帧的数据部分长度 N i 为

式中, l i 为电器 δ i 的信号长(bit); N i 为电器 δ i 的信号帧长度(Byte)。
LIN消息在总线上的传播时间由三部分构成:帧头、响应间隔和响应,因此消息的传播时间为
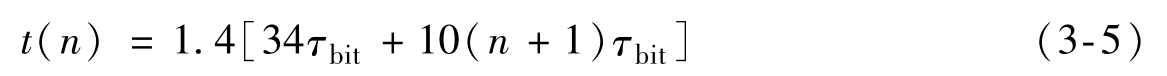
式中, τ bit 是在给定波特率下每一位传输所需时间; n 是消息长度。在不同技术的网络和不同的波特率下,消息传输的延时不同,根据具体情况来计算。
通过对ECU进行排序,将子网组网的问题转化为 n 个ECU划分成 k 个类的问题,即有序样品的聚类分析问题。
对于第 t 个类 G t , t =1,2,…, m ,定义其直径 D t 为

式中, d ( i t , i t +1 -1)为ECU间距离,其长度由公式(3-4)定义,定义分类的损失函数为

这里的直径 D t 实际上就是子网 G t 所需的线束长度,损失函数为所有子网线束总长度。对ECU的组网问题,就转化为求解一种分割方法 b ( n , m ),使得损失函数 L 最小。
根据上述,子网组网的优化模型可描述为
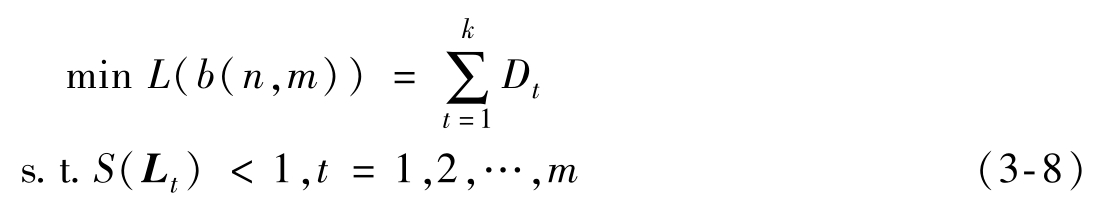
由于式(3-8)所描述的优化模型带有约束条件,表明对该有序ECU序列进行分割时,类内部元素的个数及其某属性总和不能超过一定容量,因此无法采用一般的聚类方法。考虑到解的离散性及问题的规模,采用全局搜索方法,根据LIN协议的规定,LIN网络的控制器数量一般不能超过16个,而少于4个ECU组成的网络则没有意义,记 i t 为第 t 组最后一个ECU编号,总分组数(即网络数)为 m ,则根据网络内ECU数量的限制,可在多维整数空间 B 中进行搜索:
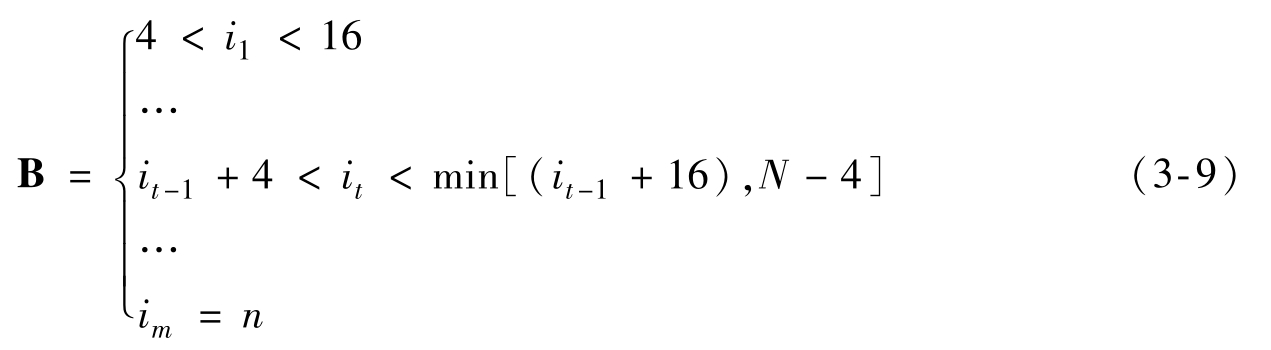
式中, n 为ECU数量。在网络负载“平均”分配的理想情况下,网络数 m 可由下式求得
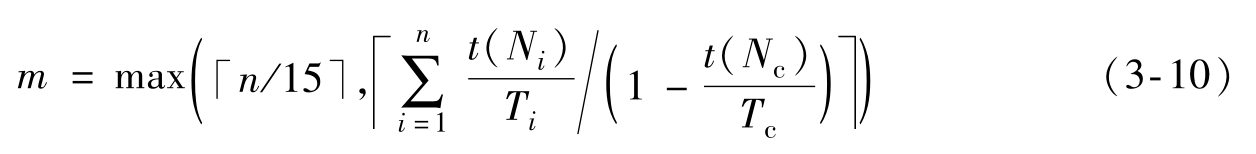
事实上,由于网络负载分配并不按有序样品序列均匀分配,因此最终可行的网络数 m 比式(3-10)计算的要多。由于每个分割点最多搜索12次,网络数15< m < n /4,该算法的时间复杂度 T ( n )为

汽车内部ECU数量总是十分有限的,因此搜索范围并不是很大,因此利用该算法进行数值求解完全可行。最终其算法流程如图3-3所示。
由图可知,算法的步骤为:
1)算法启动,根据式(3-10),计算初始网络数量。
2)遍历搜索空间 B ,针对每个分法判断网络可调度条件并求解损失函数 L ( b ( n , m )),这里初始损失函数可取 d (1, n )。
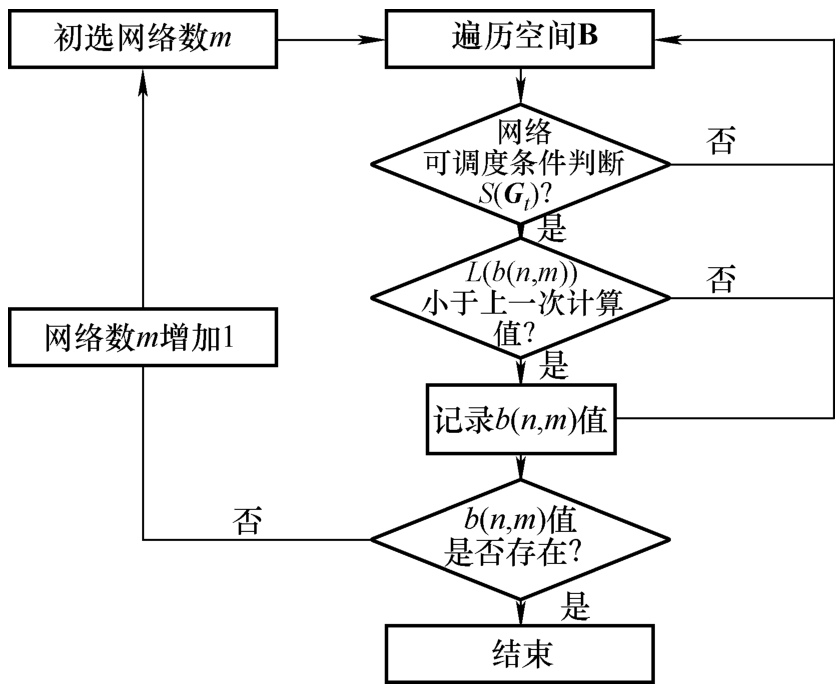
图3-3 有序样品的有限容量最优聚类求解计算流程
3)如果记录值 b ( n , m )存在,则该值为最优解。
4)如果记录为空,则令 m = m +1,重复第2)和第3)步过程,直到求得满足条件的解。
通过组网优化模型构造、并考虑网络通信的可调度约束条件,然后利用有序样品的聚类分析法就能得到分布式架构中网络组织的优化方法。当然在实际的情况中不可能如图3-1所述那么完美,ECU与车载电器(执行器/传感器等)总是混合存在,并非所有的执行器和传感器都能够自带控制单元。