




从研究轮胎振动的角度,我们只关心路面激励对轮心的传递,即胎面激励是输入,轮心振动是响应。如果研究轮胎单体(自由轮胎),也可以在轮心处施加力输入,而胎面响应为输出。
为了研究轮胎传递函数、传递率、模态等动态特征,需要了解四种典型的传递函数。图3.1给出了传递函数的激励点和响应点。
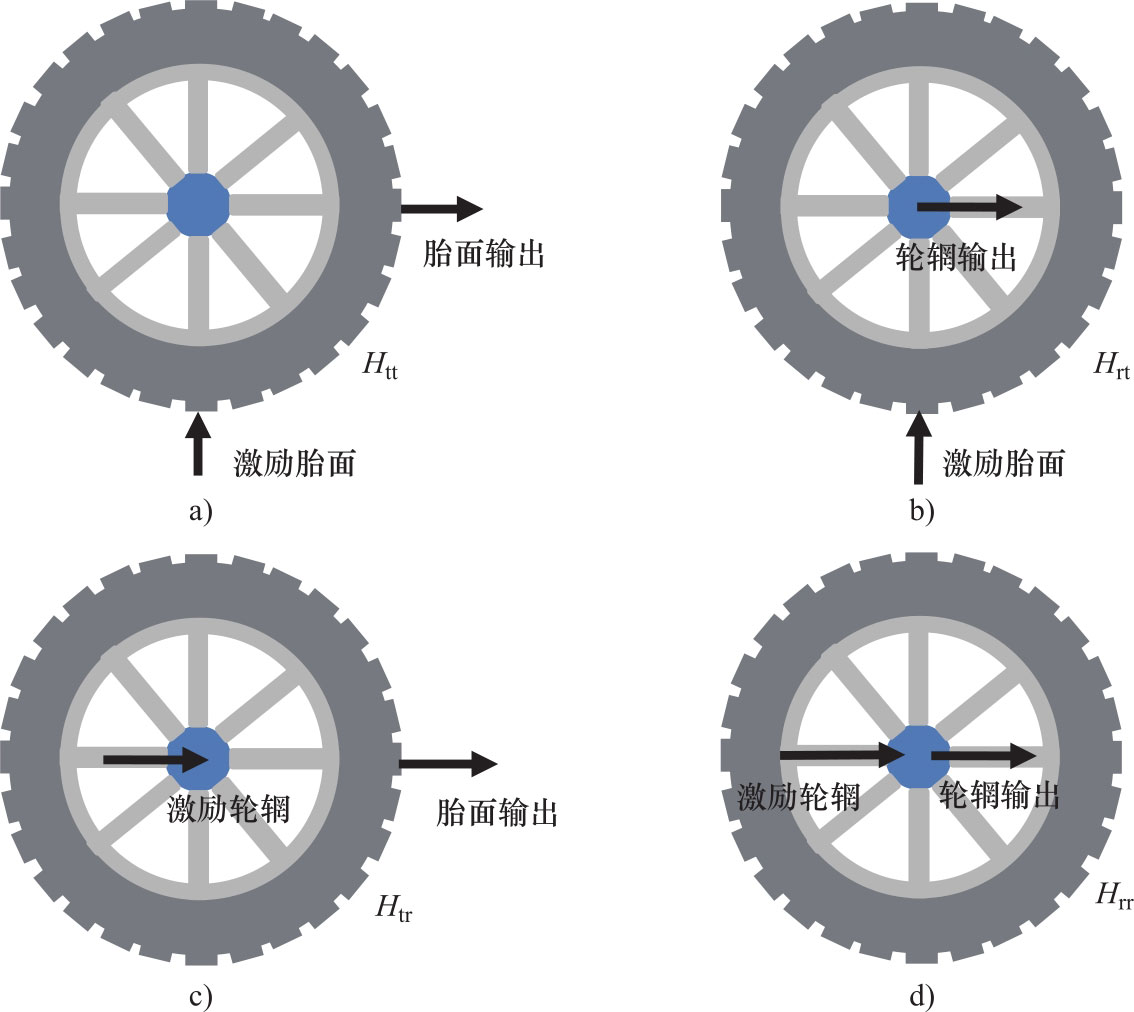
图3.1 轮胎四种传递函数的激励点和响应点
1)激励胎面,胎面响应:胎面对胎面的传递函数 H tt ,称为胎面-胎面传递函数。
2)激励胎面,轮辋响应:轮辋对胎面的传递函数 H rt ,称为轮辋-胎面传递函数。
3)激励轮辋,胎面响应:胎面对轮辋的传递函数 H tr ,称为胎面-轮辋传递函数。
4)激励轮辋,轮辋响应:轮辋对轮辋的传递函数 H rr ,称为轮辋-轮辋传递函数。
分析轮胎传递函数的目的有以下4个方面:
第一,了解轮胎的动态特征,如线性与非线性特征。通过激励胎面,得到轮辋响应,以及激励轮辋,得到胎面响应,来比较互逆性是否成立。
第二,为模态分析提供数据。传递函数是模态分析的基础,即只有得到了系统上一系列点的传递函数,才能得到模态振型。
第三,为传递率计算提供基础。本章第六节将介绍轮胎传递率的定义、测试和计算方法。传递率是以传递函数为基础来计算的。
第四,了解轮胎响应与激励的关系,即激励不同位置,其他位置的频率响应特征。比如激励胎面,来了解胎面响应与轮辋响应的差异。
轮胎传递函数可以通过模型(如有限元模型)和试验获取,而试验数据更能真实地反映轮胎特征。本章第三节将在轮胎模态试验部分介绍传递函数的测试方法。下面就以测试结果来分析轮胎传递函数的特征。
研究轮胎互逆性的目的是了解胎面响应对轮辋激励传递函数与轮辋响应对胎面激励传递函数之间的关系,即确定这两个传递函数是否互逆。测量时,轮胎处于自由边界状态,用激振器和力锤来施加力。当施加力超出一定值时,轮胎会移动。在确保轮胎不移动情况下,使用最大激励力。
图3.2是一个轮胎(215/50R17)的两条垂向传递函数测试曲线。一条是轮辋响应对胎面激励的传递函数( H rt ),一条是胎面响应对轮辋激励的传递函数( H tr )。在300Hz之内,这两条曲线基本重合,即这个轮胎传递函数满足互逆性原则,所以可以认为轮胎是一个线性结构。这两条曲线上有三个明显的峰值。第一个和第二个峰值对应的频率分别是86Hz和97Hz,为轮胎结构模态频率。第三个峰值对应的频率是221Hz,为轮胎声腔模态频率。
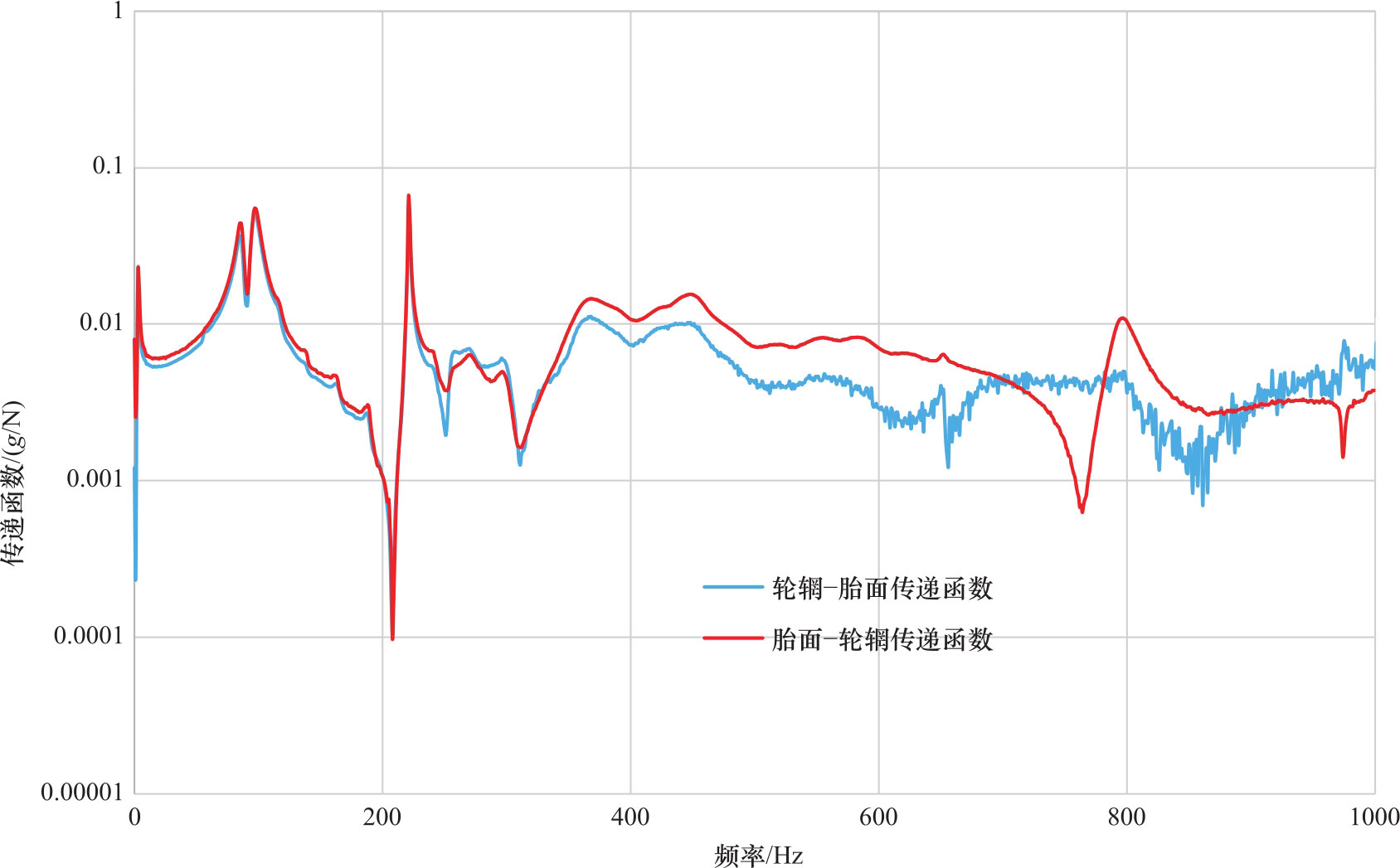
图3.2 某个轮胎的轮辋-胎面和胎面-轮辋传递函数测试曲线
为了进一步证明轮胎线性特征,表3.1给出了另外四个轮胎的传递函数测试曲线。它们的特征与图3.2相同,即它们都满足互逆性原则,都有两个轮胎结构模态频率峰值和一个声腔模态频率峰值。
表3.1 四个轮胎的轮辋-胎面和胎面-轮辋传递函数测试曲线
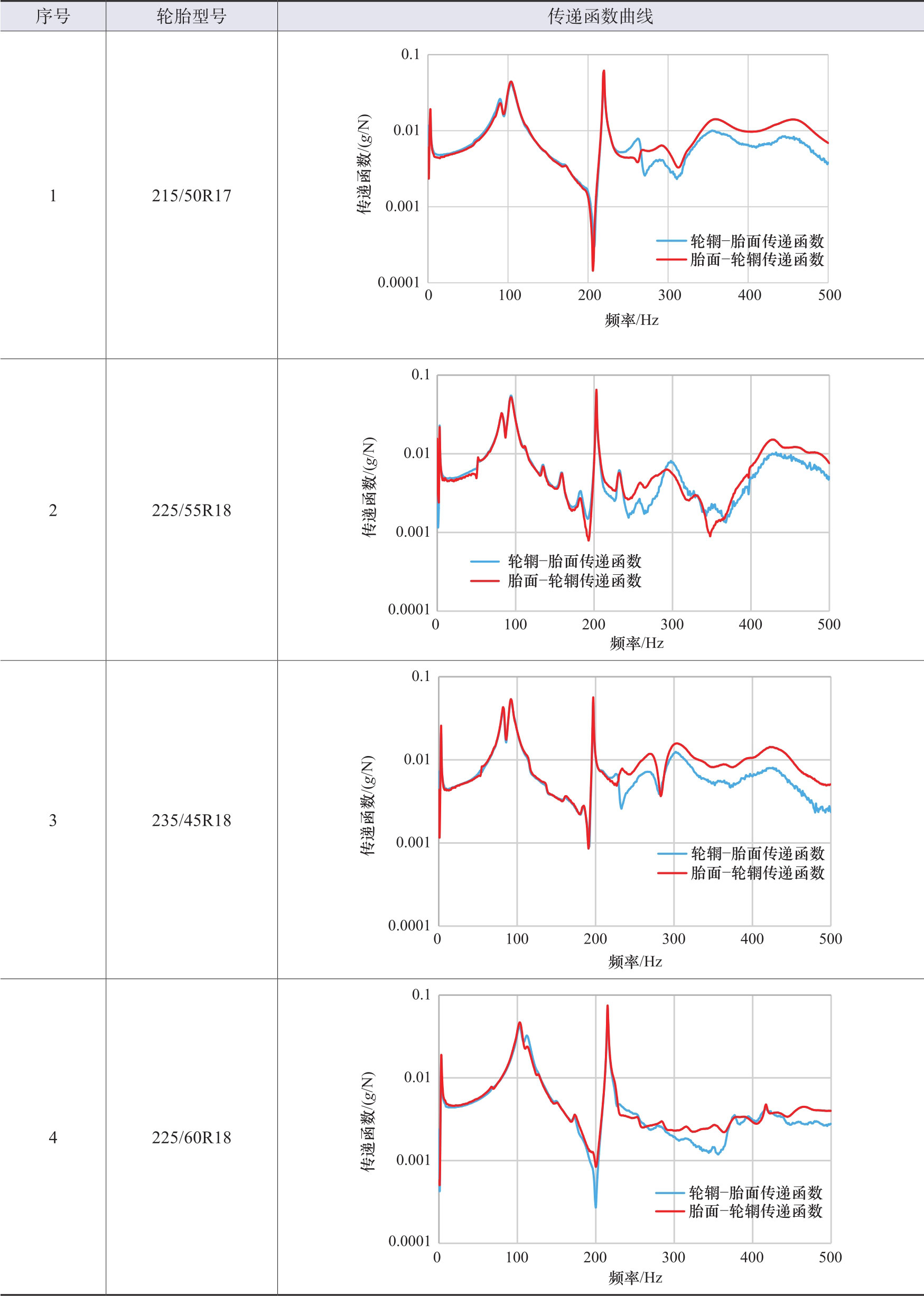
图3.3是一个轮胎(215/50R17)的垂向胎面-胎面传递函数( H tt )和轮辋-轮辋传递函数( H rr )测试曲线。这两种传递函数曲线有比较大的差别。胎面-胎面传递函数在80~250Hz频率范围内有密集峰值,它们对应着胎的径向模态,代表了胎的弹性结构特征。轮辋-轮辋传递函数在低频86Hz和99Hz处有两个峰值,对应着轮辋模态。大多数轮辋材料是铝合金,其单体固有频率大于300Hz,因此这两个轮辋模态是轮辋与胎的轮胎横向弹性模态。在轮辋-轮辋传递函数上有221Hz的峰值,而在胎面-胎面传递函数上也有个小峰值,对应着声腔模态,这说明声腔模态对轮辋的传递大于对胎面的传递。因此,敲击胎面得到轮胎径向模态,而敲击轮辋得到轮胎横向模态与空腔模态。
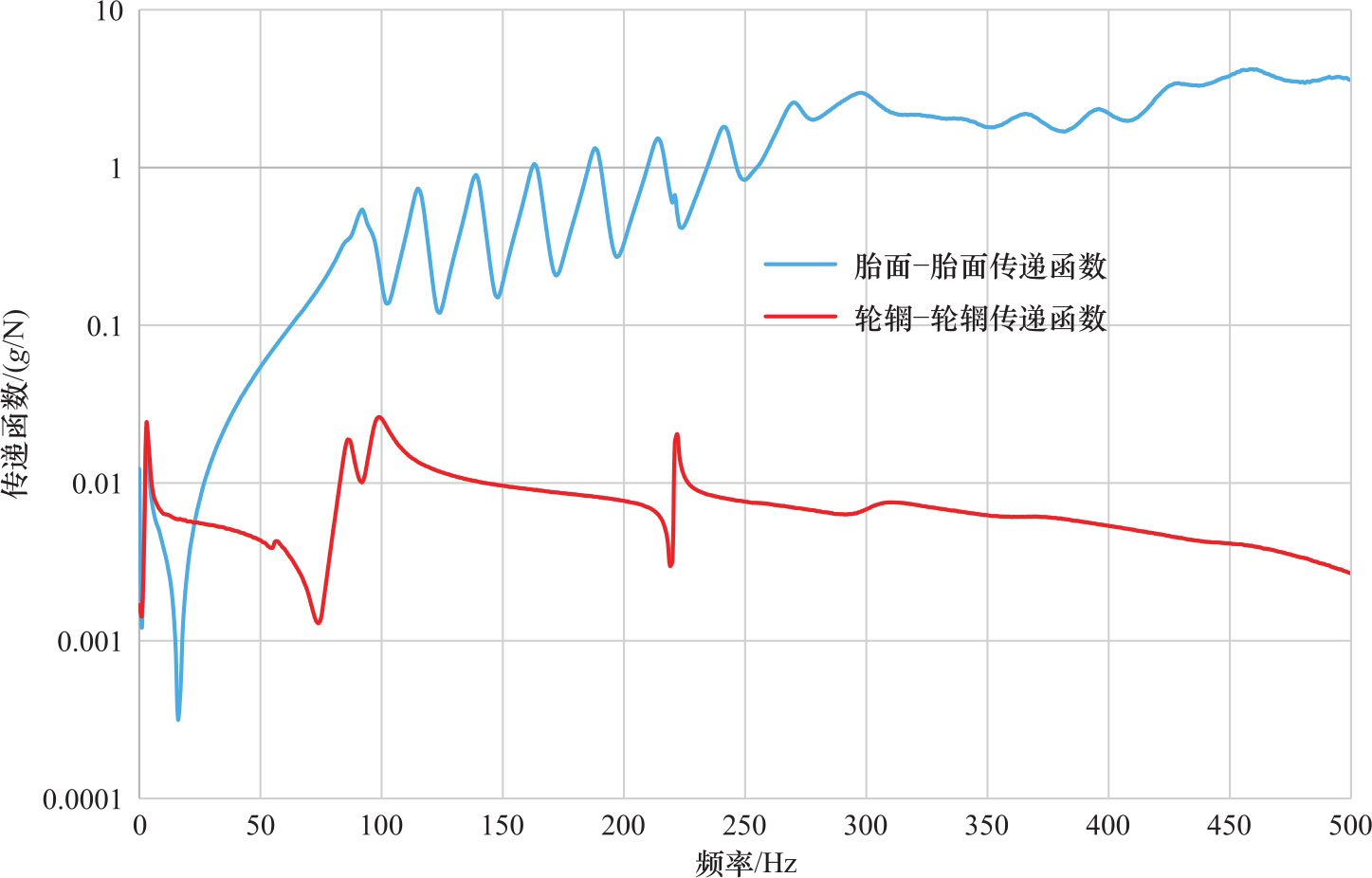
图3.3 胎面-胎面传递函数和轮辋-轮辋传递函数
众所周知,轮胎是一个非线性结构。轮胎的非线性体现在以下几个方面。
第一,橡胶是超弹性非线性材料,还具备黏弹性特征。发动机橡胶悬置和底盘橡胶衬套就是典型的例子,图3.4给出了它们的刚度曲线。在一定载荷下,刚度是线性的,这段载荷-位移区域被称为线性区域;当载荷超过一定值,载荷和位移之间不存在线性关系,即刚度进入非线性区域。因此,以橡胶为主体的轮胎也是非线性结构。
第二,胎体内部的帘线层和带束层材料是各向异性,其结构呈非线性。
第三,轮胎是由橡胶、帘线、钢丝等组成的一体,整体上是一个非线性结构。
第四,橡胶胎和金属轮辋结合,在外界载荷作用下,它们的变形不一致导致了结构呈现非线性特征。
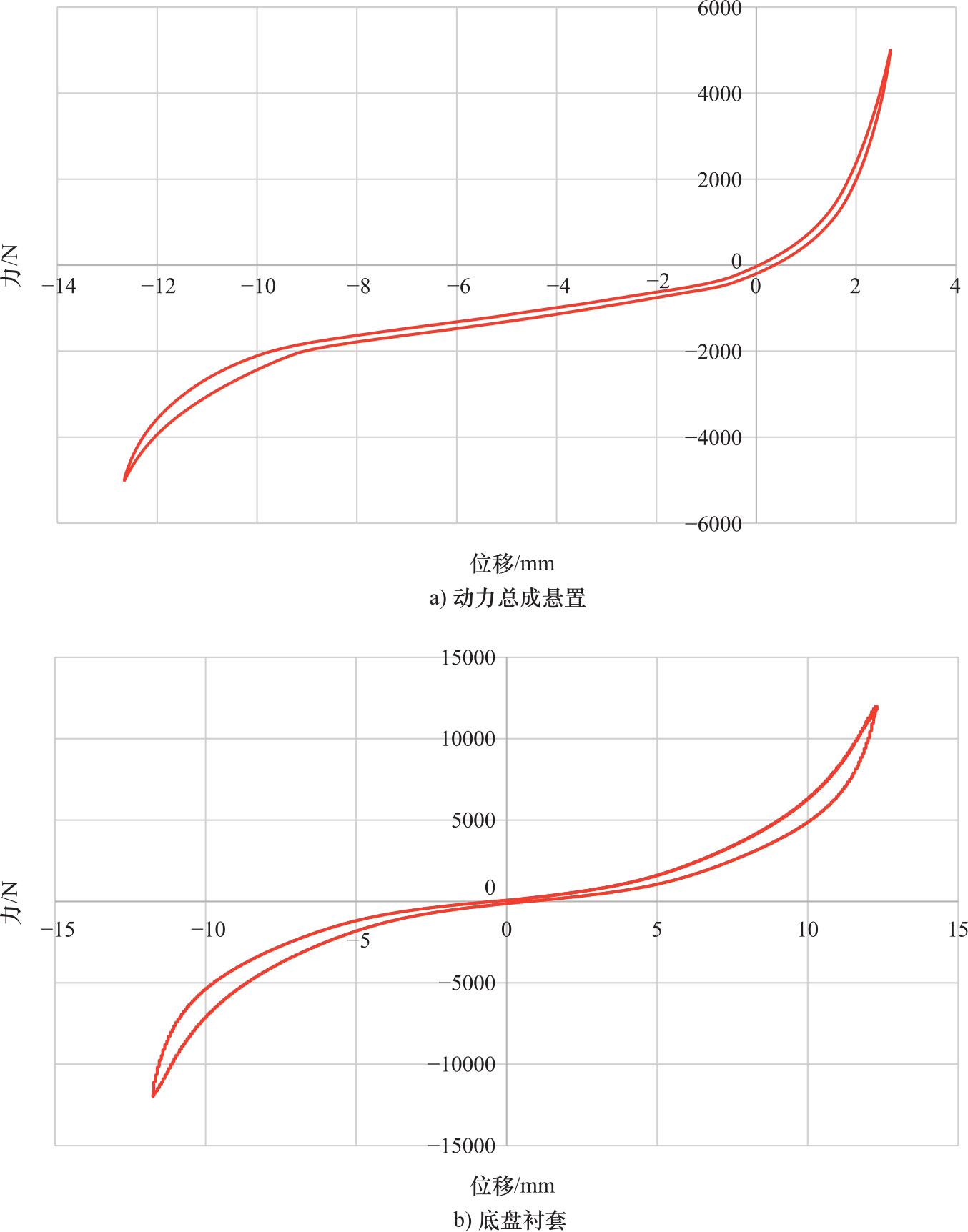
图3.4 橡胶载荷-位移曲线
非线性系统求解和分析非常复杂。因此,将一个非线性结构用线性方法来描述和分析是工程界的期望。在一定范围内和一定条件下,非线性结构分析可以简化成线性分析,很多困难问题就迎刃而解。
在工程实践中,下面几种现象或数据或许能帮助我们来假设轮胎是线性结构。
1)进行模态试验时,用小型激励器或者力锤来激励轮胎。对自由状态下的轮胎,激励力只有控制在一定范围内,才能保证它处于静止状况。如果激励力大,轮胎会移动,从而无法得到轮胎模态。图3.2和表3.1给出的胎面与轮辋之间的传递函数表明轮胎是线性结构。
2)图3.5是测得的一个轮胎的载荷-位移曲线和静态刚度-位移曲线。在大于5000N压力下,静态刚度接近线性。多数乘用车的质量小于2000kg,即每个轮胎承受的静态力小于5000N。在这样的压力下,轮胎显现出近似线性特征。
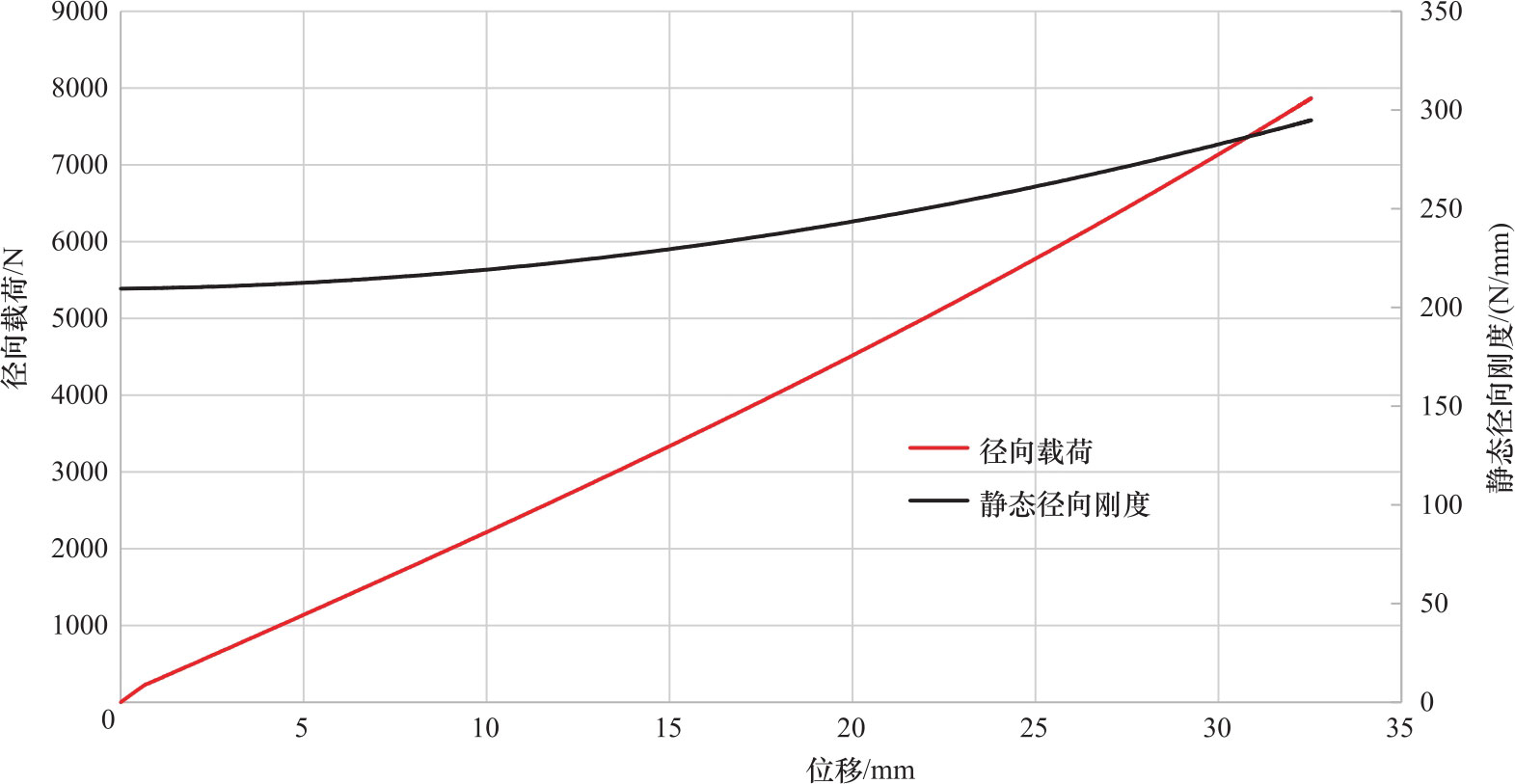
图3.5 一个轮胎的载荷-位移曲线和静态刚度-位移曲线
3)汽车在常用路面(光滑沥青路面、粗糙沥青路面和水泥路面)上行驶时,轮毂所承受的动态力比较小。用传递率可以从轮毂受力推算出轮胎承受的路面激励,它属于小激励,可以推测轮胎具备线性特征。当然,在轮胎受到大激励时,如汽车通过冲击路面、破损路面、隔离带等情况,由于激励大,轮胎会表现出非线性特征。
4)许多案例显示采用线性方法求解轮胎有限元模型,得到的模态频率和振型与试验得到的结果非常接近(冯希金等,2013;Brinkmeiera et al., 2008;Chern et al., 2006;Constant et al., 2001;Diaz et al., 2016;Kido et al., 2011;Lee et al., 2003;Wheeler et al., 2005;Yi et al., 2019;Yum et al., 2007)。表3.2给出了一个案例,以此推断轮胎线性假设是合理的。
表3.2 某个轮胎有限元计算与试验测试的模态频率对比(冯希金等,2013)

5)在验证有限元模型时,在轮胎上施加载荷,计算下沉量,得到载荷-下沉量曲线。通过比较试验测量值和有限元计算值来判断有限元模型的准确性,很多案例表明两者的差异在3%之内,曲线与图3.5类似,接近线性。因此,从工程的角度来看,可以把轮胎视为线性结构。
6)在进行理论分析时,许多学者将轮胎简化成“壳-环”(shell-ring)这样的线性模型,即胎面为“壳”,胎侧为“环”(Heckl,1986;Huang et al., 1987a;Huang et al., 1987b;Kim et al., 2007a;Kropp, 1999;Kung et al., 1986;Lecomte et al., 2010a;Liu et al., 2018;Matsubara et al., 2011;Matsubara et al., 2013a;Matsubara et al., 2013b;Matsubara et al., 2015;Wei et al., 2009;Yu et al., 2019)。理论计算值与试验值接近,由此也可以假设轮胎为线性结构。
基于以上的现象和数据,在分析和测试乘用车轮胎时,可以将它们近似地视为线性系统。但是如果轮胎受到大冲击载荷,如在严重破损的路面上行驶、穿越隔离带和缓冲带,轮胎线性假设不成立。