




PH分布 [1 -2] 是在有限状态马尔可夫链下达到吸收态前的时间分布。在状态空间中定义一个在时间上连续、在状态上离散的马尔可夫过程。假设状态空间为{1,2,3,⋯, m , m +1} ,令状态 m +1为吸收态、状态{1,2,⋯, m } 为非吸收态。( α , α m +1 ) 是马尔可夫过程的初始概率向量,其中 α =( α 1 , α 2 ,⋯, α m ) ,且满足 α e + α m +1 =1。将该过程的状态无穷小生成元定义为
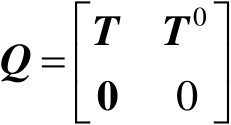
(3.1)
式中, T 为非吸收态{1,2,⋯, m } 的状态转移矩阵,是一个非奇异的方阵,由连续型马尔可夫过程的原理可知,其对角线元素均为负数,非对角线元素均为非负数; T 0 为非负列向量,是从任意状态到达 m +1状态的吸收概率(转移速率), Te + T 0 =0, e 是元素均为1的列向量。
假设在[0,∞)上的连续分布是PH分布,以( α , T )的形式表示,其中 α 表示非常返状态的初始概率向量; T 表示非常返状态之间的转移概率矩阵,且 T 的维数表示该分布的阶数,PH分布的概率密度函数 f ( x )和累积概率函数 F ( x )为
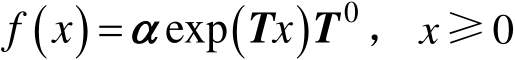
(3.2)
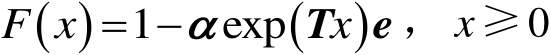
(3.3)
为了更好地表达PH分布的思想,通过系统状态转移图来对PH分布的 Q 矩阵进行解释,如图3.1所示。
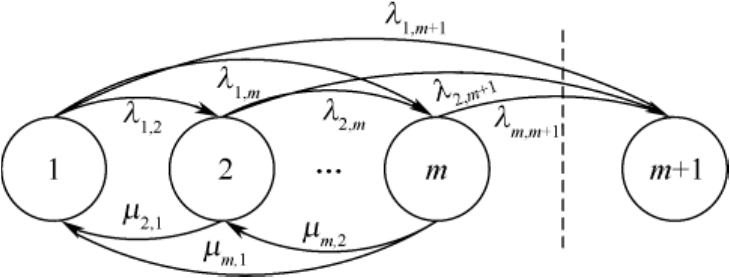
图3.1 系统状态转移图
系统进入吸收态前的工作时间服从PH分布,该过程的状态无穷小生成元为
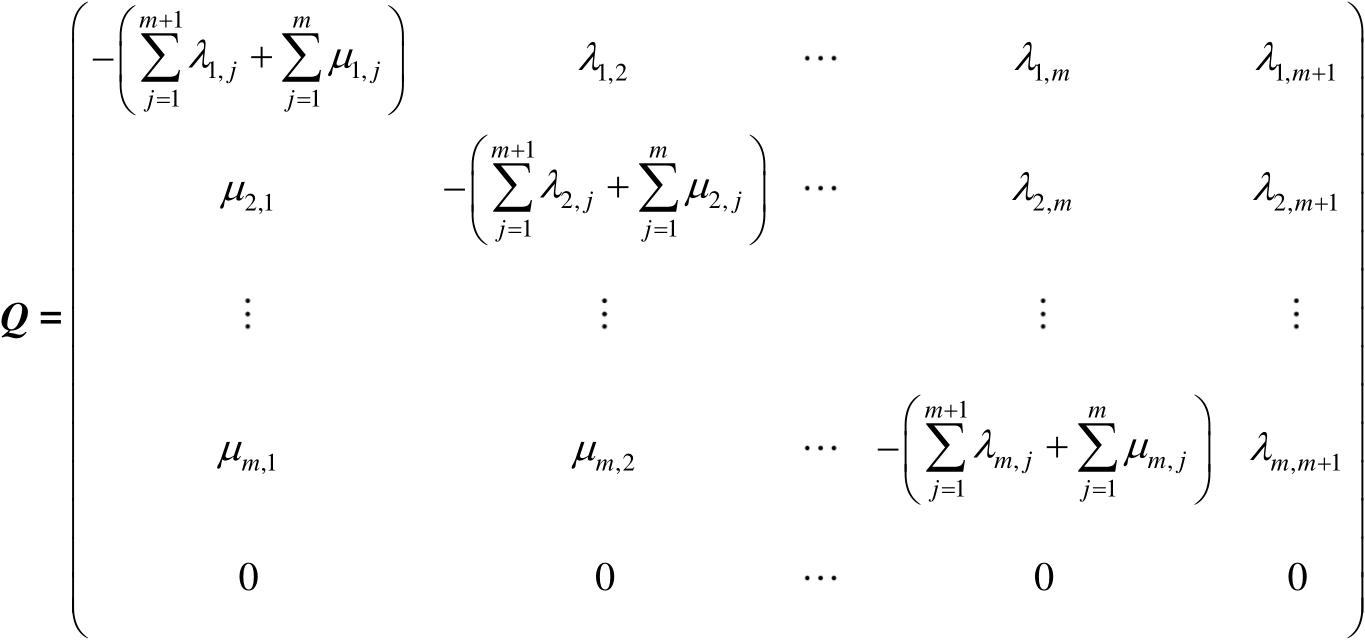
(3.4)
式中,
λ
i
,
j
为故障率;
μ
i
,
j
表示恢复速率;
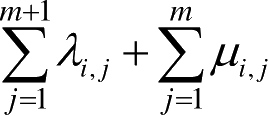 表示矩阵中每行的故障率与恢复速率之和,其中
i
≠
j
。
表示矩阵中每行的故障率与恢复速率之和,其中
i
≠
j
。