




离散型概率和连续型概率是统计学的基石。有许多经典的数学问题内含着统计知识。本节选择了3个典型问题,向读者详细介绍了概率是什么,以及如何在实际生活中应用它们。
三门问题出自一档美国电视节目。在节目中,舞台上放着3扇关闭的门,其中一扇门后有一辆豪车,另外两扇门后分别是一头山羊。玩家选择一扇门后,主持人会在其余两扇门中打开一扇有山羊的门,并询问玩家是否更换选择。
请问玩家是否应该更换选择呢?不更换将有多大可能选中跑车?更换又有多大可能?
当主持人打开一扇有山羊的门后,留给玩家选择的是两扇关闭的门,似乎无论玩家是否更换选择,选中跑车的可能性都是1/2,但只需具备最基础的统计学知识,就可知道正确结果并非如此,当玩家不更换选择时,有2/3的概率选中跑车;反之,只有1/3的可能选中跑车。
不妨将3扇门分别标号,并假设跑车放在1号门后,此时玩家选择每扇门的可能性是均等的。当玩家选择1号门时,无论主持人打开哪扇门,玩家更换选择时会选中山羊,不更换选择时会选中跑车;当玩家选择2号门时,主持人只能打开3号门,则玩家更换选择时会选中跑车,不更换选择时会选中山羊;玩家选择3号门时的情形与选择2号门时的情形类似。
表1.1列出了所有的情形及它们发生的概率。
表1.1 三门问题情况罗列
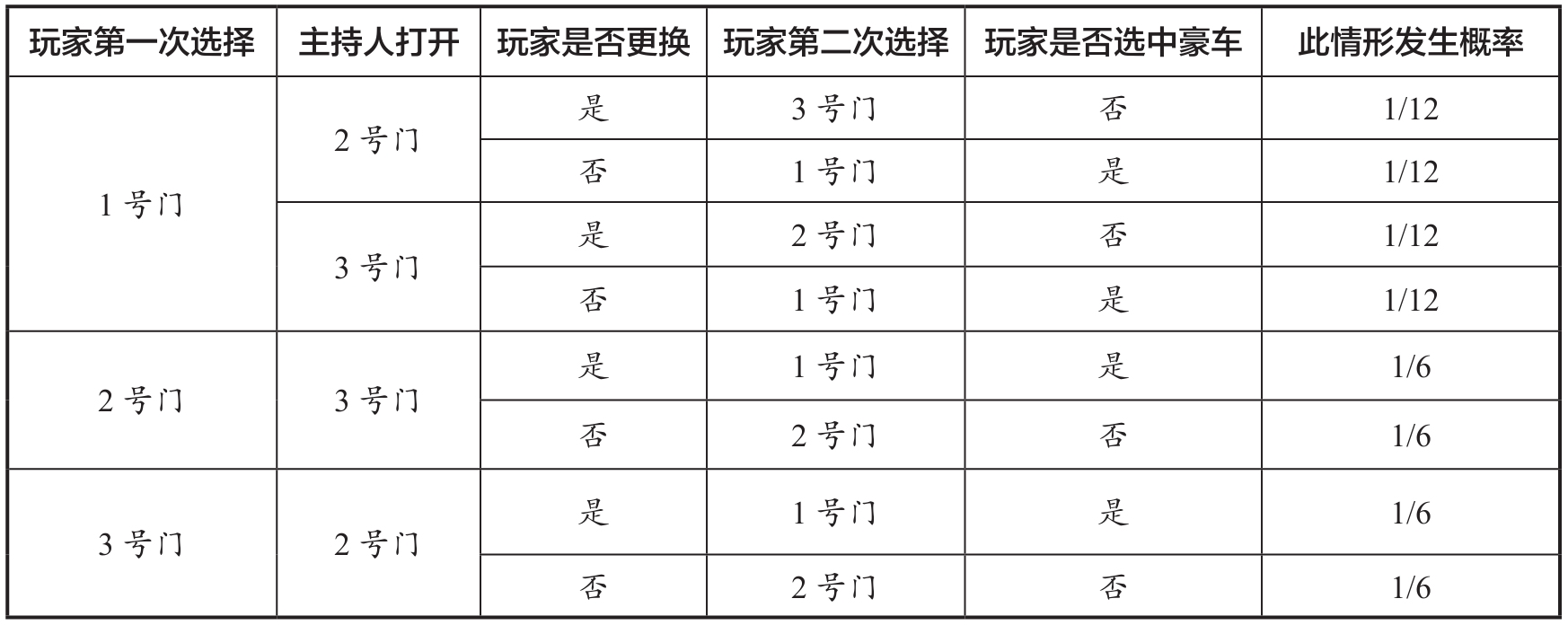
由于玩家选择1号门时,主持人既可打开2号门,又可打开3号门,并且打开这两扇门的概率相等,因此表1.1前4行的发生概率分别是1/12。而玩家选择2号门或3号门时,主持人只有一个选择,因此表1.1后4行的发生概率分别是1/6。
由表1.1即可汇总得出玩家是否更换选择与玩家是否选中豪车这两种情况的组合概率。结果如表1.2所示,玩家更换选择时选中豪车的概率是未选中豪车概率的两倍,即有2/3的概率选中豪车;未更换选择时选中豪车的概率是未选中豪车概率的一半,即有1/3的概率选中豪车。
表1.2 更换选择与选中豪车概率表

这样一个计算结果是不是出乎你的意料呢?罗列表格正是统计学的一项看家本领,这项工作需要细心、耐心,不能错漏数据。无论什么统计问题,正确、整齐的数据表格都是一个重要的开始。
三门问题的另一个解题关键便是主持人并不是随机打开一扇门的,而是一定打开一扇有山羊的门。如果读者懂得条件概率和全概率公式,就不需要罗列上述复杂表格,仅列出几个公式,便可得到正确答案。这两个统计知识也可以应用到许多其他问题上,可参阅7.3.2小节获得更详细的内容。
将统计数据罗列成表格有利于概览一个事件的全貌,从而解决实际问题。不过在罗列数据时,有一些常见的谬误却是不为大众所知的。以下是两个典型例子。
已知有一种罕见疾病的发病率是1%,这种疾病的检测方法的准确率是99%,小明被检测出罹患这种疾病,请问他真正患有这种病的概率是多少?
不妨假设做检查的一共有1万人,那么其中得病的人就有100人。9900个健康人去做检查时,将有99个人被检测出患病,而100个病人去做检查时会有一个人的检测结果是健康。
如表1.3所示,检测结果为患病的人总共有198人,其中有50%的人实际上是健康的,即小明实际上健康的概率是50%。与此类似,检测结果为健康的人总共有9802人,其中只有一人实际上患病,则对于检测结果为健康的人而言,检测错误的概率是0.01%。
表1.3 检测结果与真实情况统计表

读者可能对这个结果感到惊异。但在实际情况中,大多数医学检测的准确率都不能达到100%。因此对于罕见病来说,往往需要进一步的精确检测才能得知是否真的生病了。知道了这一点,也就无须对发生在身边的误诊感到诧异了。
另一个例子则与数据分组合并有关。医药公司对一种新药进行了双盲实验,实验组和对照组分别招募到120名志愿者,均划分为儿童组、少年组、成年组和老年组4个组别。结果发现单独对照各个组别时,对照组的痊愈率高于实验组,可是观察总体水平时,实验组的痊愈率又高于对照组。
表1.4所示是双盲实验具体数据。
表1.4 双盲实验具体数据
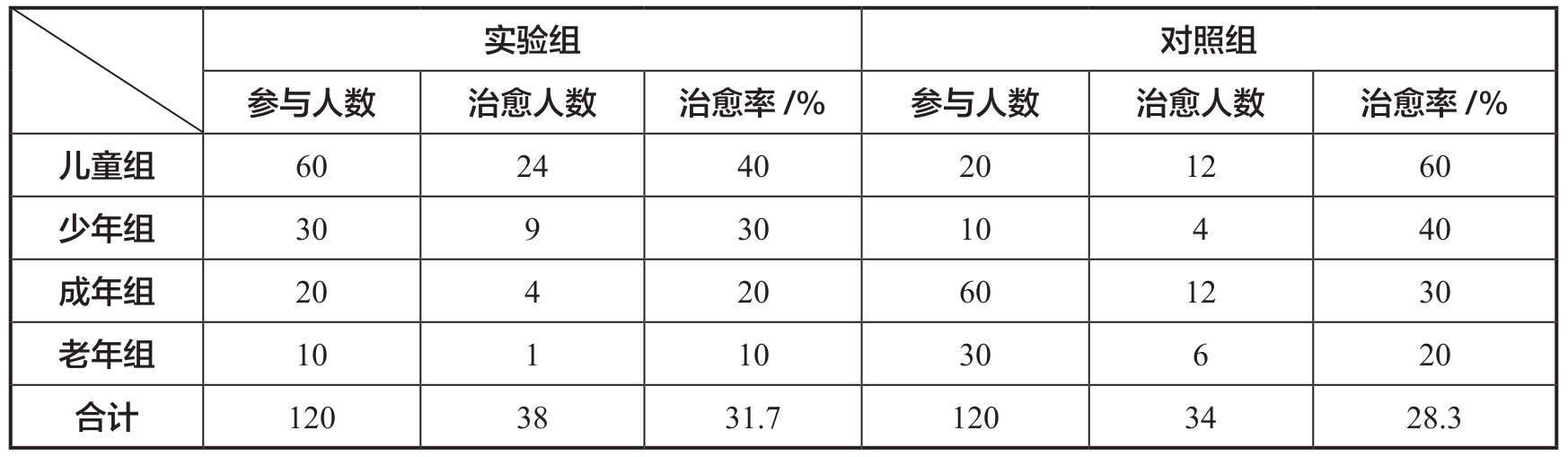
如表1.4所示,统计数据与上述奇怪现象吻合。仔细观察表1.4,不难发现实验组中儿童和少年的数量比对照组多,成年人和老年人的数量又比对照组少。由于儿童和少年的自愈能力较强,因此在合计总数时,实验组的治愈率也就不足为奇了。这个实验明显违反了基本的设计原则,即各个组别的人数应对等这一条件,最终结果掩盖了真实情况,即这种新药不但对患者无效,甚至可能有害。
在实际生活中,类似的统计疏漏、错误比比皆是,有时数据处理人出于某种目的会故意误导读者。例如,出现在广告中的统计数据往往会经过美化。有时真实数据有较多的“陷阱”,稍微粗心便会得出错误的结论。读者可参阅第2章和第3章的内容,了解更多有关统计数据的秘密。第4~8章则列举了许多化腐朽为神奇的优秀案例。
除前述几个较为浅显的统计问题外,还有一些问题应用了更为深奥的统计知识。例如,下面这个问题。
波斯有位美丽的公主,她要在100个候选人中挑选自己的丈夫。候选人依次从公主面前经过,公主同一时间只能见一个人,离开公主房间的人不能再回去。当公主选择某一个人后,后面的人都不能再面见公主。如果前99个人在经过公主房间时,公主都没有选择,那么她就必须选择最后一个人。
这是个颇具趣味的数学问题,困难的地方就在于候选人不能回头。如果能够回头,这个问题是很好解决的,公主只需把所有的候选人都看一遍,再回头挑选最心仪的那个人就可以了。
不妨再简化一下这个问题,将公主对每个候选人的心仪程度量化为一个数值,则我们的任务就是帮助公主选择心仪值最高的候选人。
由于候选人不能回头,因此就不能根据她没见过的候选人的好坏来决定选哪个人,只能根据她已见过的候选人的好坏来下决定。当公主还没开始面见候选人时,她对于候选人是一无所知的,见的候选人越多,对全体候选人的了解也就越多。
公主既不能在一无所知时就下决定,又不能面见全部候选人后再下决定,因此公主只能先观察一部分候选人,再根据这部分候选人的情况挑选丈夫。不妨假设公主先面见了一半的候选人,则此时已产生了一个最大心仪值,那么只要之后出现一个比它更大的心仪值,公主就应毫不犹豫的选择他。
但是这种做法有明显的缺陷。最佳候选人有一半的概率出现在候选人队列的前半段,也就是说,公主有一半的概率不得不嫁给最后一个人,可倘若公主只看了1/10的候选人就匆匆下决定,就有可能与最佳候选人失之交臂。
那么公主观察多少人就开始挑选丈夫比较好呢?
一共有100个候选人,不妨假设公主一共观察了 k 个候选人,这 k 个候选人也就是候选人队列中最前面的 k 个。最佳候选人可能的位置就有100个,落在每个位置上的概率都是1%。
如果最佳候选人位于前 k 个位置,那么公主就只能嫁给最后一个人,这件事发生的概率是 k %。如果最佳候选人的位置特别靠后,而前 k 个候选人又都不心仪,那么公主可能会在遇到最佳候选人前就选了另一个较好的,但不是最好的候选人。
下面从统计学角度解题。
用 i 代表最佳候选人的位置,只有在 i 大于 k ,而且前 i -1个候选人中的最佳候选人位于前 k 个候选人之中时,公主才能选到最佳丈夫。那么对于某个固定的 k 来说,选到最佳候选人的概率就是:
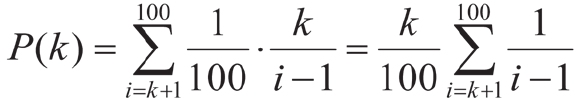
我们希望能找到一个 k ,使 P ( k )达到最大。不妨令 k 分别等于从1~100中的每一个整数,经过100次计算,即可发现当 k 等于37时, P ( k )达到最大。也就是取前37个候选人作为观察对象时,选到最佳候选人的概率最大,这个概率大约为40%,还有60%的可能不得不选择最后一个,或者没有选到最佳的候选人。
考虑更广泛的情景,不妨使用 n 来代表候选人的数量,那么对于某个固定的样本数来说,选到最佳候选人的概率就是:
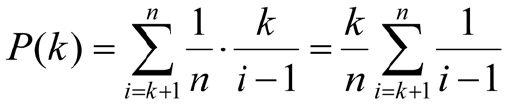
用 x 来表示 k / n 的值,并且假设 n 充分大,则上述公式可以写成:
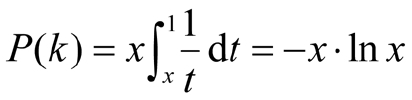
对- x ·ln x 求导,并令这个导数为0,可以解出 x 的最优值,也就是1/e,约为37%。e是自然常数,其值约为2.71828。以 n 来代表候选人个数,则取 n /e个候选人作为观察对象是最恰当的。
不过,即便找到样本数的最优解,也仍只有约40%的概率选到最佳候选人,约23%的概率选到较好的候选人,还有约37%的概率不得不选择最后一个候选人。
波斯公主选驸马这个问题意味着这样一个事实,只需一小部分观察对象就可推断出全部观察对象中的信息,即37%的样本即可代表整体。这个问题可以泛化为一切寻找总体最优值的问题,而部分代表整体的思想也正是统计学的奠基思想。