无人机运动模型的建立是无人机单机控制的基础,主要涉及坐标系选择、运动参数确定和无人机运动方程建立等方面。
作用在无人机上的重力、发动机推力和空气动力及相应力矩的产生原因是各不相同的,因此,为了确切地描述无人机的运动状态,选择合适的坐标系来描述无人机的空间状态是非常重要的。例如,要想确定无人机在地球上的位置,则采用地面坐标系比较方便;要想描述发动机的推力,则采用机体坐标系比较方便;要想描述空气动力,则采用气流坐标系比较方便。
由此可见,合理地选择不同的坐标系来定义和描述无人机的运动参数,是建立并分析无人机运动模型的重要基础。通常情况下,无人机运动模型的参数是定义在不同坐标系上的,所以在建模过程中通过坐标系变换进行向量的投影分解是不可避免的。因此,本小节主要介绍常用坐标系和坐标系之间的变换的相关内容。
地面坐标轴系(地轴系)为S g –O g X g Y g Z g 。地面坐标轴系是相对于地面不动的坐标系。原点O固定在地面的某点,X g 轴在水平面内并指向某一方向,Z g 轴垂直于地面并指向地心,Y g 轴也在水平面内,并垂直于X g 轴,其指向按右手定则确定。一般在建立无人机运动方程时,忽略地球的旋转和曲率,把地面坐标轴系看成惯性坐标系,如图3-1所示。
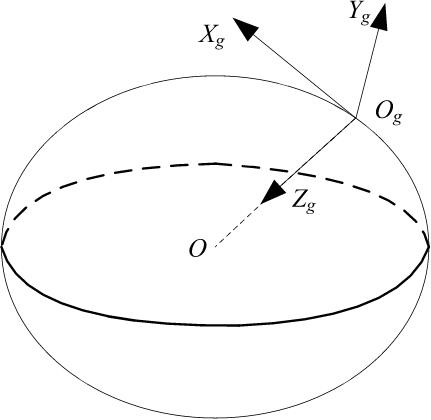
图3-1 地面坐标轴系
机体坐标轴系为S b –O b X b Y b Z b 。机体坐标轴系是与无人机固定相连的坐标系。原点O在无人机的重心上,X b 轴在无人机对称平面内平行于无人机的设计轴线并指向机头,Y b 轴垂直于无人机对称平面并指向机身右方,Z b 轴在无人机对称平面内,与X b 轴垂直并指向机身下方,如图3-2所示。机体坐标轴系主要用来描述无人机相对于该轴系的受力和运动关系。
气流坐标轴系为S a –O a X a Y a Z a 。气流坐标轴系与无人机固定相连。原点O在无人机的重心上,X a 轴与飞行速度V一致,Z a 轴在无人机对称平面内与X a 轴垂直并指向机腹下方,Y a 轴垂直于O a X a Z a 平面并指向机身右方。气流坐标轴系也称为速度坐标系。
稳定性坐标轴系为S s –O s X s Y s Z s 。稳定性坐标系与无人机固定相连。原点O在无人机的重心上,X s 轴与飞行速度V在无人机对称平面内的投影重合,Z s 轴位在无人机对称平面内与X s 轴垂直并指向机腹下方,Y s 轴与机体轴Y重合一致。
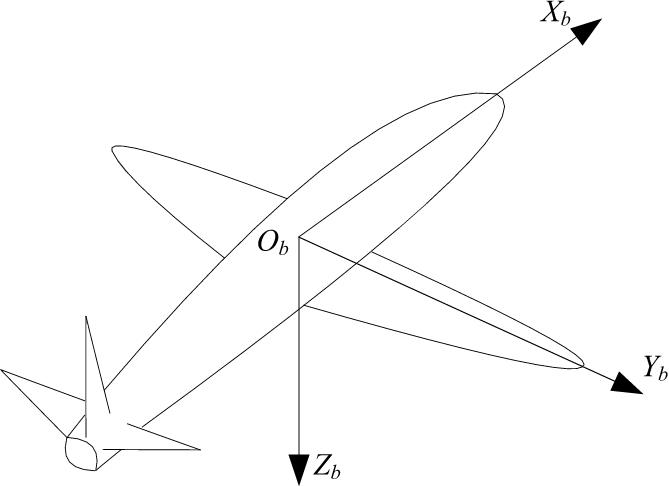
图3-2 机体坐标轴系
为了方便地描述无人机相对于地面的运动,需要确定机体坐标轴系、气流坐标轴系以及稳定性坐标轴系等动坐标系相对于惯性坐标系(地面坐标系)的方位,同时各动坐标系之间也需要确定彼此的相对方位。另外,为了使作用在不同坐标系中的力统一到选定的坐标系中,并由此建立沿着各个轴向的力的方程以及围绕各轴的力矩方程,必须知道各个坐标系之间的转换关系。
一般来说,任何一组直角坐标系相对于另一组直角坐标系的方位,都可以由欧拉角来确定。下面以地面坐标轴系和机体坐标轴系的转换为例,来说明各坐标系之间的转换。
假设经过坐标平移,两坐标轴系的原点重合于无人机的重心O点,然后经过三次旋转来实现两坐标轴系之间的转换,如图3-3所示。
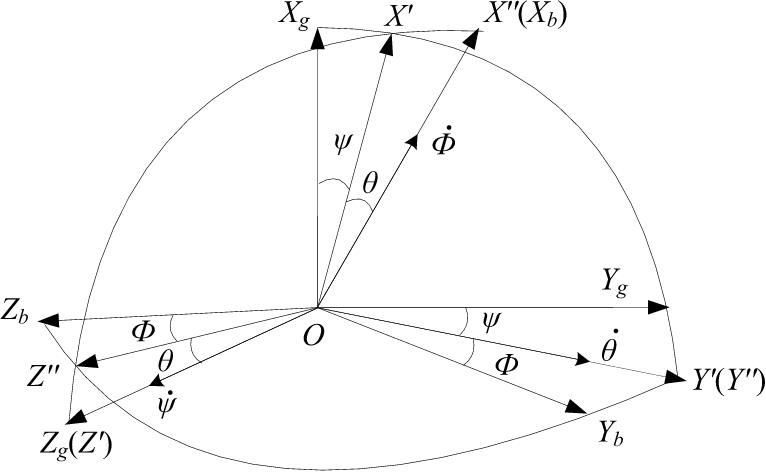
图3-3 欧拉变换
由地面坐标轴系S g 转动偏航角ψ到过渡坐标轴系S'–OX'Y'Z',即式(3-1)。

由过渡坐标轴系S'转动俯仰角θ到过渡坐标轴系S″–OX″Y″Z″,即式(3-2)。

由过渡坐标轴系S″转动滚转角Φ到机体坐标轴系S b –O b X b Y b Z b ,即式(3-3)。

由地面坐标轴系S g 到机体坐标轴系S b 的转换矩阵为式(3-4)。
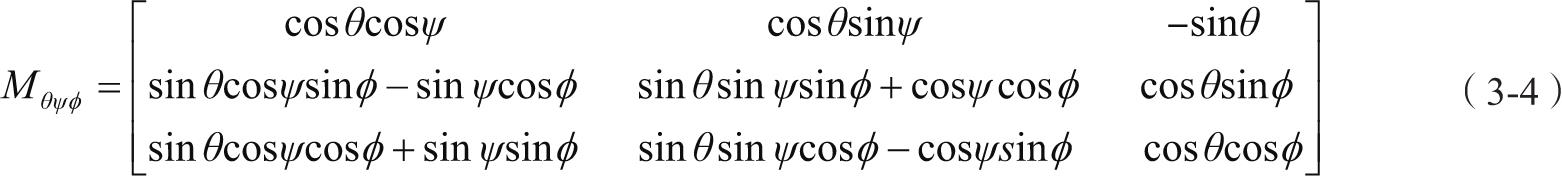
所以,地面坐标轴系与机体坐标轴系之间的转换满足方程式(3-5)。

采用同样的方法,可以进行其他坐标轴系之间的转换。
无人机的运动参数用来完整描述其运动所需要的变量。只要这些参数确定了,无人机的运动也就唯一确定了。因此,可以把无人机的运动参数看成是飞行自动控制系统中的被控量。
无人机的姿态角是由机体坐标轴系与地面坐标轴系之间的关系确定的,即通常所指的欧拉角。
(1)偏航角ψ:机体轴X b 在地平面上的投影与地轴X g 之间的夹角,以机头右偏航时为正。
(2)俯仰角θ:机体轴与水平面的夹角,以机头抬起时为正。
(3)滚转角Φ:机体轴Z b 与通过机体轴X b 的铅垂平面之间的夹角,以无人机右滚时为正。
气流角又称气动角,是由飞行速度向量与机体坐标轴系之间的关系确定的。
(1)迎角α:飞行速度向量V在无人机对称平面内的投影与机体轴X之间的夹角,V的投影在机体轴X b 下面时为正。
(2)侧滑角β:飞行速度向量V与无人机对称平面之间的夹角,V的投影在对称平面右侧时为正。
无人机的航迹角是由气流坐标轴系与地面坐标轴系之间的关系确定的。
(1)航迹倾斜角μ:飞行速度向量V与水平面的夹角,以无人机向上飞时为正。
(2)航迹方位角φ:飞行速度向量V在水平面上的投影与地轴X g 之间的夹角,投影在X g 右侧时为正。
(3)航迹滚转角γ:速度轴Z a 与通过速度轴X a 的铅垂面之间的夹角,无人机向右滚转时为正。
另外,还会用到以下变量符号。
(1)u、v、w:无人机在静止空气中的飞行速度向量在机体坐标轴系中的分量。
(2)p、q、r:无人机角速度在机体坐标轴系中的分量,分别为滚转角速度、俯仰角速度和偏航角速度。
(3)D、L、C:无人机所受空气动力在机体坐标轴系中的分量,分别为阻力、升力和侧力。
(4)L、M、N:无人机所受空气动力矩在机体坐标轴系中的分量,分别为滚转力矩、俯仰力矩和偏航力矩。
(5)T:无人机发动机的推力。
(6)m:无人机及其载荷的质量。
无人机在外力作用下的运动规律一般是用运动方程来描述的,即用微分方程的形式来描述无人机的运动和状态参数随时间的变化规律。无人机的运动方程通常可分为动力学方程和运动学方程,动力学方程以牛顿第二定律为基础建立,运动学方程通过坐标变换得出。
在惯性参考系中,应用牛顿第二定律可以建立起飞行器在外合力F作用下的线运动,以及在合力矩M作用下的角运动。
无人机在外合力作用下的线运动方程为式(3-6)。

无人机在外合力矩作用下的角运动方程为式(3-7)。

式中,F为外力,M为外力矩,m为无人机质量,v为无人机质心的速度向量,H为动量矩。
以机体坐标系为动坐标系,建立的动力学方程为式(3-8)和式(3-9)。
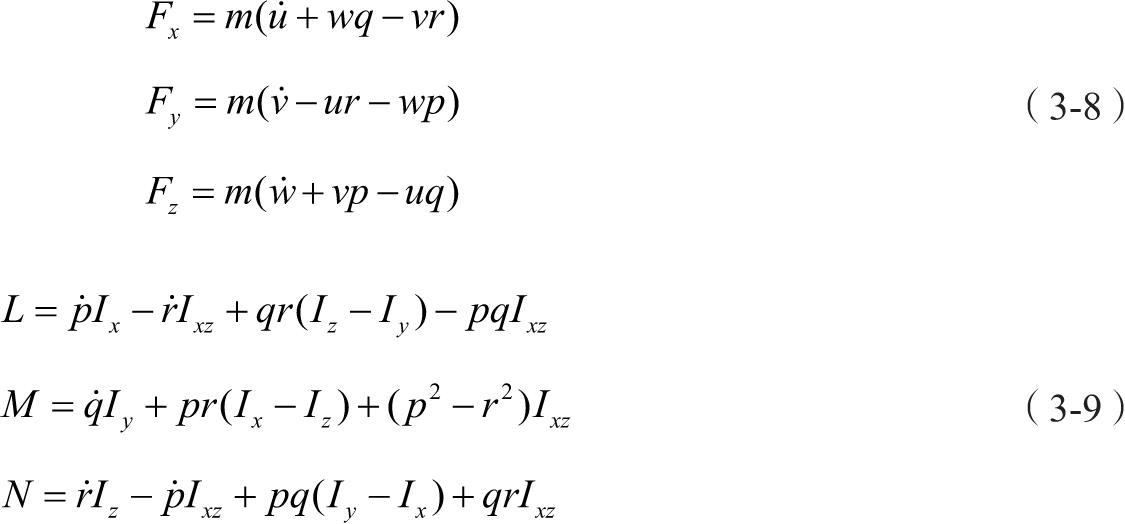
为了描述无人机相对于地面的运动,由动坐标系(机体坐标系)和地面坐标系之间的关系得到运动学方程式(3-10)和式(3-11)。
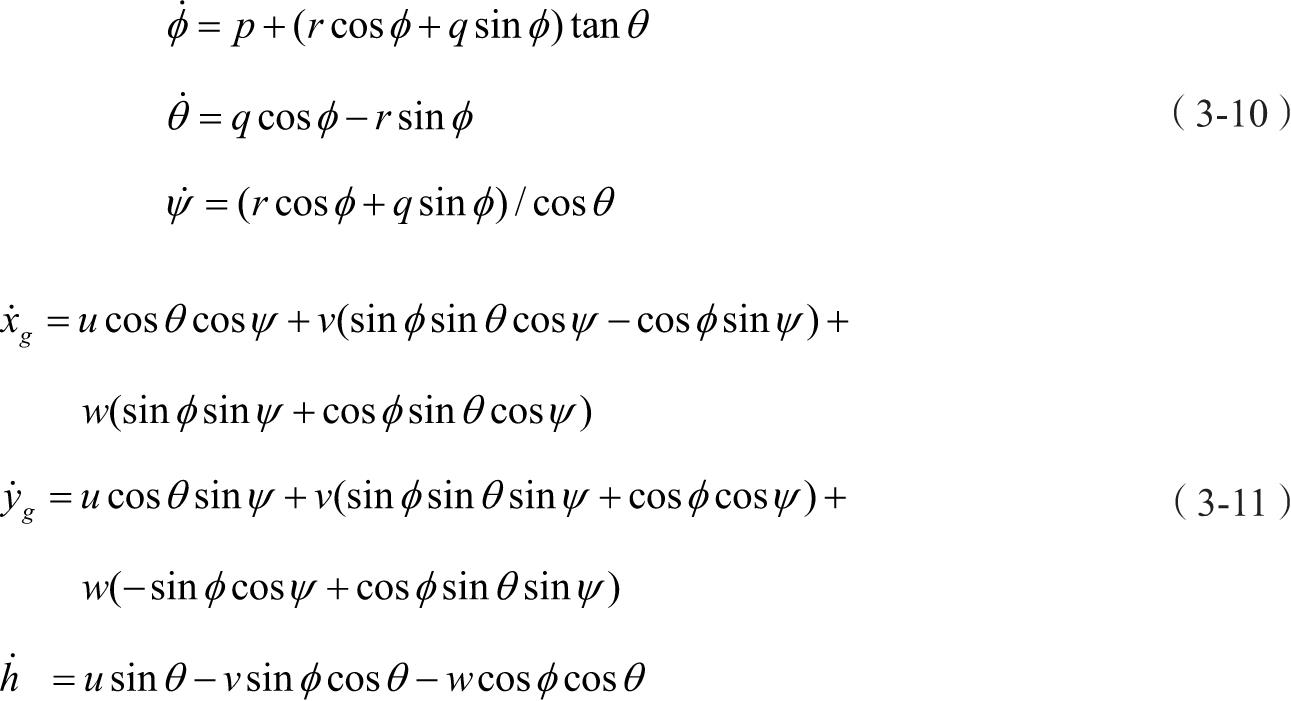
无人机的一般运动方程是一组复杂的非线性微分方程组,不利于分析构形参数与运动稳定性、操纵性等的内在联系,如果直接用其进行控制律设计会非常复杂,而线性化的运动方程更适合以成熟的线性系统控制理论为基础的飞行控制系统的设计。因此,在分析无人机的构形参数与飞行稳定性和操纵性之间关系以及设计飞行控制系统之前,将方程进行线性化处理的方法成为目前在实际工程中广泛应用的重要方法之一。小扰动法是将非线性方程线性化的一种方法,它得到的方程为小扰动方程。
在刚体飞行器运动的假设下,无人机在空间中的运动有六个自由度,即质心的三个移动自由度和绕质心的三个转动自由度。对无人机来说,质心的三个移动自由度是速度的增减运动、上下升降运动和左右侧移运动。三个转动自由度是俯仰角运动、偏航角运动和滚转角运动。由于无人机有几何和质量对称面,因此根据各自由度之间的耦合强弱程度,可以将六个自由度的运动分成对称平面和非对称平面内的运动。纵向运动(对称平面的运动)包括速度的增减、质心的升降和绕O y 轴的俯仰角运动;横侧向运动(非对称平面内的运动)包括质心的侧向移动、绕O z 轴的偏航角运动和绕O x 轴的滚转角运动。
在小扰动等基本假设条件下,飞机可以线性化为纵向运动方程和横侧向运动方程。通常情况下,可以利用升降舵、副翼、方向舵及油门来完成对飞机运动的控制。其中升降舵、副翼、方向舵及油门的偏转角分别用δ e 、δ a 、δ r 、δ T 表示,其方向规定如下。
(1)δ e :升降舵下偏为正。
(2)δ a :副翼左上右下为正。
(3)δ r :方向舵左偏为正。
(4)δ T :加油门为正。
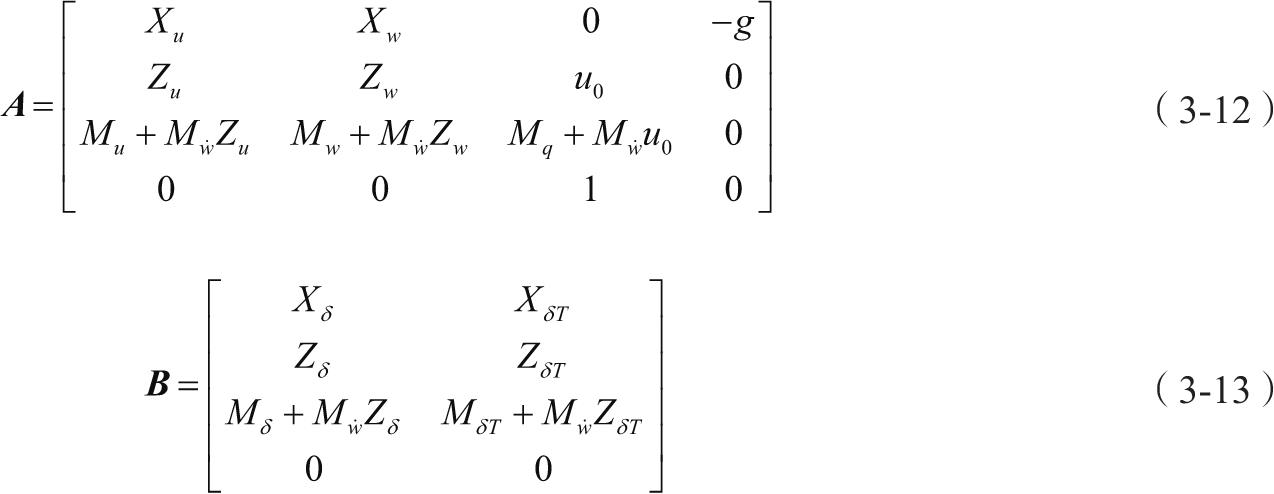
纵向线性化小扰动运动方程式的简化形式为: ẋ=Ax+Bη ,其中 x =[∆u ∆w ∆q ∆θ] T , η =[∆δ e ∆δ T ] T , x 为状态变量, η 为控制变量,矩阵 A 和 B 包含了飞机的有量纲的稳定性导数,如式(3-12)和式(3-13)。
横侧向线性化小扰动运动方程组的简化形式为: ẋ=Ax+Bη ,其中 x =[∆v ∆p ∆r ∆φ] T , η =[∆δ a ∆δ r ] T ,得到式(3-14)和式(3-15)。
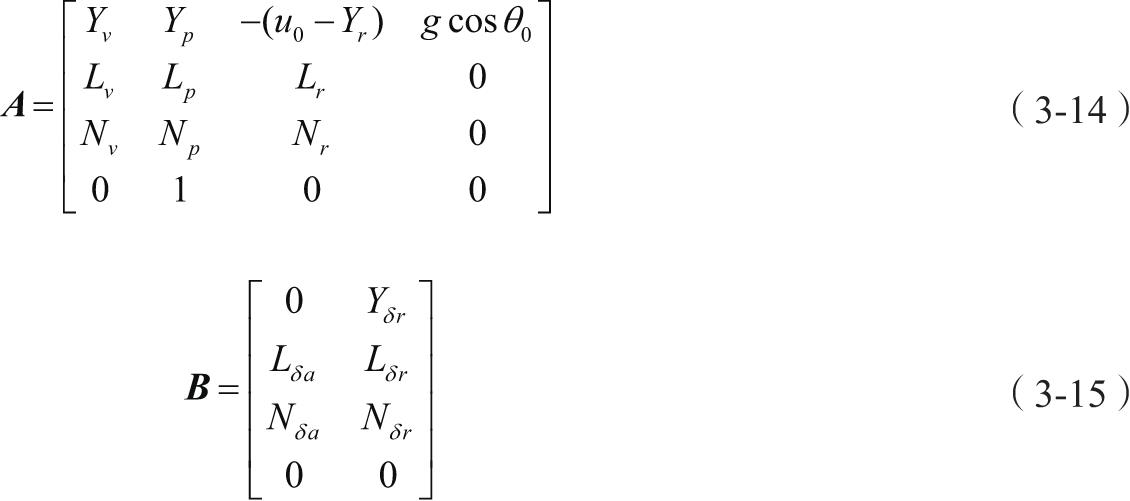
Aerosonde无人机气动布局合理,具有较高的静稳定性,以巡航状态点为设计点,利用Aerosim工具箱的线性化功能对非线性模型进行线性化处理。选取的基准运动为:无人机水平无侧滑飞行,速度v=25m/s,高度h=500m,滚转角φ=0,侧滑角β=0,迎角α=2.95deg,俯仰角θ=2.95deg,p=q=r=0。
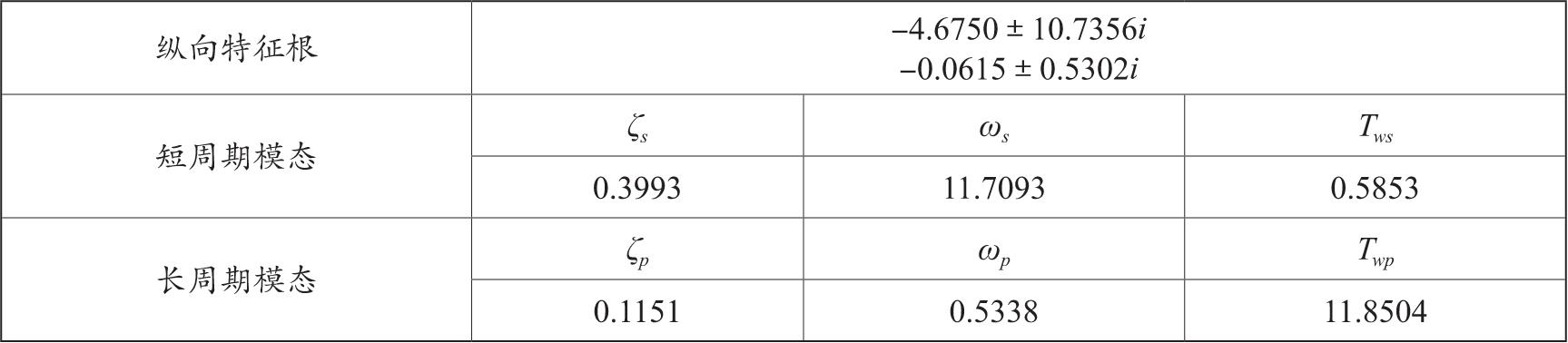
纵向运动线性化方程为:状态方程 ẋ=Ax+Bη ,输出方程 y=Cẋ ,其中 x =[u w q θ] T , η =[δ e δ T ] T , y =[Va a q θ] T ,得到式(3-16)、式(3-17)和式(3-18),纵向基本特性如表3-1所示。

表3-1 纵向基本特性
横向运动线性化方程为:状态方程 ẋ=Ax+Bη ,输出方程 y=Cẋ ,其中 x =[v p r φ] T , η =[δ a δ r ] T , y =[β p r φ] T ,得到式(3-19)、式(3-20)和式(3-21)。


常规飞机的横向动态特性用4个典型的扰动运动模态来表示,大负根表示快速滚转运动模态,小根表示缓慢运动螺旋模态,一对共轭负根表示荷兰滚运动模态,横向基本特性如表3-2所示。
表3-2 横向基本特性