二 联言命题和联言推理

联言命题是断定几种事物情况同时存在的复合命题，它的标准形式是“p并且q”，其中p、q称为联言支。在日常语言中，联言命题有多种表述形式。例如：

（1）3和117都是素数。

（2）韩娜结了婚，然后生了孩子。

（3）林纾是著名翻译家，但他不懂外语。

（4）林岗不但智力优秀，而且品德出众。

（5）即使他是一位穷人，他也努力保持自己的尊严。

这些分别表示并列、承接、转折、递进关系的复合命题，都是联言命题。在自然语言中，表示对偶、对比、排比关系的句子常常省略掉联结词。例如：

鸟宿池边树，僧敲月下门。

我们把“p并且q”看作联言命题的标准表达形式，其中p、q称为联言支。逻辑学研究命题是为了研究推理，从具体的推理抽象出一般的推理形式，其最重要的特性就是保真性：该推理形式本身能够确保从真前提推出真结论。因此，从推理的角度看命题，命题最重要的性质就是它的真值；就复合命题而言，则是一复合命题的支命题与该复合命题本身在真假方面的相互关系。就联言命题来说，只有它的各个支命题都是真的，它本身才是真的；如果有一个支命题为假，则联言命题为假。也就是说，一个联言命题是真的，当且仅当它的各个联言支都是真的。见下面的真值表：

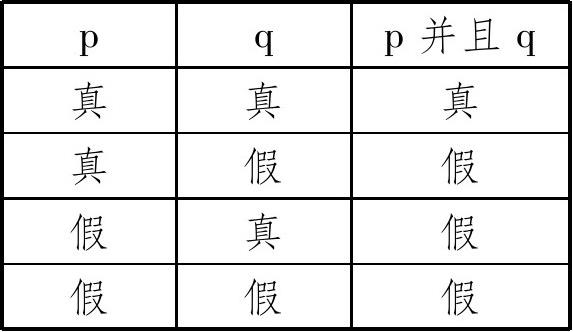
例如，联言命题“小张既高又胖”，只有在“小张高”和“小张胖”都真的情况下才是真的，在其余情况下则是假的。

根据联言命题的这种性质，联言推理的有效式包括：

1.合成式

若分别肯定两个联言支，则可以肯定由这两个联言支组成的联言命题。其形式是：

p

q

所以，p并且q

例如：“孔子是伟大的教育家，孔子是伟大的思想家，所以，孔子既是伟大的教育家又是伟大的思想家。”

这种推理在我们的日常思维中是经常使用的。例如，我们先分别论述某些观点成立，然后在文章结尾处加上“综上所述”“概而言之”“总而言之”等等，就是把前面所说的各点意思概括、综合起来。这就是在运用合成式推理。毛泽东在《中国社会各阶级的分析》这篇名文中就是采用这样的写作方式，前面分别论述地主阶级和买办阶级、中产阶级、小资产阶级、半无产阶级和无产阶级等等对中国革命的立场和态度，文末对全文的观点作一总结：

综上所述，可知一切勾结帝国主义的军阀、官僚、买办阶级、大地主阶级以及附属于他们的一部分反动知识界，是我们的敌人。工业无产阶级是我们革命的领导力量。一切半无产阶级、小资产阶级，是我们最接近的朋友。那动摇不定的中产阶级，其右翼可能是我们的敌人，其左翼可能是我们的朋友——但我们要时常提防他们，不要让他们扰乱了我们的阵线。

2.分解式

若肯定一个联言命题，则可以分别肯定其中的每一个联言支。其形式是：

p并且q

所以，p

或者

p并且q

所以，q

例如：“胡适是五四新文化运动主将，并且曾任北京大学校长；所以，胡适曾任北京大学校长。”

这种推理形式看似简单，其实不可或缺。例如，有时候，在前面有许多合成条件，但在后面的推理中只需要用到其中的某一个条件，分解式告诉我们，从前面的合成条件中可以得到这一简单条件，该推理于是可以进行下去。顺便说一下，逻辑学实际上是把我们日常思维中的一连串复杂的推理，分解为每一步都很简单的推理，这些推理受明确的规则控制，可以操作，可以检验。

3.否定式

若否定一个联言支，则否定包含这个联言支的联言命题。其形式是：

并非p

所以，并非（p且q）

例如：从“并非李白是一位著名的小说家”，可以推出：“并非李白既是伟大的诗人又是著名的小说家。” nkKNlAdwPF4QfufdYcfhDImwF6YyFYTXJp8TiKdxzH94DaluuqaPfMEQBeqb1566