




所谓的理想粗糙表面就是指表面由许多排列整齐的曲率半径和高度相同的粗糙峰组成,同时各峰承受载荷的变形完全一样,而且互相不影响。
如图 1.13 所示,着重考虑忽略微凸体的存在,设用完全平滑的表面压入这些微凸体,法向变形量 δ 等于( z - d ),微凸体间没有互相作用,因此一个微凸体发生变形时不会影响另一个微凸体的高度。假设所有微凸体的变形都相同,即它们在垂直载荷 W 的作用下同时下移一距离( z - d )。
若单位面积上有 n 个微凸体,则粗糙表面所支承的均匀分布的总载荷为 nW i ,这里 W i 为每个微凸体上所承受的载荷,如图 1.13 所示。根据赫兹分析,若以法向变形量 δ 来表示,则每个微凸体压痕的弹性接触半径 a 为:

接触面积 A e i 为:

载荷 W e i 为:

或令 δ = ( z - d ),有

而

总载荷 W e 和总的实际接触面积 A e 可从下式得出:

因为实际接触面积 A e = nA e i

则

可知,当接触为弹性时,实际的接触面积与所加法向载荷的 2 /3 次方成正比。
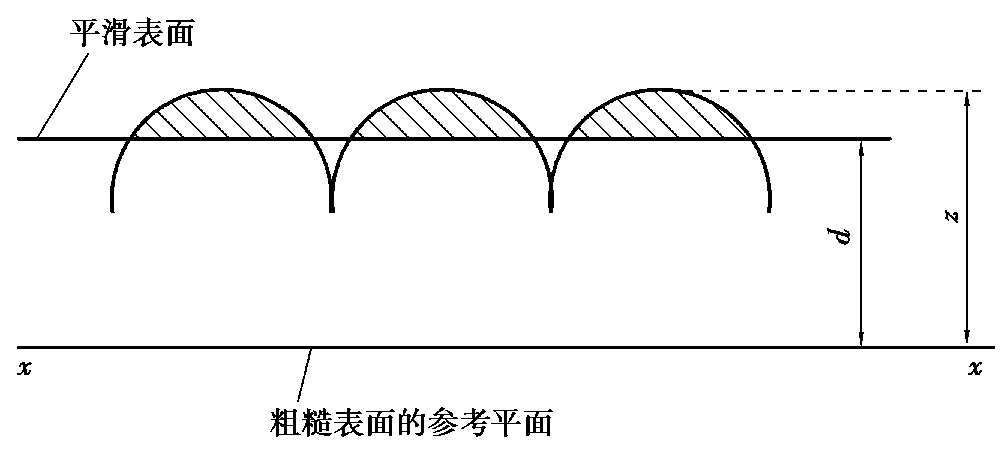
图1.13 等高球形粗糙表面的接触