




当两个固体表面接触时,由于表面存在粗糙度,假如上表面是光滑的,则载荷加在下表面的少数几个尖峰上,真实的接触面积只在微凸体顶部的几个点上;假如载荷低而且材料具有较高的屈服应力,则该接触是弹性接触。因此,在接触点上会发生塑性流动、黏着、冷焊等现象。这些情况都会发生在多数的摩擦界面上,而且金属材料的摩擦磨损过程均与真实的固体接触密切相关,如图 1.9 所示。
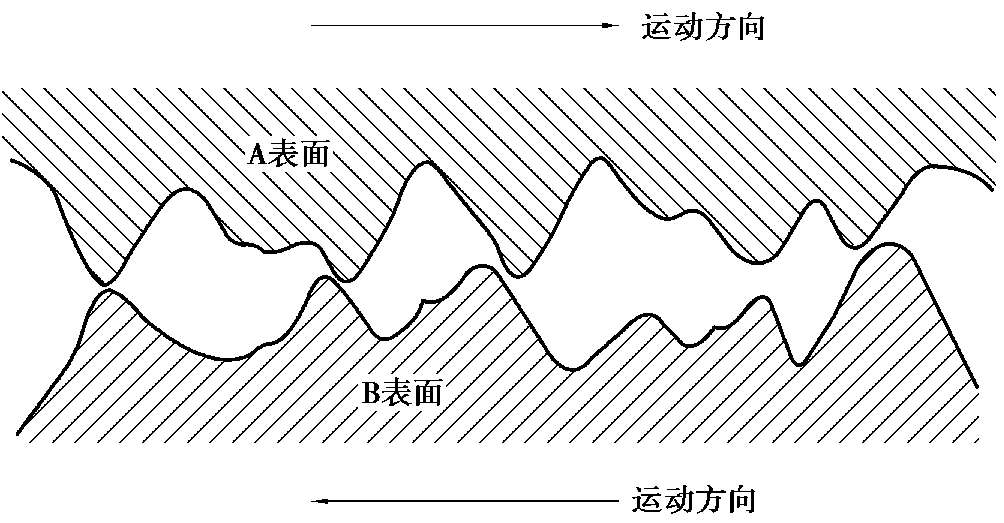
图1.9 固体真实表面接触
为了更深入地了解固体表面接触的详细信息,应着重考虑固体表面接触的实际接触面积。对接触面积,一般有 3 种定义:名义接触面积( A n )、轮廓接触面积( A c )和实际接触面积( A r )。名义接触面积又称为表观接触面积,也就是把参与接触的两表面看作理想的光滑面的宏观面积,一般情况下,它由接触表面的外部尺寸决定,是一种假设的接触面积。轮廓接触面积是指物体的接触表面被压扁部分所形成的面积,其大小与表面承受的载荷有关,仍然是一种假设的接触面积,占名义接触面积的 5%~15%。实际接触面积是指物体真实接触面积的总和,它是由粗糙表面较高微凸体接触构成的微观接触面积,其大小主要由表面粗糙度、接触物的刚性以及外界载荷的大小等因素决定。当两个固体表面接触时,实际接触面积仅为名义接触面积的一小部分,一般情况下为 0.01%~0.1%,由各个微凸体变形所形成的实际斑点直径为 3~50 pm。科学研究得到实际接触面积与载荷的关系见表 1.1,接触面积为 20 cm 2 。
表1.1 A r 与载荷之间的关系

固体表面接触一般分为单点接触和多点接触。如图 1.10 所示,当两个粗糙峰相接触时,在载荷 W 作用下产生法向变形量 δ ,使弹性球体的形状由图示的虚线变为实线。实际接触区是以 a 为半径的圆,而不是以 e 为半径的圆。由弹性力学分析得知:

于是实际接触面积 A 为:

再根据几何关系得
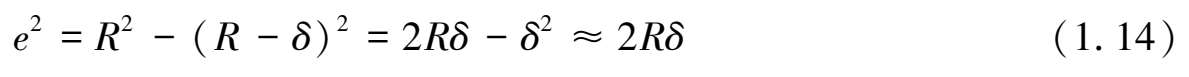
因此几何接触面积 A 0 为:

可知,单个粗糙峰在弹性接触时的实际接触面积为几何接触面积的一半。
考虑一半球形硬滑块加载在一软的光滑表面上,如图 1.11 所示。假设滑块和软表面都是绝对光滑的,也就是说,滑块和平面上没有任何微凸体。在载荷的作用下,硬质滑块和软平面之间为弹性接触,并且在软平面上方压入一个直径为 2 a 的圆形面积。赫兹于 1896 年在其经典的著作中指出:对于弹性接触来说,从压入面积的中心到任何半径距离 r 处的压缩应力 σ r ,可用式(1.16)得出:

也就是说,假如压缩应力未超过软材料的屈服应力,则最大的压缩应力位于接触面的中心,而边缘,即 r = a 时则应力降至 0,通过压痕直径的压缩应力变化如图 1.11 所示。
设所加载荷为 W ,则

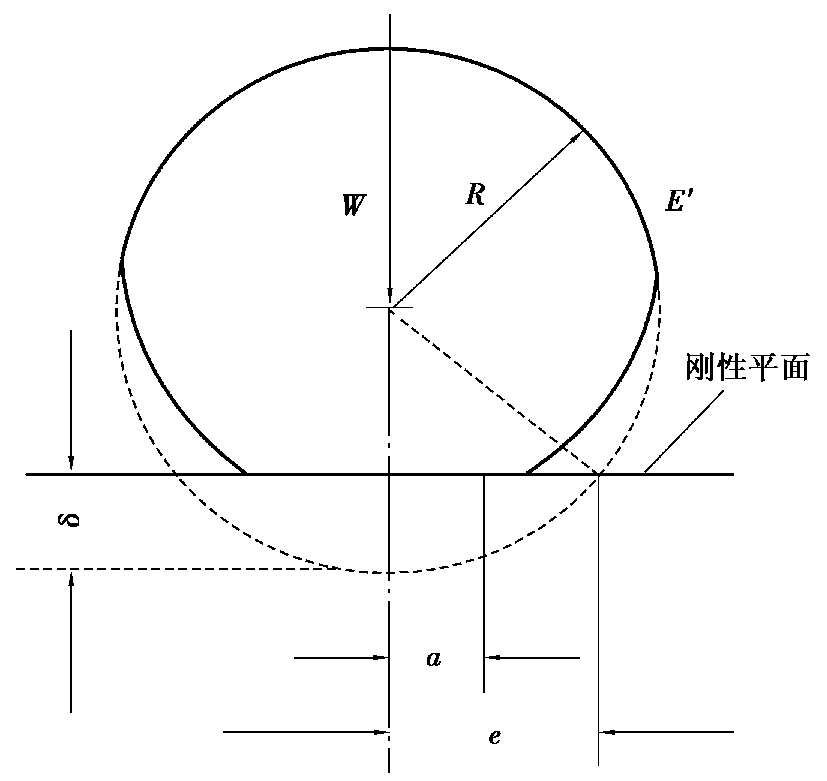
图1.10 单峰弹性接触
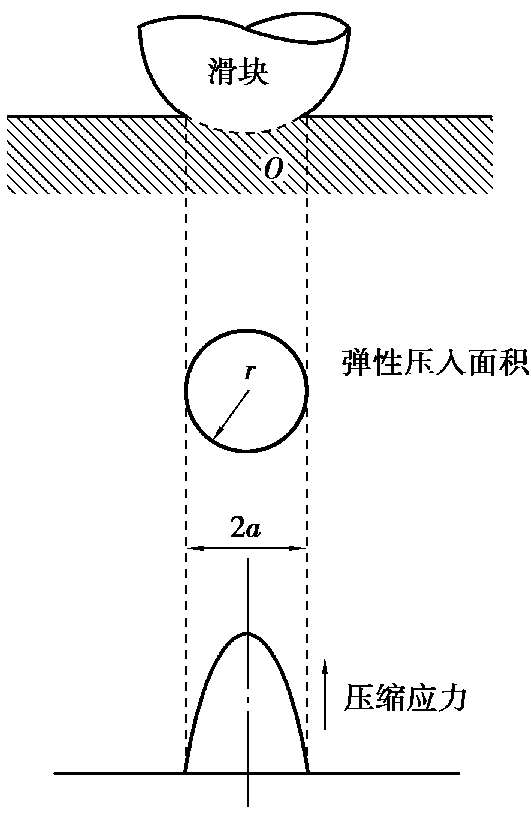
图1.11 半球形硬滑块与软光滑表面接触
赫兹的分析也证明,虽然最大法向应力是在表面上,但最大剪应力则在离表面 0.5 a 的材料内部,如图 1.11 所示的 O 处,并且有

然而,在实际的固体表面接触中往往是多点接触,像上述一半球形硬滑块与软光滑表面接触绝对不会是完全的光滑。实际上硬质滑块球上会有许多的微凸体,而这些微凸体又由许多微观的微凸体组成,并非如图 1.11 所示的那样。鉴于此,著名科学家阿查德认为,在弹性接触的情况下,实际接触面积与所加载荷的关系可用式(1.19)加以描述:

式中 m ——由固体表面接触的模型决定。
阿查德证明了若考虑微凸体的凸出部分,以后又考虑这些凸出部分本身的粗糙度。这样继续不断地分析考虑下去,如图 1.12 所示,终能到达一个阶段,此时弹性接触的面积与所加的垂直载荷非常接近于正比的关系。
粗糙峰模型除用球体外,常见的还有圆柱体模型和圆锥体模型。圆柱体模型的接触面积保持不变,这与粗糙表面的接触情况不完全一样;而圆锥体模型比较接近于实际,可用于摩擦磨损的计算。
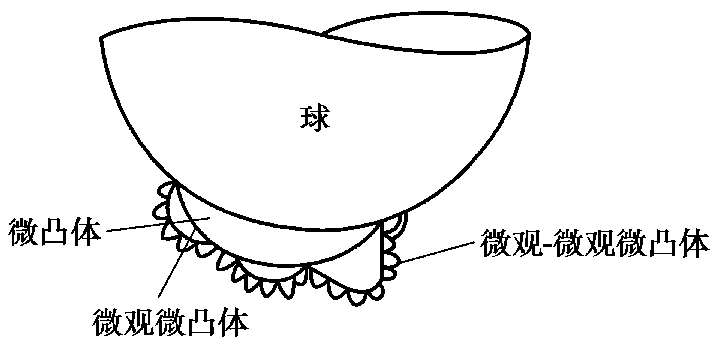
图1.12 具有微观微凸体的球