




在学习量子力学的概念时,后退一步,重新审视“经典”的概念,将它与量子计算中的表达方式联系起来,往往能帮助理解。考虑到这一点,让我们再看一看什么是“位”。
若要给我们的朋友Eve发送一条重要的信息,比如“
 ”。怎样才能以一种方便发送的方式来表示我们的信息呢?
”。怎样才能以一种方便发送的方式来表示我们的信息呢?
可以从列出每一个可以用来写出信息的字母和符号开始。幸运的是,Unicode联盟已经为我们完成了这项工作,并为世界各地用于通信的各种字符分配了代码。例如,指定I的代码为0049、
 为A66E、
为A66E、
 为2E0E、
为2E0E、
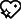 为1F496。这些代码初看似乎没有什么用,但字符与代码间的对应关系使得我们可以将符号作为信息发送。如果我们知道如何发送两种信号(称为0和1),这些代码让我们能够将更复杂的信息(比如
为1F496。这些代码初看似乎没有什么用,但字符与代码间的对应关系使得我们可以将符号作为信息发送。如果我们知道如何发送两种信号(称为0和1),这些代码让我们能够将更复杂的信息(比如
 、
、
 和
和
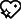 )表示为由0和1组成的信号序列。代码中的数字和字母可以逐一按以下方式表达:
)表示为由0和1组成的信号序列。代码中的数字和字母可以逐一按以下方式表达:
■ 0表示为0000; ■ 8表示为1000;
■ 1表示为0001; ■ 9表示为1001;
■ 2表示为0010; ■ A表示为1010;
■ 3表示为0011; ■ B表示为1011;
■ 4表示为0100; ■ C表示为1100;
■ 5表示为0101; ■ D表示为1101;
■ 6表示为0110; ■ E表示为1110;
■ 7表示为0111; ■ F表示为1111。
现在,我们可以发送任何我们想要的信息了,只要我们知道如何向Eve发送2个消息:“0”消息和“1”消息。利用这些对应关系,我们的信息“
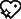 ”变成了“0001 1111 0100 1001 0110”,即1F496。
”变成了“0001 1111 0100 1001 0110”,即1F496。
提示
不要错误地发送“0001 1111 0100 1001 0100”,否则Eve会从你那里收到“
 ”!
”!
我们将每个“0”或“1”这样的信息称为一个“位”。
注意 为了将位与我们在本书其余部分看到的“量子位”区分开来,我们经常强调正在谈论的是“经典”位。
当我们使用“位”这个词时,通常是指下述两件事物之一:
■ 任何可以通过回答一个“真或假”的问题来完全描述的物理系统;
■ 存储在这种物理系统中的信息。
例如,挂锁、电灯开关、二极管、弧线球的左旋或右旋、酒杯中的酒都可以被认为是位,因为我们可以用它们来发送或记录信息(见表2.1)。
表2.1 位的示例
这些示例都应用了“位”的概念,因为我们可以通过回答一个“真或假”的问题向别人完整地描述它们。换言之,每个例子都能让我们发送一个0或1的信息。像所有的概念模型一样,位也有局限性——比如,应该如何描述桃红葡萄酒?
话虽如此,位仍然是一个有用的工具,因为我们可以描述与位互动的方式,而这些方式与我们实际构建位的方式无关。
既然我们有了一种描述和发送经典信息的方法,那么可以做什么来处理和修改它呢?我们用“操作”来描述对信息处理的方式,它被定义为描述如何改变或操纵一个模型的方式。
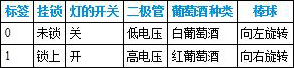
为了直观地了解NOT操作,我们假设将两个点标记为0和1,如图2.4所示。那么,NOT操作就是能够把0变成1、把1变成0的任何转换。在像硬盘这样的经典存储设备中,NOT门会翻转存储位值的磁场。如图2.5所示,我们可以认为NOT是在图2.4中画的点0和1之间实现了一个180°的旋转。
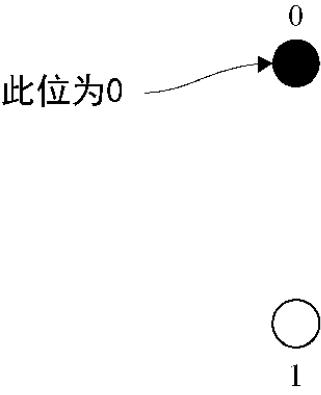
图2.4 一个经典位可以处于两种不同的状态之一,通常称为0和1。可以将一个经典位描述为处于0或1位置的黑点
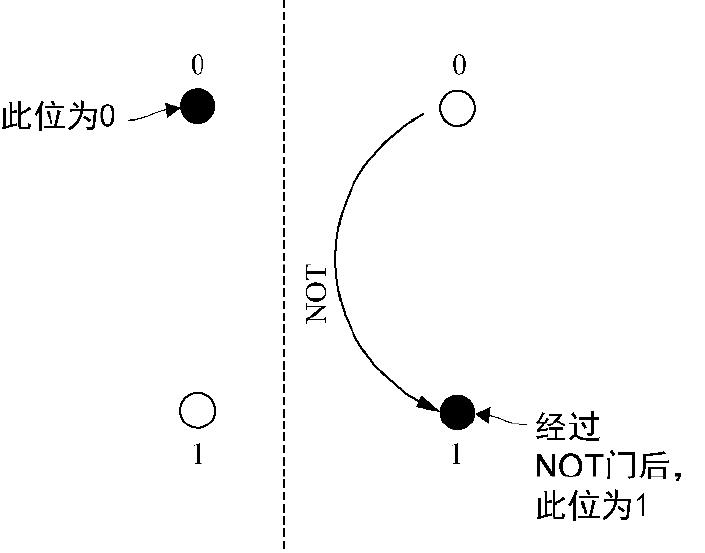
图2.5 经典的NOT操作将一个经典位在0和1之间翻转。例如,如果一个位开始是0状态,NOT将其翻转到1状态
以这种方式对经典位进行可视化,还可以让我们稍微扩展位的概念,从而包括一种描述“随机”位的方式(这在后面会有所帮助)。如果我们有一枚“公平的硬币”(也就是说,这枚硬币抛落时有一半情况下是正面,另一半情况下是反面),那么将这枚硬币称为0或1是不正确的。只有将硬币的某一面朝上放在一个平面上时,我们才知道这个位处于什么值。我们也可以抛掷它来得到一个随机值。每次抛掷硬币,我们知道它最终会落地,我们会得到正面或反面。它是正面还是反面是由一种称作硬币“偏倚”的概率所决定的。我们必须选择硬币的一面来描述偏倚,这很容易表述为一个问题,如“硬币得到正面的概率是多少?”因此,一枚公平的硬币有50%的偏倚,因为它有一半的情况下正面朝上,这在图2.6中被映射为位值0。
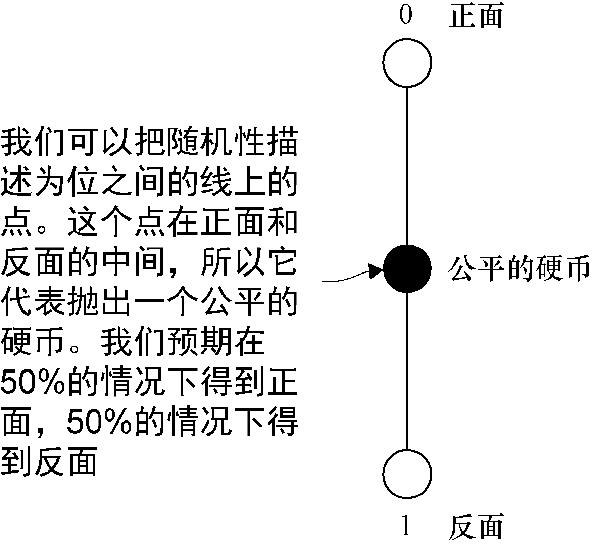
图2.6 我们可以用之前的图片来扩展位的概念,从而描述硬币。与位不同的是,硬币在每次抛出时都有概率为0或1。我们把这个概率用图形表示为0和1之间的一个点
利用这个可视化方法,我们可以把之前表示位值0和1的两个点,用一条线连接起来,然后在上面画出硬币的偏倚。我们可以更容易地看到,一个NOT操作(仍然适用于我们的新概率位)对一个公平的硬币没有任何影响。如果0和1以相同的概率出现,那么我们将0旋转到1或将1旋转到0都没有关系:我们仍然会得到0和1具有相同概率的结果。
如果我们的偏倚不在中间呢?如果我们知道有人试图通过使用动过手脚的、几乎总是落在正面的硬币来作弊,我们可以说这枚硬币的偏倚是90%,并在我们的线上画出一个点,它更接近0而不是1。
定义 我们在直线上画出每个经典位的点就是该位的“状态”。
让我们考虑一个场景。假设我想给你发送一串用挂锁存储的位。我能做到的花销最小的方法是什么?
一种方法是邮寄一个装有许多挂锁的盒子,这些挂锁要么是打开的,要么是关闭的,并希望它们以我发送时的状态到达。另一方面,我们也可以约定所有的挂锁都从0(未锁)状态开始,我可以给你发送指令,告诉你哪些挂锁需要锁上。这样,你就可以自己购买挂锁,而我只需要发送一份关于如何用经典的NOT门来准备这些挂锁的“描述”。显而易见,寄一张纸或发送一封电子邮件比邮寄一箱挂锁要便宜得多!
这展示了我们将在本书中依赖的一个原则:“一个物理系统的状态也可以用如何准备该状态的指令来描述。”因此,一个物理系统上允许的操作也定义了哪些状态是可能的。
尽管这听起来完全微不足道,但我们还可以用经典位做一件事,这对我们如何理解量子计算至关重要:我们可以观察它们。如果我观察一把挂锁并得出结论:“啊哈!那把挂锁没锁。”那么我现在可以把我的大脑看成是一个“柔软的位”。0的信息通过我的思考(“那把挂锁没锁”)而储存在我的大脑中。1的信息会通过我的思考(“啊,好吧,那把挂锁是锁着的
 ”)而储存在我的大脑中。实际上,通过观察一个经典位,我已经将它“复制”到我的大脑中。我们说,“测量”经典位的行为复制了那个位。
”)而储存在我的大脑中。实际上,通过观察一个经典位,我已经将它“复制”到我的大脑中。我们说,“测量”经典位的行为复制了那个位。
更一般地说,现代生活基于一个事实:“观察经典位而复制经典位”的过程十分容易实施。我们能够轻松地复制经典位,在我们把数据从视频游戏机复制到电视上的每一秒,都要测量数十亿个经典位。
与此不同的是,如果一个位被存储为硬币,那么测量的过程就涉及到抛掷它。测量并不完全是复制硬币,因为我在下次抛掷时可能会得到不同的测量结果。如果只有一次测量的机会,就不能断定得到正面或反面的概率。挂锁存储的位没有这种模糊性,因为我们知道挂锁的状态不是0就是1。如果我测量一个挂锁,发现它处于0状态,我就会知道它将永远处于0状态,除非我对挂锁做了什么。
在量子计算中,情况并不完全一样,正如我们在本章后面会看到的那样。虽然测量经典信息足够便宜,以至于我们会精确地抱怨一条5美元的电缆可以让我们测量多少亿位,但我们必须对如何处理量子测量更加谨慎。
无论我们如何在物理上构建一个位,都可以(幸运地)在数学和代码中以同样的方式表示它们。例如,Python提供了bool类型(以纪念逻辑学家George Boole),它有两个有效值:True和False。我们可以将位上的转换(如NOT、OR)表示为作用于bool变量的操作。重点是,我们可以通过描述一个经典操作如何转换每个可能的输入来指定该操作,这通常称为“真值表”。
定义 “真值表”是一个表格,描述了经典操作对每个可能的输入组合的输出。例如,图2.7展示了AND操作的真值表。
我们可以通过迭代True和False的各种组合,来找到Python中NAND(NOT-AND的缩写)操作的真值表,如清单2.2所示。
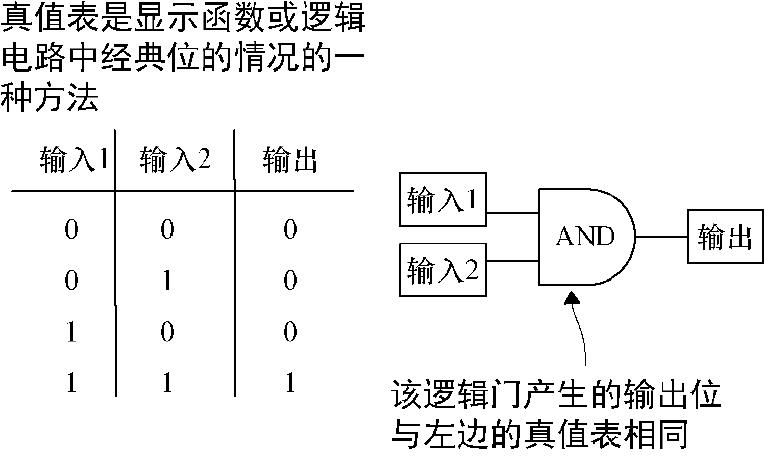
图2.7 逻辑操作AND的真值表。如果知道一个逻辑操作的整个真值表,就知道该操作对任何可能的输入分别有什么作用
>>> from itertools import product
>>> for inputs in product([False, True], repeat=2):
... output = not (inputs[0] and inputs[1])
... print(f"{inputs[0]}\t{inputs[1]}\t->\t{output}")
False False -> True
False True -> True
True False -> True
True True -> False注意 将一个操作描述为一个真值表对更复杂的操作也是适用的。原则上,即使像两个64位整数之间的加法操作也可以写成一个真值表,但这并不实际,因为两个64位输入的真值表会有2 128 个条目(数量级达到10 38 ),需要10 40 位来记录。相比之下,最近的估计认为整个互联网的大小接近10 27 位。
经典逻辑和硬件设计的大部分学问,体现在制作能够提供经典操作的紧凑电路,而不依赖潜在的大规模真值表。在量子计算中,我们对类似的量子位的真值表使用了“酉算子”(unitary operator)这个名称,我们将在接下来的讨论中展开介绍。
综上所述:
■ 经典位是可以处于两种不同“状态”之一的物理系统;
■ 经典位可以通过“操作”来处理信息;
■ “测量”一个经典位的行为使该状态中包含的信息被复制。
注意 在2.3节,我们将利用线性代数来学习量子计算机中的基本信息单位:量子位。如果你需要复习一下线性代数,这是一个跳转到附录C的好时机。我们会在全书中参考附录C中的一个比喻:我们将向量看作地图上的方向。你不妨先去看看附录C,我在这里等你!