下载掌阅APP，畅读海量书库
立即打开
在事物的发展和变化过程中，时滞通常是不可避免的，即使在以光速传递的信息系统中也不例外，又如传染病的潜伏期，弹性力学中的滞后效应等。事物的发展进程一定程度上会受时滞影响。一般情况下，时滞可使系统性能变差，甚至失稳。从研究的角度来看，时滞的存在会给系统的稳定性分析和控制器的设计等带来很大的困难。对于微分方程来说，时滞的存在影响着方程解的性质。一般时滞微分方程用于描述依赖当前和过去历史状态的动力学系统，在物理、工程、信息、经济、化学以及生物数学等领域都有着非常重要的作用。因此，这使得人们对时滞微分系统产生了浓厚的研究兴趣，并得到了丰硕的研究成果。
俄国数学力学家Lyapunov对时滞微分方程的稳定性理论的研究做出了突出贡献，1892年，Lyapunov的博士论文《运动稳定的一般问题》给出了研究稳定性的一种非常有效的方法，被后人称为Lyapunov直接方法，亦称为Lyapunov第二方法，从而建立了稳定性理论研究的框架。目前它仍是研究时滞微分方程稳定性的主要方法。这种方法的优点是可以在没有得到方程具体解的情况下，就可以确定方程解的稳定性。随着时间的推移，特别是大系统理论、自动控制、空间技术和生物数学等的出现，使得稳定性理论飞速发展，众多学者为稳定性理论的研究奠定了坚实的基础，使其形成了一套比较完善的理论。
时滞系统不能用微分方程来描述，而是需要用微分差分方程，也称为时滞微分方程，或具有偏差变元的微分方程。下面给出时滞微分方程的稳定性定义及稳定性理论。
一般形式的滞后型微分差分方程 [86-88] 形如
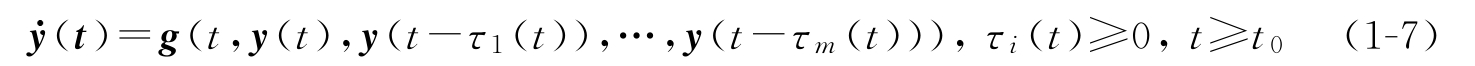
系统（1-7）的初始条件为
y （ t ）= φ （ t ）， t ∈[ t 0 -τ ， t 0 ]
其中，
，
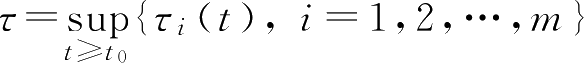φ
（
t
）足够光滑，保证柯西问题解存在唯一性。
设 y * 是系统（1-7）的平衡点，做平移变换 x （ t ）= y （ t ） -y * ，则式（1-7）改写为
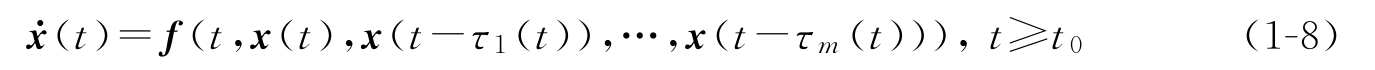
相应地系统（1-8）的初始条件为
x （ t ）= ξ （ t ）， t ∈[ t 0 -τ ， t 0 ]
其中， ξ （ t ）= φ （ t ） -y * 。
要证系统（1-7）的平衡点 y * 的稳定性，可通过就证明系统（1-8）的零解 x = 0 的稳定性来确定。下面给出相关的稳定性的定义，这些定义引自文献［88］。
定义1-2
称系统（1-8）的零解稳定，若对任意
ε
＞0，
t
0
∈
I
，存在
δ
（
ε
，
t
0
）＞0，使得对任意
ξ
（
t
），
t
∈[
t
0
-τ
，
t
0
]，当
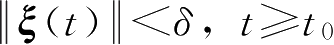时，有
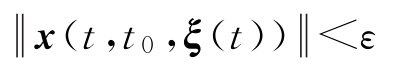
定义1-3
称系统（1-8）的零解是吸引的（一致吸引的），若存在
σ
（
t
0
）>0（
σ
＞0），对任意
η
＞0，存在
T
（
t
0
，
η
）
＞0（
T
（
η
）
＞0），使得当
，
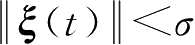t
≥
t
0
+
T
时，有
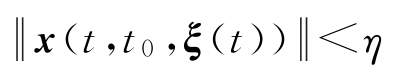
定义1-4
称系统（1-8）的零解一致稳定，若对任意
ε
＞0，
t
0
∈
I
，存在
δ
（
ε
）＞0，使得对任意
ξ
（
t
），
t
∈[
t
0
-τ
，
t
0
]，当
，
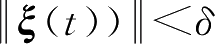t
≥
t
0
时，有
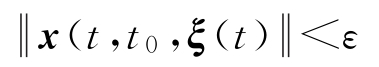
定义1-5
称系统（1-8）的零解渐近稳定，若系统（1-8）的零解是稳定的，且存在
δ
（
t
0
）＞0，对任意
ξ
（
t
），
t
∈[
t
0
-τ
，
t
0
]，当
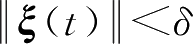时，有
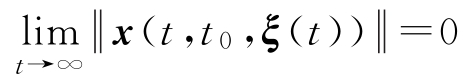
定义1-6
称系统（1-8）的零解一致渐近稳定，若它一致稳定，且存在
σ
>0（
σ
不依赖于
t
1
，
t
1
>
t
0
），对于任意
ε
>0，存在
T
（
ε
）>0（不依赖于
t
1
），当
t
>
t
1
+
T
（
ε
），
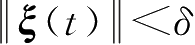时，有
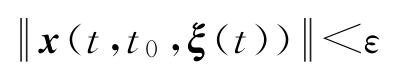
如果系统（1-8）的零解为稳定的和吸引的，则它是渐近稳定的；如果系统（1-8）的零解为一致稳定的和一致吸引的，则它是一致渐近稳定的。
定义1-7 称系统（1-8）的零解为全局渐近稳定，若它是稳定的，且对任意初始函数 ξ （ t ），有
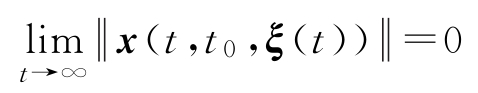
定义1-8
称系统（1-8）的零解指数稳定，若对任意
ε
>0，存在正数
λ
>0和
δ
（
ε
）＞0，使得当
时，对于
t
≥
t
0
，
t
0
∈
I
，有
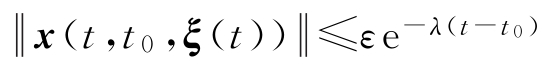
定义1-9
称系统（1-8）的零解全局指数稳定，若对任意
σ
>0，
λ
>0，
M
≥1，使得当
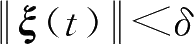时，对于
t
≥
t
0
，
t
0
∈
I
，有
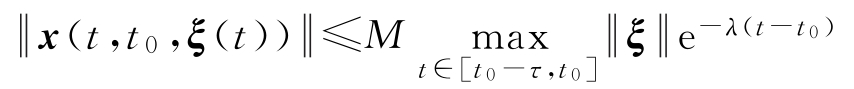
定义1-10
[89]
称系统（1-8）的零解多项式稳定，若对任意
ε
>0，存在
λ
>0和
δ
（
ε
）＞0，使得当
时，对于
t
≥
t
0
，
t
0
∈
I
，有
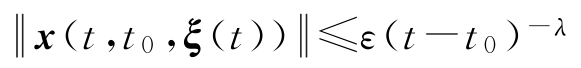
定义1-11
[89]
称系统（1-8）的零解全局多项式稳定，若对任意
σ
>0，存在
λ
＞0，
M
≥1，使得当
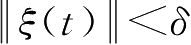时，对于
t
≥
t
0
，
t
0
∈
I
，有
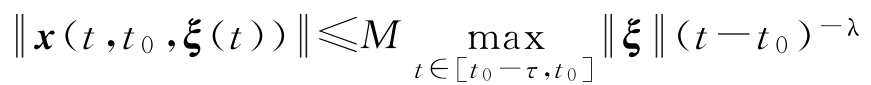
设 Ω 是包含原点的 n 维开邻域，令 I =[0，+∞），函数 W （ x ）∈ C （ Ω ，ℝ）， V （ x ， t ）∈ C （ Ω ，ℝ）。下面给出函数正定（负定），半正定（半负定）及Lyapunov函数等的定义 [9，89] 。
定义1-12 称函数 W （ x ）在 Ω 上正定（负定），若 W （ x ）≥0（ -W （ x ）≥0），且当且仅当 x = 0 时， W （ x ）=0。
正定和负定的函数 W （ x ）都称为Lyapunov函数。
定义1-13 称 W （ x ）在 Ω 上半正定（半负定），若 W （ x ）≥0（ -W （ x ）≥0），且 W （ x ）=0有非零解。
定义1-14
称
W
（
x
）是无穷大正定函数，若对于正定函数
W
（
x
）∈
C
（ℝ
n
，ℝ），当
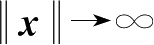时，
W
（
x
）→∞有非零解。
定义1-15 称函数 V （ x ， t ）在 Ω × I 上正定（负定），若存在正定函数 W （ x ），使得 V （ x ， t ）≥ W （ x ）（ -V （ x ， t ）≥ W （ x ）），且 V （ 0 ， t ）≡0。
为了方便，考虑系统（1-8）的简洁系统（含有一项时滞项）
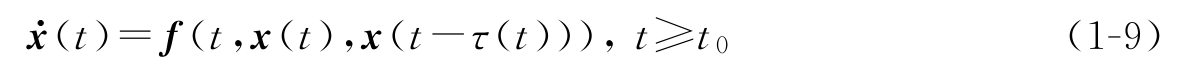
其中 x ∈ℝ n ， f ∈ C [ I ×ℝ n ×ℝ n ，ℝ n ]， f （ t ， 0 ， 0 ）≡ 0 ，0≤ τ （ t ）＜∞。
定义1-16 称 V （ x ， t ）∈ C （ Ω × I ，ℝ）在 Ω × I 上有无穷小上界，若存在正定函数 W 1 （ x ）∈ C （ℝ n ，ℝ），使得
| V （ x ， t ）|≤ W 1 （ x （ t ））
称 V （ x ， t ）在 Ω × I 上有无穷大下界，若存在无穷大正定函数 W 2 （ x ），使得
V （ x ， t ）≥ W 2 （ x ）
定理1-1
若在某区域
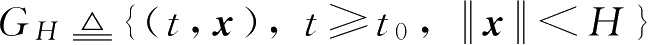上，存在正定函数
V
（
x
，
t
），且
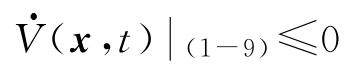
特别的，
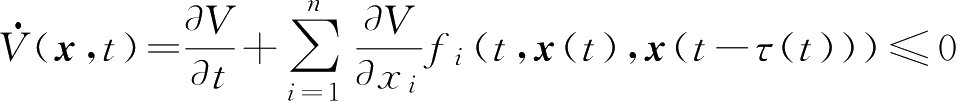，则系统（1-9）零解稳定。
定理1-2 若在某区域 G H 上，存在具有无穷小上界的正定函数 V （ x ， t ），且
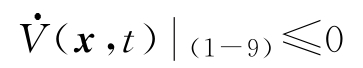
特别的，
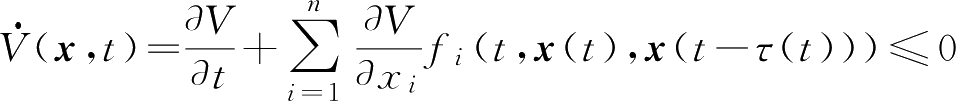，则系统（1-9）零解一致稳定。
定理1-3 在某区域 G H 上，若存在具有无穷小上界的正定函数 V （ x ， t ），且
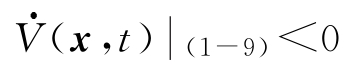
特别的，
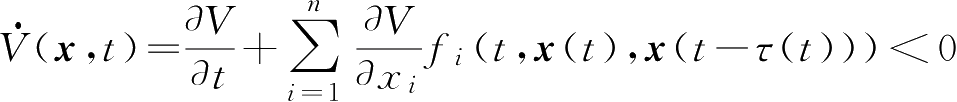，则系统（1-9）零解一致渐近稳定。
定理1-4 在某区域 G H 上，若具有无穷小上界的无穷大正定函数 V （ x ， t ），且
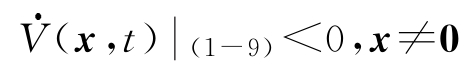
成立，则该系统（1-9）的零解全局一致渐近稳定。