根据数据传递类型,流固耦合问题可分为单向流固耦合分析(uni-direc-tional coupling)和双向流固耦合分析(bi-directional coupling)。其中,双向流固耦合分析又可分为顺序求解法和同时求解法。基于流体诱导振动强化换热问题,采用双向流固耦合的顺序求解法数值计算弹性管束在壳程和/或管程流体诱导下的振动响应,分别利用Transient Structural(瞬态动力学)模块和CFX模块开展弹性管束瞬态动力学分析和管壳程流场计算。
1.流体诱导振动计算流程
图2-2所示为利用ANSYS CFX和ANSYS计算壳程流体诱导弹性管束振动强化换热的计算流程图。将壳程流体域和管束结构域网格相应导入ANSYS CFX和ANSYS中,并进行边界条件和双向流固耦合计算初始化设置,考虑弹性管束振动引起的湍流,选用标准的 k-ε 湍流模型 [3] ,设置流固耦合计算的时间步 t 和总时间 T 。设置交错迭代最大次数 i max =10,表示在一个流固耦合时间步 t 内进行最多10次的迭代计算,通常不到10次迭代计算就可使耦合时间步达到收敛。
第一步:计算壳程对流换热。根据弹性管束结构域传递到壳程流体域的位移信息更新壳程流体域网格边界,该问题属于流致振动计算,因此第一步计算时位移信息为0。利用ANSYS CFX求解壳程流体域的控制方程,获得该时刻壳程内的流体速度、温度及压力等信息,压力数据通过流固耦合面传递到弹性管束结构域。
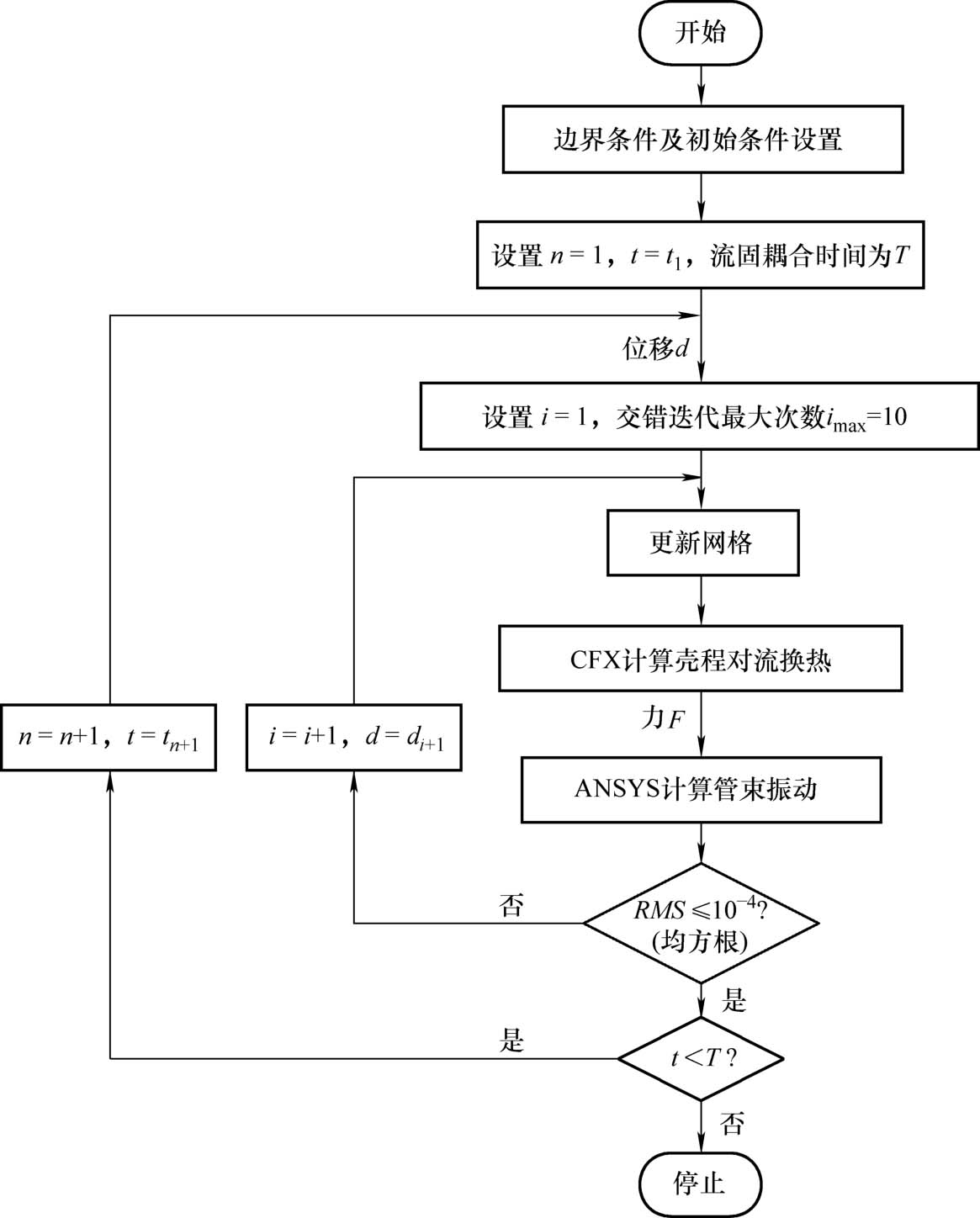
图2-2 流体诱导弹性管束振动强化换热的计算流程图
第二步:计算弹性管束振动响应。在弹性管束结构域中,通过流固耦合面获得第一步计算得到的流体压力信息,将流体压力作为管束边界条件施加到弹性管束管壁上,利用ANSYS求解该流体作用力下的管束运动方程,计算得到相应的管束振动响应。各变量依据 RMS 是否小于等于10 -4 判断在该流固耦合时间步下是否实现收敛,如果没有收敛,则将得到的管束振动位移通过流固耦合面传递到壳程流体域,结合动网格技术更新壳程流体域网格 [4] ,继续迭代计算,直到该流固耦合时间步实现收敛。
第三步:下一流固耦合时间步计算。当前一个时间步内实现收敛后,将进行下一耦合时间步的计算,将上一耦合时间步得到的管束位移信息通过流固耦合面传递到壳程流体域,计算方法同上,依次计算壳程对流换热和管束振动响应,直到完成流固耦合总时间 T 的计算,则壳程流体诱导弹性管束振动强化换热数值计算完成。
其中,基于扩散光顺方法更新网格,网格运动的扩散方程为 [5]

式中, u mf 为网格移动速度,单位为m/s; γ 为扩散系数。
扩散系数 γ 为网格体积 V 的函数
γ =1 /Vα
式中, α 为控制参数,通过控制网格边界运动来影响内部网格的运动。
利用有限体积法迭代计算式(2-14),节点位置更新方程为

2.流体诱导振动计算数值验证
在进行壳程流体诱导振动强化换热分析之前,首先要验证该数值计算方法的准确性,包括壳程内的对流换热以及弹性管束的振动响应计算。对文献[6]中盘管式换热器壳程对流换热进行数值计算结果验证,盘管式管束与平面弹性管束结构类似,且已明确给出固定螺旋管束的换热经验关系式为
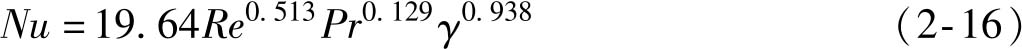
式中, Pr 为普朗特数; γ 为节距。
采用本文的数值计算方法分析盘管式换热器壳程对流换热,边界条件与文献[6]中的工况一致,图2-3所示为壳程对流换热的数值结果与关系式结果的对比验证。图中所示数值结果与关系式计算结果吻合良好,平均误差在1.58%以内,最大误差为2.87%,表明该数值计算方法和湍流模型的选取准确。
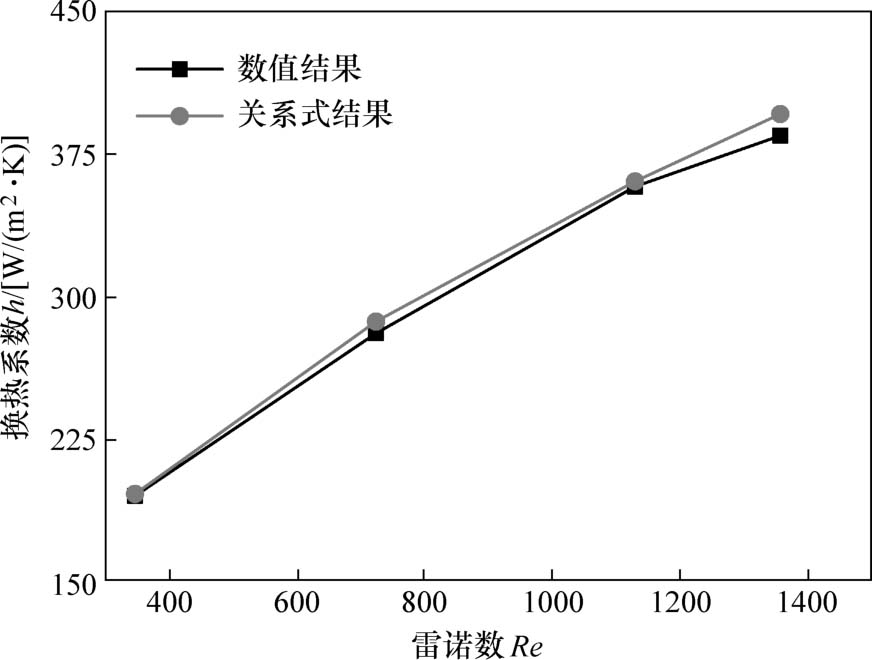
图2-3 壳程对流换热的数值结果与关系式结果的对比验证
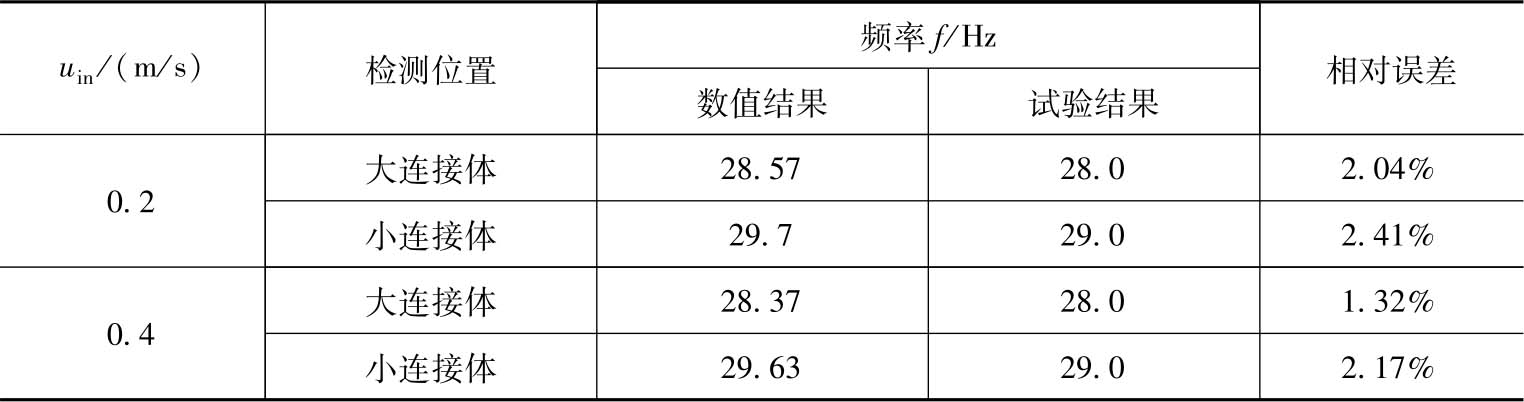
对于流体诱导弹性管束振动计算,以单排弹性管束流体诱导振动试验为参照,建立与试验一致的几何模型进行流体诱导弹性管束振动数值计算,数值结果与试验结果的对比见表2-1。从表中可知,数值结果与试验结果具有较好的一致性。当入口速度为0.2m/s时,小连接体的振动主频最大误差为2.41%;入口速度为0.4m/s时,大连接体的振动主频最大误差为1.32%。对比结果表明,本文采用的双向流固耦合计算方法求解壳程流体诱导弹性管束振动强化换热是可行的,数值计算结果较合理,验证了该数值计算方法的准确性。
表2-1 数值结果与试验结果的对比