




由于管束的锥形螺旋结构,管束Ⅰ、Ⅱ通过连接体M相互影响,不能简单等效为两端简支曲梁结构或壳结构进行计算。依据动态子结构原理,将管束Ⅰ、Ⅱ及连接体M处理为子结构(见图1-18)。依据固定界面模态综合法原理,管束Ⅰ、Ⅱ及连接体M界面处的位移矢量为 q 1 、 q 2 ,相应的界面力为 F 1 、 F 2 。对于管束的三维振动,每个位移矢量包含三个平动分量和三个转动分量,即 q i =( u i v i w i θ xi θ yi θ zi ) T , i =1,2。
利用超单元法求解单根螺旋管束的质量矩阵 m 和刚度矩阵 k ,通过静力方程求解其主模态和约束模态,利用主模态和约束模态组成变换矩阵,完成一次坐标变化,将管束的物理坐标转换为模态坐标,得到管束在模态坐标下的振动方程
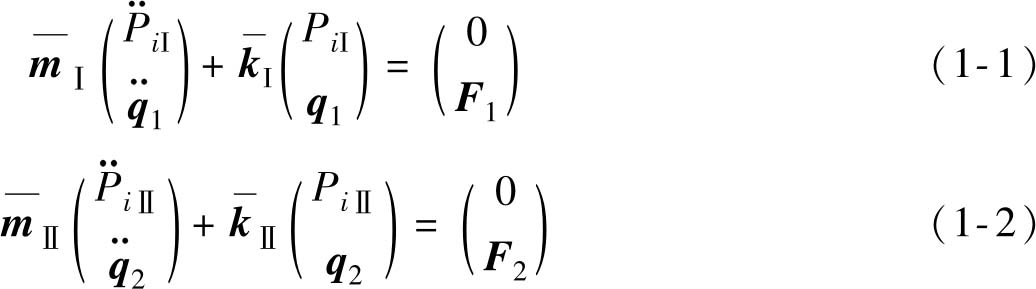
式中,
P
i
为子结构的模态坐标;
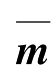 为子结构模态坐标下的质量矩阵;
为子结构模态坐标下的质量矩阵;
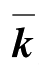 为子结构模态坐标下的刚度矩阵。
为子结构模态坐标下的刚度矩阵。
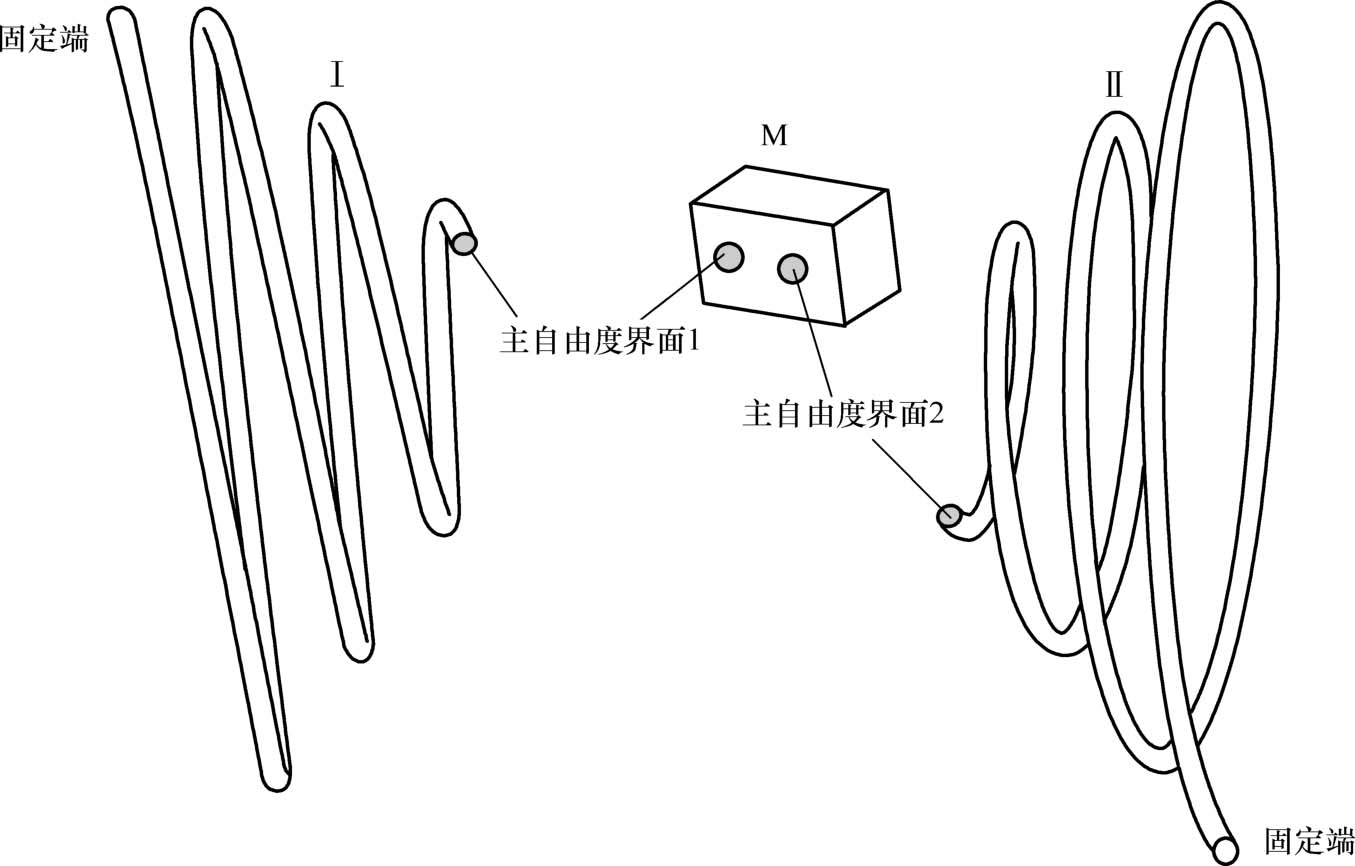
图1-18 管束子结构的模型
矩阵中的元素由子结构在固定界面条件下的模态信息确定。对于刚性连接体M,其振动方程为

联立式(1-1)~式(1-3),可得

式中,
F
为子结构的界面力矢量;
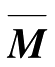 为子结构质量矩阵组成的对角矩阵;
为子结构质量矩阵组成的对角矩阵;
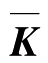 为子结构刚度矩阵组成的对角矩阵。
为子结构刚度矩阵组成的对角矩阵。
广义模态坐标矢量 P 和界面力矢量 F 表示为
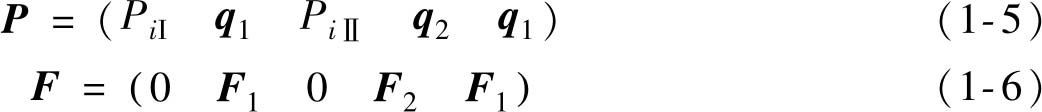
由此可知模态坐标矢量 P 中存在不独立的广义坐标,根据界面位移连续条件,取独立的广义坐标矢量

进行第二次坐标变换

式中, Q 为变换矩阵。
由此得到锥螺旋管束在模态坐标下的无阻尼振动方程

式中, M 为管束总体质量矩阵; K 为管束总体刚度矩阵。
利用数值方法求解方程,然后经过两次返回坐标变换,得到锥螺旋管束的频率和振型。