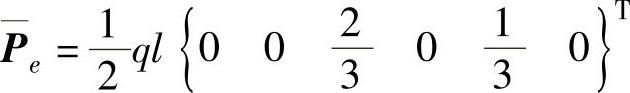通过外力势能研究外力对单元的作用效果,将单元内分布载荷转化为等价作用效应的等效节点载荷。
所谓体力是指分布在物体内部的力,如重力、离心力、惯性力等。对于平面问题,体力有两个分量 p ={ X Y } T ,单元体力势能是在单元区域内积分,即
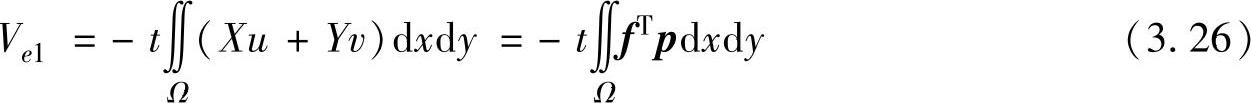
所谓面力是指作用在物体表面上的力,内部单元边界之间的相互作用属于内力,不属于面力范畴,只有边界单元才可能存在面力作用。面力有两个分量
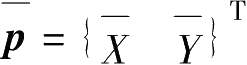 ,单元的面力势能只能在有面力作用的边界上进行积分,即
,单元的面力势能只能在有面力作用的边界上进行积分,即
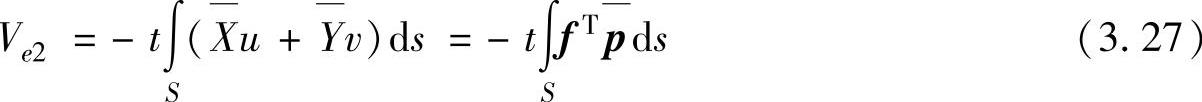
积分域为有面力作用的边界,对于平面问题是曲线,三维问题则是曲面。
建立有限元模型时,通常将集中力作用点设置为节点,因此集中力的势能不用积分。设单元节点作用的集中力为 P 0 e ,则其单元的外力势能为

单元总的外力势能是单元上各种外力势能之和,为

说明一点,当集中力作用在单元的节点上时,集中力作用点的周围往往有多个单元,多个单元拥有共同节点,因为有限元分析最终考虑的是所有单元势能之和,不必考虑集中力在单元之间的分配问题,直接将该节点集中力叠加到总的载荷矢量中,因此在计算单元外力势能时,一般不包含集中力势能 V e 3 。
将位移模式 f = Nδ e 代入式(3.26)中,并考虑单元节点位移矢量 δ e 是不变量,单元的体力势能表达为
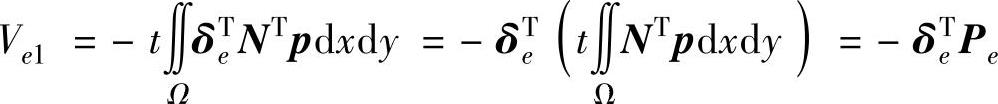
式中,

P e 称为体力的等效节点载荷矢量。将三角形单元的形函数矩阵即式(3.7)代入,式(3.30)更形象具体,表示为
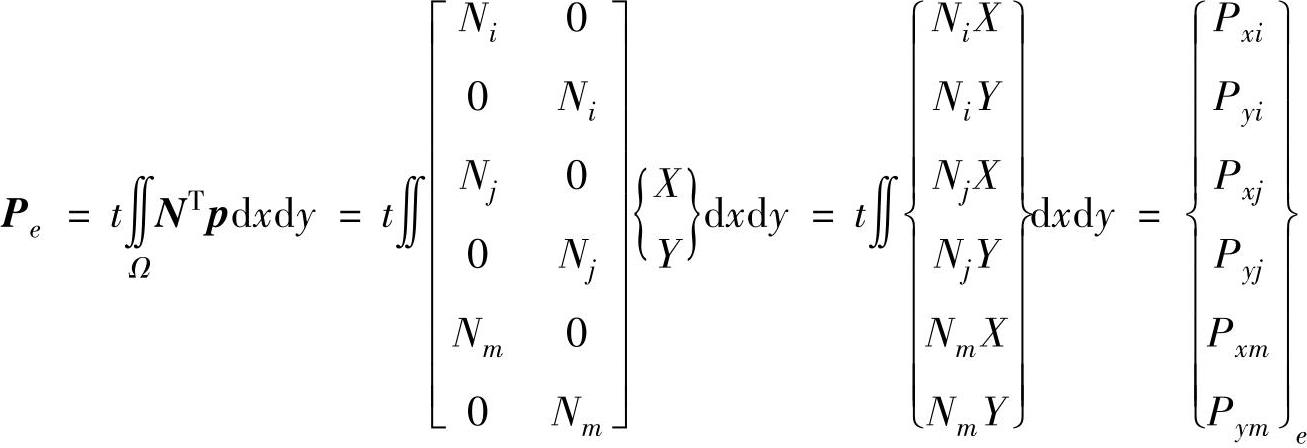
综上可见,在计算体力势能时,由于采用位移模式来表达单元内的位移场,使得原本在单元内部连续分布的体力,变为单元节点的集中载荷,外力的作用点发生了变化,称为载荷移置。依据静力等效原则,对于给定的位移模式,载荷移置的结果是唯一的,转化的节点载荷称为等效节点载荷或等效节点力。
通常单元划分得比较细小,体力变化不太大,可认为体力在单元内为常量,即单元内的体力分量 X 、 Y 为常量,等效节点载荷矢量 P e 中的某个元素为
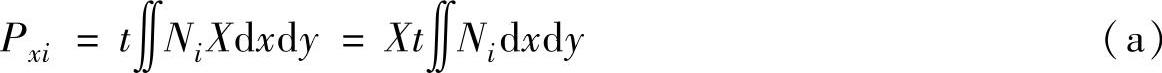
积分项
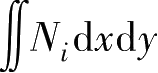 的计算,有两种计算方法:
的计算,有两种计算方法:
其一,将形函数的表达式(3.4)代入,得
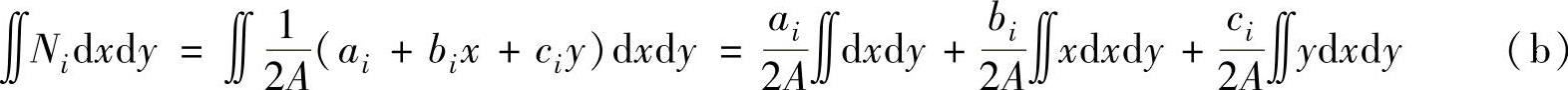
根据力学物理意义,
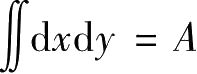 表示积分域的面积;
表示积分域的面积;
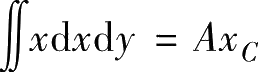 和
和
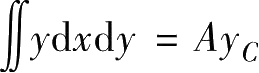 则表示面积矩。所以,式(b)
则表示面积矩。所以,式(b)
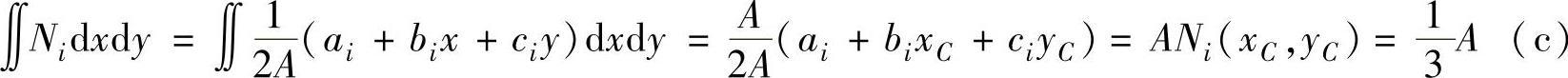
其二,利用面积坐标积分公式(3.10)直接计算。式(a)中,只有 N i 这一项,即 α =1、 β = γ =0,则
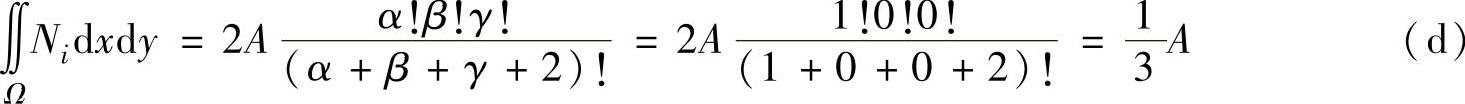
两种方法计算结果相同。所以,式(a)为

对于 y 方向和其他节点的等效载荷与此处理方式类似。当体力为常量时,单元等效节点载荷统一写成矩阵形式
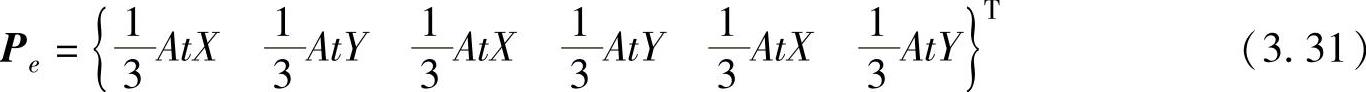
式中, At 是单元体积; AtX 、 AtY 实际是单元体力在 x 和 y 方向上的合力。当体力为常量时,先计算出单元体力的合力,然后再平均分配到对应的3个节点上,即可得到体力的等效节点载荷。
根据面力势能的表达式(3.27)及位移模式的表达式(3.8),单元的面力势能表达为
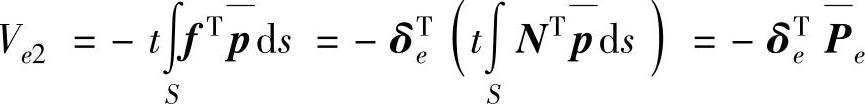
需要说明的是,内部单元之间相互作用的表面力互为作用与反作用力,在整体分析时内部节点面力互相抵消,不必考虑内部单元之间的表面力。只有边界单元中处于边界位置且有面力作用的边,才需要计算该边上的面力等效节点载荷。
单元内节点的面力等效节点载荷为“0”,如果在 ij 边上存在面力,此时 N m =0,则面力等效节点载荷矢量为
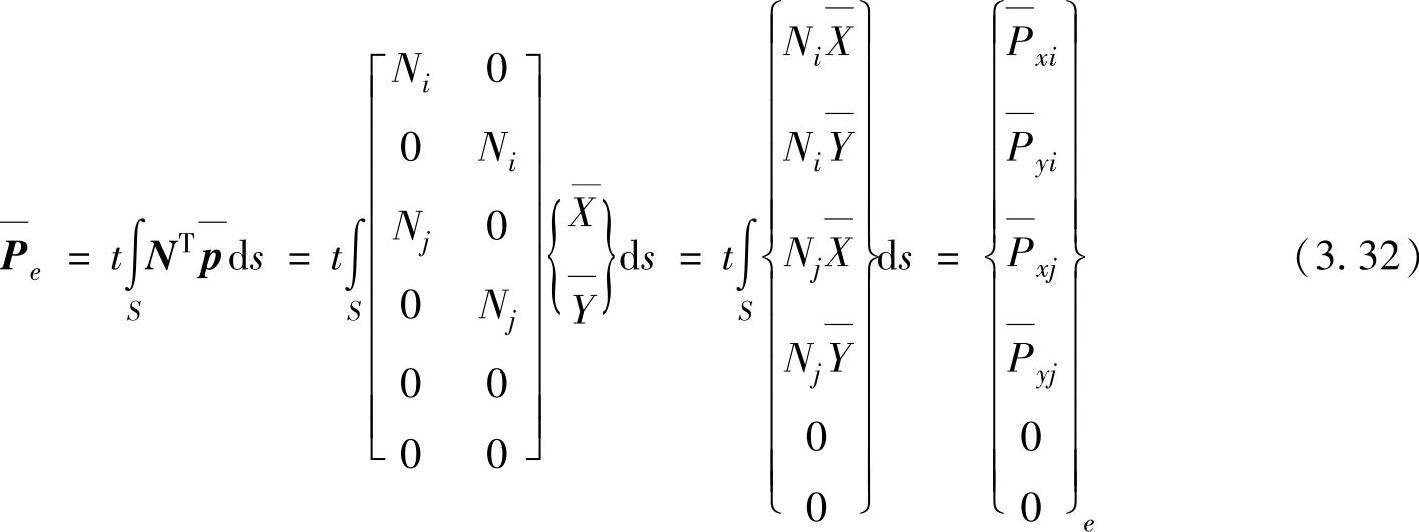
物体表面力作用方向及大小分布有不同的形式,如面力作用方向有法线方向、切向方向或倾斜方向,面力大小则有线性或高次分布方式。下面以线性分布面载荷为例,讨论图3.5所示的常见三种形式面力等效节点载荷的计算。
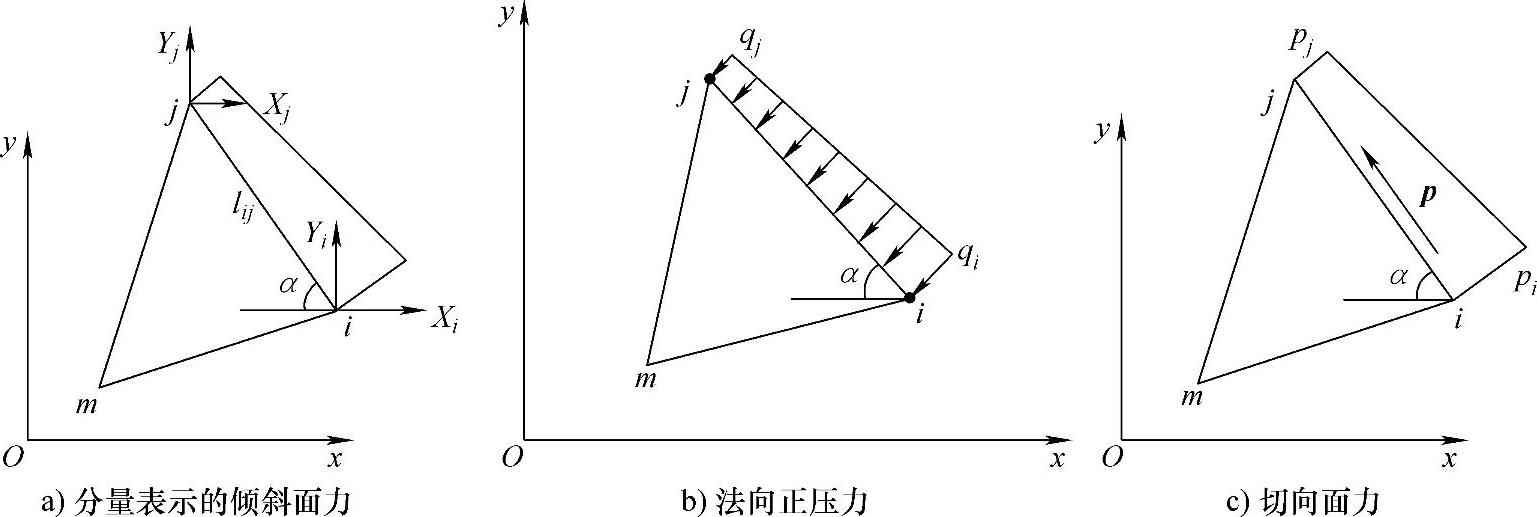
图3.5 线性分布的面力形式
如图3.5a所示,在
ij
边上线性分布面力,两个节点的面力分量分别为
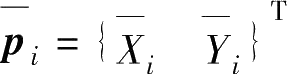 和
和
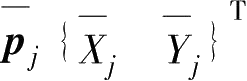 。根据
i
、
j
节点的值确定,
ij
边上任意
Q
点处面力的大小,符号按其与坐标轴的方向确定,面力分量为
。根据
i
、
j
节点的值确定,
ij
边上任意
Q
点处面力的大小,符号按其与坐标轴的方向确定,面力分量为

将上式代入式(3.32),利用面积坐标积分公式(3.11),得到以坐标分量表示的、线性分布面力作用下,单元的等效节点载荷为
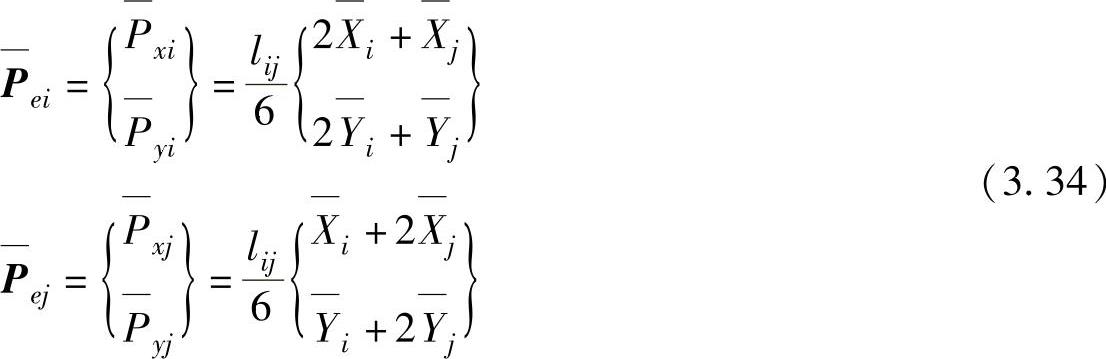
式中, l ij 表示单元 ij 边的长度。
表面力垂直于物体表面且按线性分布的压力是最常见的表面力形式,如水坝迎水面的水压力就是与水深成正比且垂直于迎水面。若某单元 ij 边上有线性分布的法向面力,单元在 ij 边左侧,节点 i 的值为 q i ,节点 j 的值为 q j ,规定指向物体(压力)为正,背离物体(拉力)为负,如图3.5b所示。
法向面力 q ,在两个坐标轴上投影的面力分量为
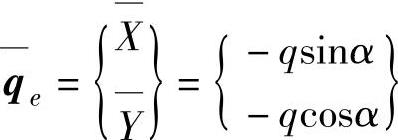
其中,
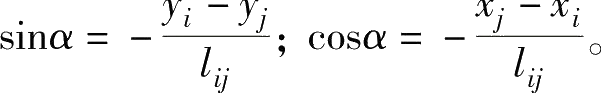
将法向面力 q 在坐标轴上的面力分量代入式(3.33),则线性分布的法向面力在 ij 边上任意一点的面力分量为
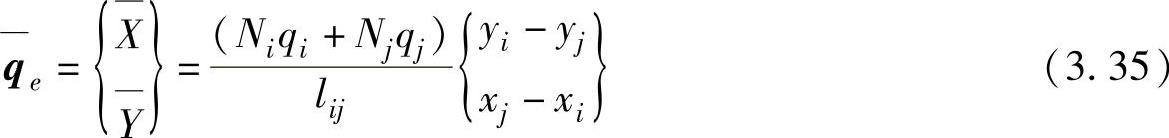
按计算式(3.34)时用到的类似的积分方法,线性分布的法向面力作用在 i 、 j 节点的等效节点载荷分别为
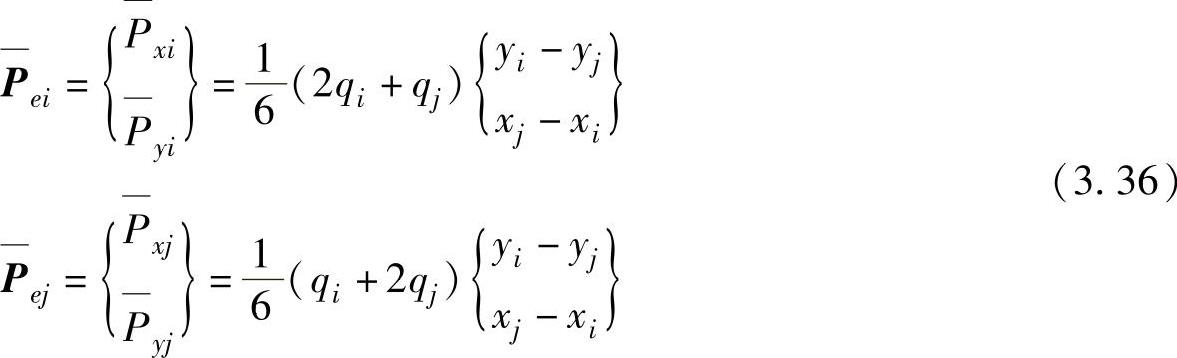
摩擦力属于边界面内的表面力,其方向与边界切线方向平行。切向面力符号规定:沿着切向面力箭头指向,单元在前进方向的左侧为正,反之为负,如图3.5c所示。
若某单元边界上存在线性分布的切向面力 p ,切向面力在 ij 边上任意一点的面力分量为
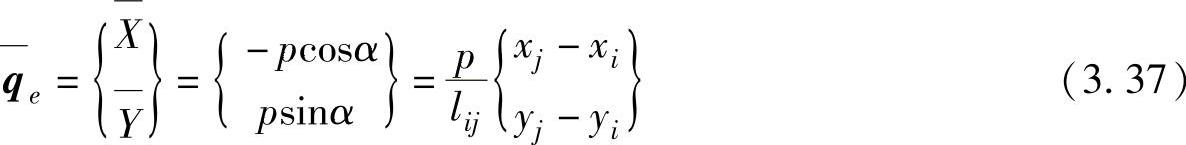
按上述步骤,线性分布的切向面力的等效节点载荷为
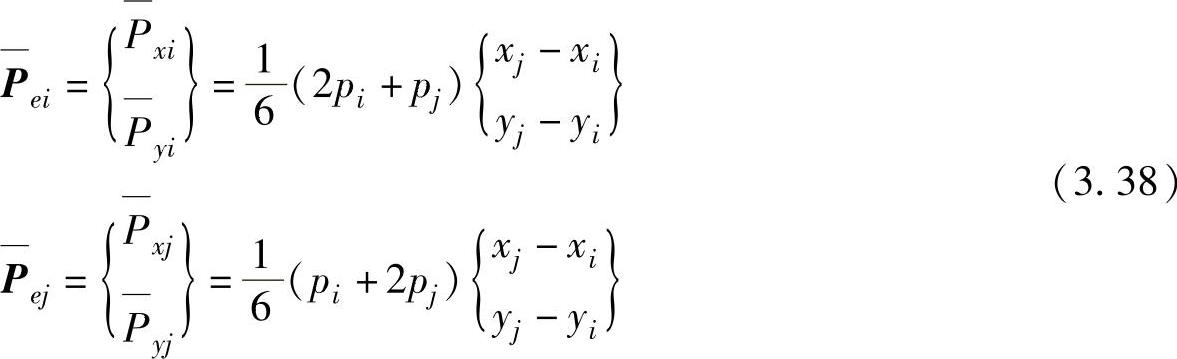
切向面力为常量时,式(3.38)简化为均布切向面力作用下的等效节点载荷为
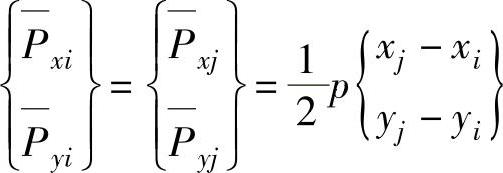
【例3.1】 如图3.6所示,单元在 jm 边上有 x 方向的面力作用,设该边长度为 l ,单位厚度,求该单元的等效节点载荷。
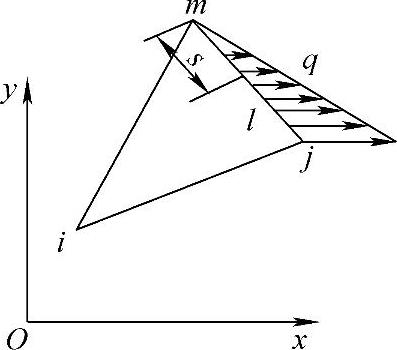
图3.6 线性分布面力
解法一 :设以 m 点为原点,沿 jm 边上任意位置 s (0≤ s ≤ l )处的面力分量为
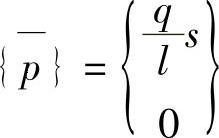
形函数的值为
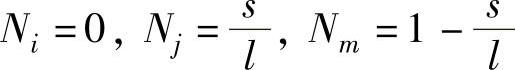
根据面力的等效节点载荷,即式(3.32),只有
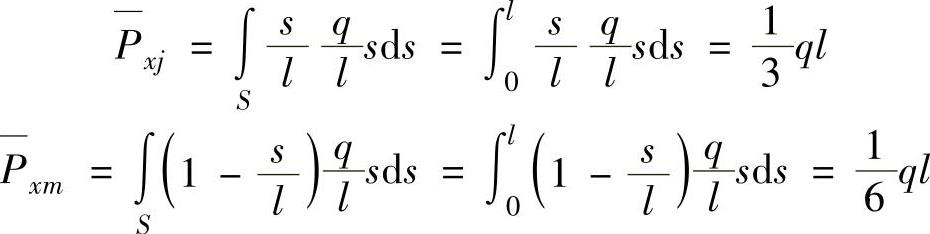
其余各个分量均为零。单元的面力等效节点载荷为
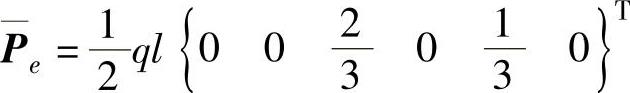
实际上, ql/ 2为面力在边界上的合力。当面力不是均布力时,面力的等效节点载荷不再是平均分布,但也可先计算出面力的合力,然后根据合力作用点的位置按比例分配到相应节点上。
解法二 :根据形函数的性质,在 jm 边上任意位置 s 处的面力分量,可以表示为
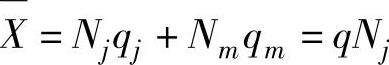
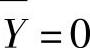
根据面积坐标积分公式(3.11),得到
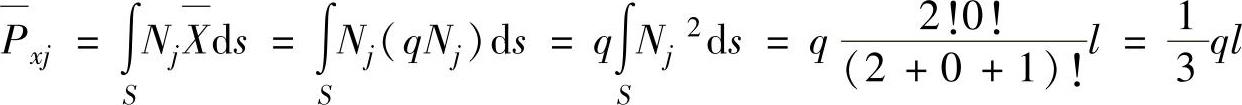
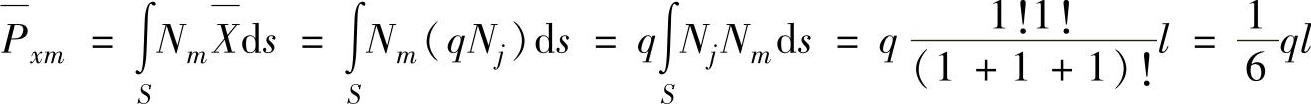
其余各个分量均为0。面力的等效节点载荷为