




有限元法的第一步是用假想的线或面将原连续的弹性体或结构划分成足够多、有限数目的形状简单的小区块,即单元,单元通过节点相连,这种通过单元集合体来描述被求解原始弹性体的过程称为建立有限元模型。有限元模型是对结构实体的全面数字化描述,不仅包括原始结构或称实体模型划分的有限元单元网格,同时还包含载荷作用和边界条件等多种类型数据。建立合理的有限元模型是有限元分析的基础,直接影响有限元计算精度甚至决定计算成败的关键。建立有限元模型,首先应做到:
(1)选择合理的单元类型 选择的单元必须能够反映出弹性体或结构的几何特征。满足几何特征的单元不止一种,可参考第1章表1.1中所列出的单元应用范围,并综合考虑计算工作量和计算精度要求等多种因素选择单元类型。
(2)确定适当的求解区域 为减少计算的工作量,要充分考虑和利用弹性体或结构几何形状及作用载荷的对称性,确定弹性体或结构的求解区域,即划分网格的范围。
(3)建立统一的坐标系 有限元分析需要将计算模型数字化,必须在统一的坐标系下描述各类数据。原则上坐标系的选取是任意的,但为方便起见,坐标轴尽量与分析结构的边界线平行。若利用了结构的对称性,建议将坐标轴设在对称面上。
单元的形状多样,单元的尺寸大小与数量没有限制,因此有限元模型具有多样性,但结构离散化必须遵循一定的原则。为了合理地划分单元网格,下面以平面三角形单元为例,阐述在结构离散化时应注意的问题:
(1)共边性要求 单元必须覆盖被分析结构或弹性体的整个区域,单元之间既不允许相互重叠,也不允许相互脱离,保证相邻单元共边,以保证用单元集合表示的离散体几何形状与原结构的相似性。
(2)共点性要求 有限元模型是通过节点相互联系的,要求任意三角形的顶点必须是相邻单元的顶点,不许落在其他单元内部或边线上,否则计算过程中会出现错误,图3.1a是错误网格,图3.1b是正确网格。
(3)单元的边长应尽可能接近 采用规则的锐角三角形单元可提高计算精度,同一单元中最长边与最短边之比不宜大于2,相邻单元尺寸应尽可能接近,图3.1c中的网格较宜,图3.1d中的网格不宜。
(4)曲线边界单元可以近似用直线边代替。
(5)确定合适单元的尺寸,兼顾精度与计算成本 单元划分细小,节点数增加,计算精度越高,计算规模增大,计算时间长。一般地,在应力梯度较大的区域单元划分得细小些;应力梯度小的区域,单元可以划分得大些。可在初步分析的基础上,对于高应力区域再进一步细化网格,进行二次分析。
(6)具有不同厚度或两种材料的结构 应先按厚度或材料不同来分区,在不同区域内分别划分网格,使每个区域内的单元具有相同厚度或材料,过渡区必须遵循共边、共点的原则。
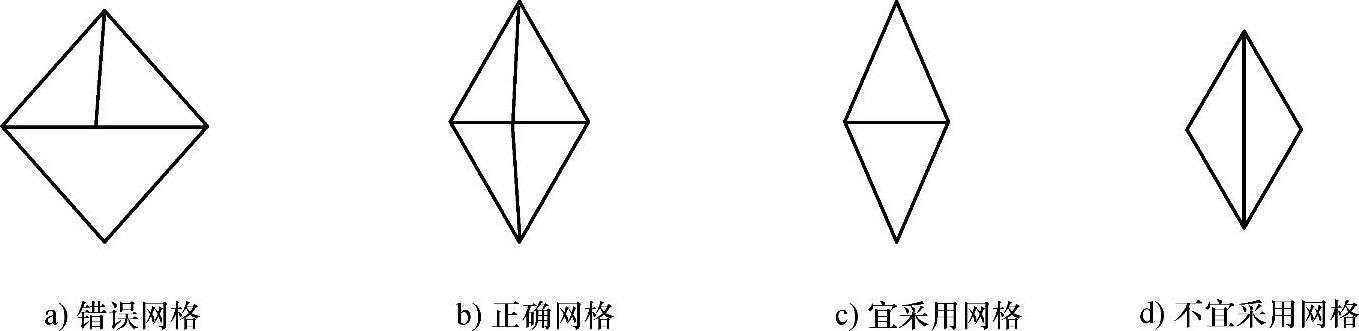
图3.1 典型网格划分
计算模型数据化,就是将离散化后的物体或结构采用数字方式表达出来,能反映出物体或结构的原始状态,即为有限元计算模型。为了完整描述原始结构的性质、形状、受力状态等,使有限元模型与原始实体模型一致,有限元模型数据应包括问题属性、节点坐标、单元构成、位移约束、外部载荷等数据。
该类数据包括问题属性、材料属性和有限元模型总体规模数据。①问题属性指的是,求解的弹性力学平面问题属于平面应力问题或是平面应变问题,可用一个符号表示问题属性,如规定pm=1表示平面应力问题,pm=2表示平面应变问题;②材料属性指的是材料的弹性模量、泊松比、重度、厚度等;③有限元模型总体规模数据,就是描述有限元网格模型中节点总数、单元总数、约束总数、集中载荷数、体力组数、分布载荷边线及节点数目等总体概况的数据。
划分单元网格之后,需要对节点进行编号。所有节点必须统一编号,从1开始按自然数顺序依次编号,序号不要间隔,更不能重复,节点不要遗漏或重编,最后的节点号同时也表示节点总数。若某节点有两个编号,则认为是两个节点,在后续主从节点分析时,采用这种编号方式。原则上节点编号顺序是任意的,以方便查找为宜。但对于大型问题,为节省存储空间,提高计算效率,应尽量使构成单元的每组节点编号差相等或相近,以单元内节点编号差最小为好,对于细长结构,宜沿着结构尺寸较短的方向进行顺序编号。
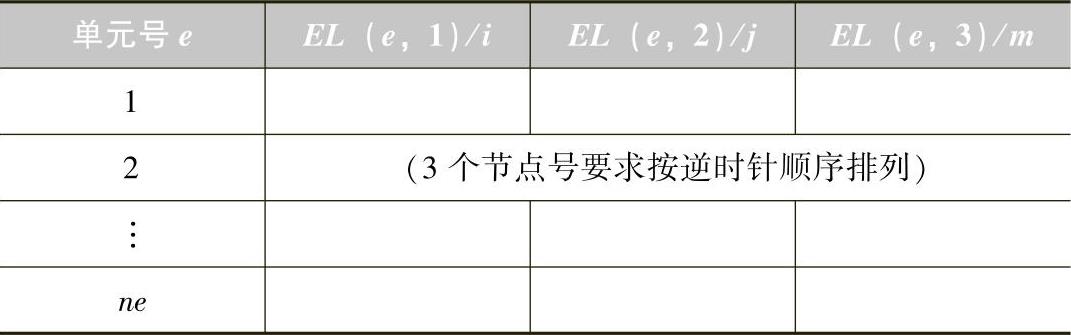
编号之后,依次将节点的坐标值有序排列成数组。二维问题,可用一个2列的二维数组或用两个一维数组,分别表示两个轴的坐标值,数组行数为节点总数,如表3.1所示(表中, node 为节点总数)。
结构离散化的作用是将原始连续的实体结构划分成形状、大小不尽相同的单元。需要对每个单元进行编号,单元编号应从1开始按自然数顺序依次进行。如果选用两种以上类型的单元时,则须按不同单元类型分别从1开始进行编号,如模型中有三角形单元和四边形单元,则三角形单元单独编序、四边形单元单独编序。
描述单元构成信息的数据就是围成单元的节点编号,按单元编号的顺序,逐一将构成单元的各个节点号 按逆时针顺序排列 起来。如三角形单元为3个节点,采用一个3列的二维数组表示,同一行上的3列元素表示一个单元的3个节点号,必须按逆时针有序填写,数组行数为单元总数,如表3.2所示(表中, ne 为单元总数)。
表3.1 节点坐标值
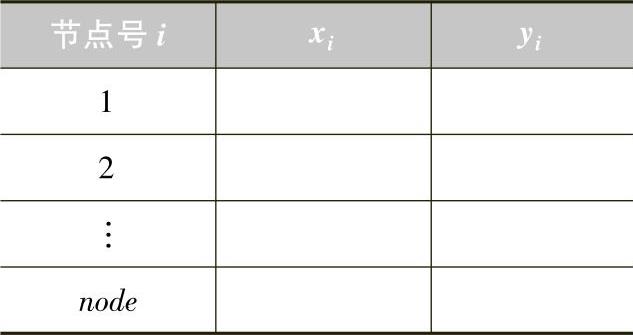
表3.2 单元信息数据
节点位移约束就是限制物体运动的边界条件,应根据结构受力特征以及支座节点对其运动的限制作用来确定,包括约束点的位置和限制位移的方向。对有限元模型中的每个位移约束进行编号,若一个节点上存在多个方向位移约束时,则必须按约束方向分别对其进行编号。如某个支座节点在 x 和 y 方向均有位移限定条件,该节点的位移约束为2,则该点有两个位移约束序号。
边界条件限定的位移值通常为“0”,则位移约束的数据只要能够表明约束位置和约束方向即可。但有时限定的节点位移不为“0”,如在平地上停放的汽车,四轮约束位移均可为“0”;若其中某个车轮在凸台或凹坑位置时,该轮位移值不应为“0”。若存在非零位移约束,则应标明约束位移的大小和符号,与坐标轴正向一致时为正。因此,描述支座的约束数据可用一个3列的二维数组表示,依次表达每个位移约束的位置、约束方向、给定的位移值。如表3.3所示,数组 BC ( nG ,3),其中 nG 为约束总的数目,第1列为约束的位置,由节点号表示;第2列为限定位移的方向代码,方向代码应统一规定,不妨规定约束 x 方向为“1”,约束 y 方向为“2”;第3列为给定位移的大小。考虑到非零位移较少,为减少数据量,只需要列出非零位移值,零位移可不填写在表3.3的第3列中,程序会自动处理。
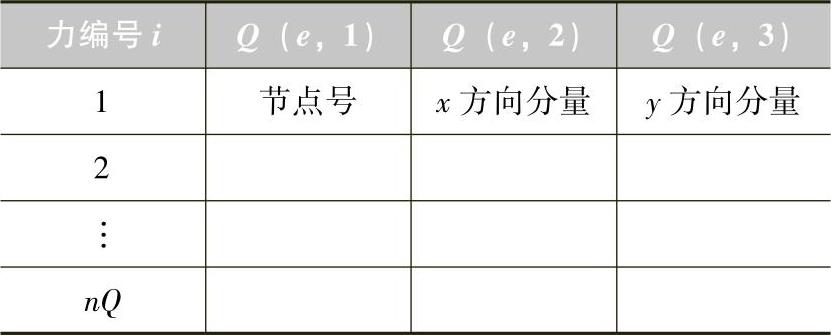
力有三要素,即作用点、作用方向和大小,力作用方向由在坐标轴上的分量确定。对集中力按作用点位置不同进行逐一编号。描述集中力的数据可用一个3列的二维数组表示,如表3.4所示,数组 Q ( nQ ,3),其中 nQ 为集中力的个数,第1列为集中力作用的位置,由节点号表示;第2与第3列为集中力在 x 与 y 方向上的分量大小,规定与坐标轴正向一致时为正值,与坐标轴正向相反时为负值。若某个节点只在一个方向上有集中力作用,则在另一方向对应的位置处填写“0”。
表3.3 节点位移约束数据
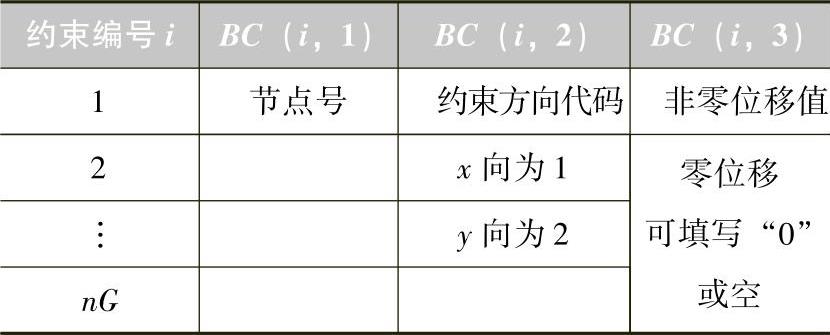
表3.4 集中力数据
弹性体所受的表面力通常只在部分边界上存在且不均匀分布,描述表面力时,需要指明有表面力的单元边界及其面力的大小。平面单元的边界由两端的节点号表示;若面载荷为线性分布时,需要指明边界两端节点处的面力大小。因此,描述线性分布面载荷的数据需要有4个,即单元边界两端的节点编号以及相应节点处面力的大小。有两种表达方案:
第一方案,用一个4列的矩阵表示,其中两列表示单元边界两端的节点编号,另两列表示对应节点处的面力大小,矩阵行数与存在表面力单元边的个数相同,每一行表示一段边界载荷数据。这种逐段描述的方法,对编程而言直观方便,但因节点连接两个单元,因此每个节点数据需要输入两次。
第二方案,为解决第一方案重复输入问题,采用两个矩阵组合表示,具体方法参见表3.7和表3.8。
有限元模型数据填写格式与程序的数据输入格式要求必须对应。需要指出,在编写有限元模型数据之前,应先明确采用的单位制,确定各个物理量的基本单位,将各种量的数据转换为基本单位。如常采用mm-N单位制,即长度单位为mm、力的单位为N,计算结果的应力单位为MPa(N/mm 2 );若采用m-N单位制,即长度单位为m、力的单位为N,则应力单位为Pa(N/m 2 )。