





Abstract: A three-dimensional (3-D) modified cellular automaton (MCA) method was developed for simulating the dendrite morphology of cubic system alloys. Two-dimensional (2-D) equations of growth velocities of the dendrite tip, interface curvature and anisotropy of the surface energy were extended to 3-D system in the model. Therefore, the model was able to describe the morphology evolution of 3-D dendrites. Then, the model was applied to simulate the mechanism of spacing adjustment for 3-D columnar dendrite growth, and the competitive growth of columnar dendrites with different preferred growth orientations under constant temperature gradient and pulling velocity. Directional solidification experiments of NH 4 Cl-H 2 O transparent alloy were performed. It was found that the simulated results compared well with the experimental results. Therefore, the model was reliable for simulating the 3-D dendrite growth of cubic system alloys.
Key words : modified cellular automation; 3-D dendrite morphology; dendrite growth; directional solidification; NH 4 Cl-H 2 O transparent alloy
The initial dendrite microstructure during solidification has significant influence on the properties of the castings. There are several approaches to investigate the mechanism of the dendrite evolution, such as experimental studies, theoretical approaches and numerical technique. The adjustment of primary dendrite arm spacing ( λ 1 ) was observed by experimental research on transparent alloys [1-3] .Meanwhile, several theoretical models [4-6] were developed to describe the relationship between λ 1 and the solidification parameters (temperature gradient, G ,and solidification rate, v ). However, it is well known that the classical experimental and theoretical approaches are unable to describe the detailed microstructure phenomena including the branching and coarsening of secondary dendrite arms.
Recently, the phase field (PF) model and the cel lular automaton (CA) approach have presented their considerable potential for quantitatively describing realistic phenomena associated with dendrite growth, including side arm branching and coarsening. KARMA and RAPPEL [7] studied the effect of surface anisotropy on the 3-D dendrite morphologies by a phase field model. NESTLER et al [8] developed a phase field model to simulate the crystal growth in a pure substance for different initial undercoolings. However, the algorithm of phase field model is complicated and the computational efficiency is lower. The CA model is more computationally efficient than the phase field model, because the computing grid can be coarser in CA model. Therefore, CA model is rapidly emerging as a choice for simulating the dendrite formation in solidification of commercial alloys [9-13] .YUAN and LEE [14] studied the effect of fluid motion on the 3-D dendrite morphology of Ni-4.85%Nb alloy by coupling CA model with basic flow equations, but the model ignored the anisotropy of interface energy. PAN and ZHU [15] developed a 3-D CA model to simulate the effect of melt undercoolings and degrees of anisotropy of interface energy on the single dendrite morphologies of Fe-0.6%C alloy. CHEN and XIONG [16] developed a simple CA method to simulate columnar dendrite transformation to equiaxed dendrite (CET) of twin-roll continuous casting aluminum thin strip.
In the present study, a 3-D modified cellular automaton (MCA) model was developed to simulate the 3-D dendrite evolution in solidification of alloys based on the 2-D CA model. It proposed a simplified solution of the anisotropy of interface energy, which can affect the curvature undercooling and the dendrite morphology. Competitive growth of 3-D columnar dendrites in directional solidification was simulated by the model. In order to validate the model, the simulated results were compared with those derived by experiments.
In the 3-D MCA model, the domain is meshed by a set of uniform cubic cells, and the cell is characterized by the solid fraction ( f S ):liquid ( f S =0), solid ( f S =1) or interface (0< f S <1).
During the solidification process, for an alloy the solute diffusion is solved in the liquid and solid region, respectively, which is governed by
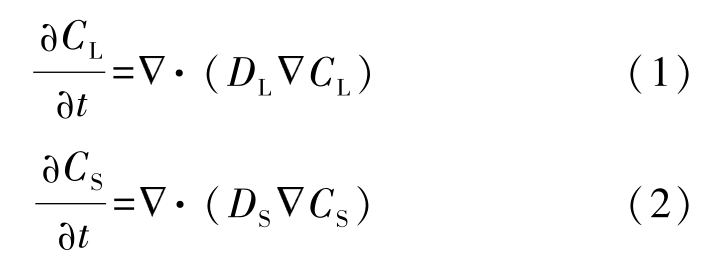
where C and D are the composition and solute diffusion coefficient, and the subscripts "L" and "S" means the liquid and solid, respectively, t is time, and k 0 is the solute partition coefficient.
At the micro-scale level, the relationship between the equilibrium composition and the interface temperature is given by [17,18]
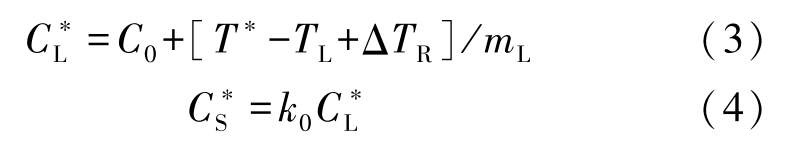
where
T
*
is the interface temperature,
T
L
is the liqui dus temperature,
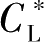 and
and
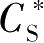 are the equilibrium liquid and solid composition, respectively,
C
0
is the initial composition, Δ
T
R
is the curvature undercooling, and
m
L
is the slope of the liquidus line.
are the equilibrium liquid and solid composition, respectively,
C
0
is the initial composition, Δ
T
R
is the curvature undercooling, and
m
L
is the slope of the liquidus line.
The anisotropy of interfacial energy and the orientation dependence of the interfacial stiffness are incorporated into the equation of curvature undercooling, which can be expressed as follows [19,20] :
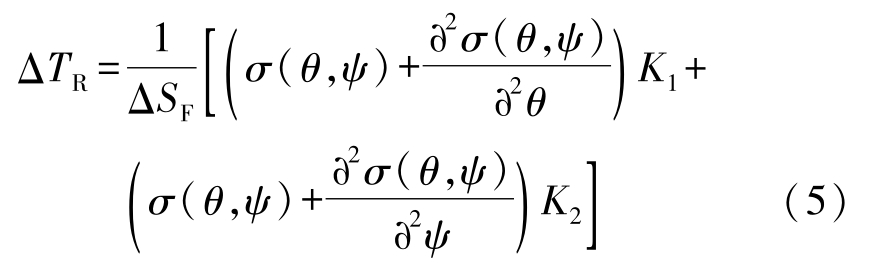
where σ ( θ , ψ ) is the anisotropic interfacial free energy, θ and ψ are the two standard spherical angles of the normal to the solid-liquid interface. In a rectangular Cartesian coordinate system, θ is the angle between normal to the solid-liquid interface and z axis, and ψ is the normal projection in the x—y plane with respect to the x axis. K 1 and K 2 are the two principal interfacial curvatures.Δ S F is the melting entropy of the alloys.
To simulate the growth of the typical cubic dendrites, a general form of the anisotropy function of interfacial energy with equal strength of anisotropy in the basal and in normal direction is given by [21,22]
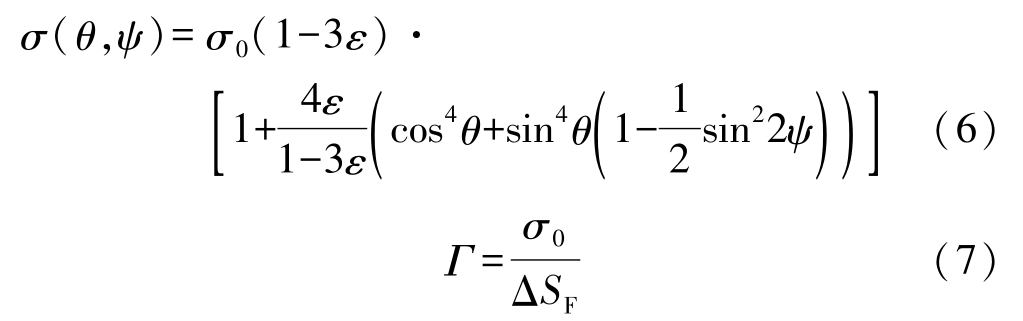
where σ 0 is the isotropic interfacial energy, Г is the Gibbs-Thomson coefficient, and ε is the anisotropic coefficient.
In order to calculate θ and ψ , the unit vector normal to the interface η is simplified as follows:
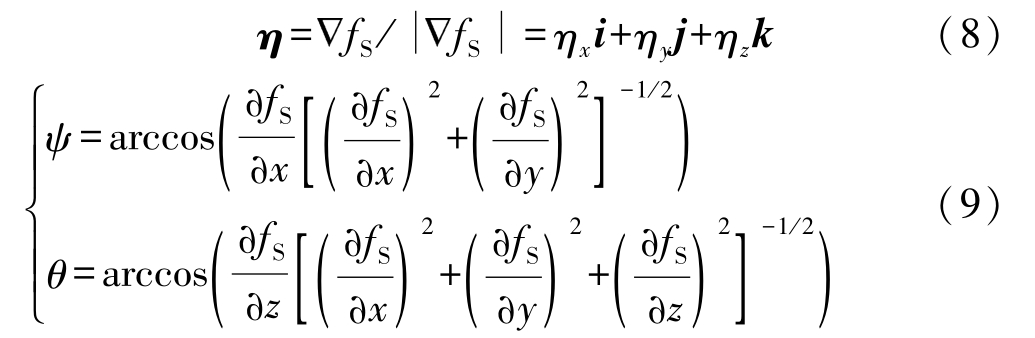
where η x , η y and η z are the rectangular components of the vector η .
The interface root mean square curvature of CA interface cell is calculated by a simplified computational method.
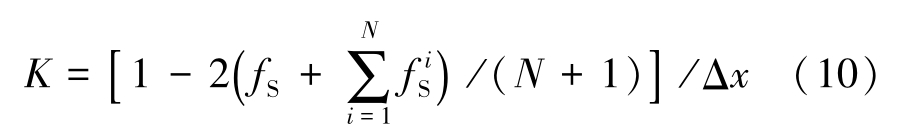
where Δ
x
is the cell size,
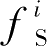 is the solid fraction of the neighboring cells, and
N
is the total number of CA cells counted around the interface cell. In a 3-D system,
N
equals 26.
is the solid fraction of the neighboring cells, and
N
is the total number of CA cells counted around the interface cell. In a 3-D system,
N
equals 26.
Solute conservation at the S/L interface is given by
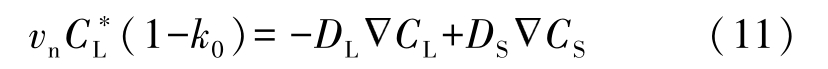
where v n is the normal velocity of the interface. In three dimensional condition, v n =( v x , v y , v z ), which can be expressed as
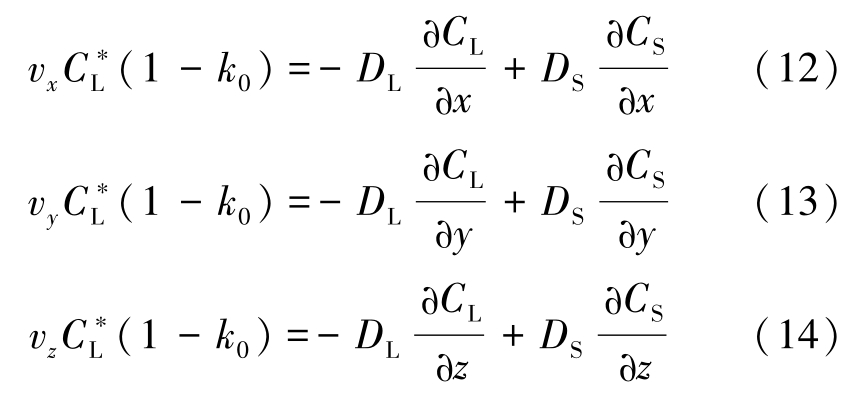
After calculating the velocity components in x -, y -and z -directions, the increment of solid fraction at the interface is obtained by
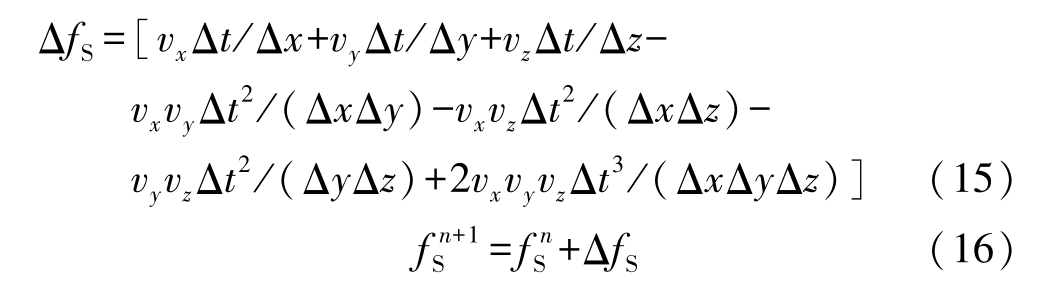
where
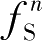 and
and
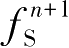 are the solid fraction at the current time step and the next time step, respectively. When
f
S
equals 1, the interface cell becomes solid and captures the neighboring liquid cells, and the captured cells change its state to interface. Therefore, the dendrite can grow.
are the solid fraction at the current time step and the next time step, respectively. When
f
S
equals 1, the interface cell becomes solid and captures the neighboring liquid cells, and the captured cells change its state to interface. Therefore, the dendrite can grow.
As shown in Fig. 1, NH 4 Cl-H 2 O transparent alloy was poured into a sample cell, and then subjected to directional solidification under constant pulling velocity ( v p ) in a horizontal heating and cooling system, which can supply a constant temperature gradient ( G ). During the directional solidification process, the dendrite growth was observed by a microscope in real time.
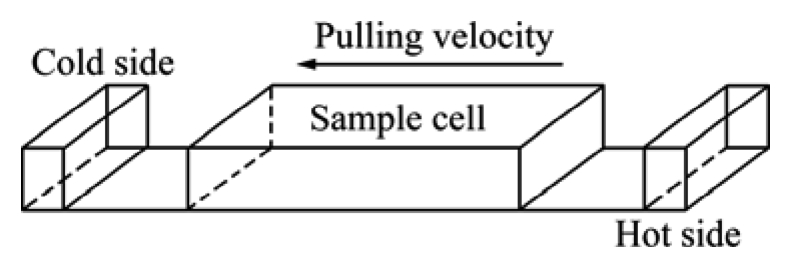
Fig. 1 Schematic illustration of experimental setup for directional solidification of NH 4 Cl-H 2 O transparent alloy
The thermal diffusion is several orders higher than the solute diffusion. Therefore, in the calculation domain, the temperature is controlled by G and v p .
In order to validate the MCA model, the directional solidification of an NH 4 Cl-74%H 2 O (mass fraction) transparent alloy was simulated. The material properties were derived from Ref.[17].
At first, several seeds were set at the base x—y plane and the preferred growth direction of all the seeds aligned well with z -axis. The solidification parameters were used as follows: G =1K/mm, v p =3μm/s, which were the same as experiments. The calculation domain was 1.8mm×0.12mm×2.4mm with cell size of 6μm.
From Fig. 2, it can be seen that two primary dendrite arms developed well. Some tertiary dendrites emanated from the secondary dendrite arms. However, they were blocked by the other secondary dendrites both from simulation (see Fig. 2(a)-(c)) and experimental result (see Fig. 2(d)). The two primary dendrites kept growing, the secondary arms began to coarsen, and the spacing remained constant (see Fig. 2(e)-(h)). Above all, the simulated results agreed well with the experimental results.
Similar to the preliminary 3-D simulation of 2 seeds, the growth of 3 seeds at different time steps was simulated (see Figs.3(a) and (e)) and observed by experiments (see Figs.3(d) and (h)). At the beginning of simulation,3 seeds were nucleated at the bottom with the <100> directions aligned well with z -axis, and the distance of the 2 seeds at the left side (see Figs.3(c) and (d)) was closer than the right 2 seeds. Because of the dense packing of the left 2 seeds, the growth of one seed was suppressed after initial competition. It can be seen that, two dendrites with the same preferred growthdirection overgrew the left one and kept growing steadily (see Figs.3(a) and (e)). It was found that the experimental dendrites (see Figs.3(d) and (h)) agreed well with that simulation (see Figs.3(c) and (g)). Therefore, the MCA model can simulate the competitive growth of dendrites.
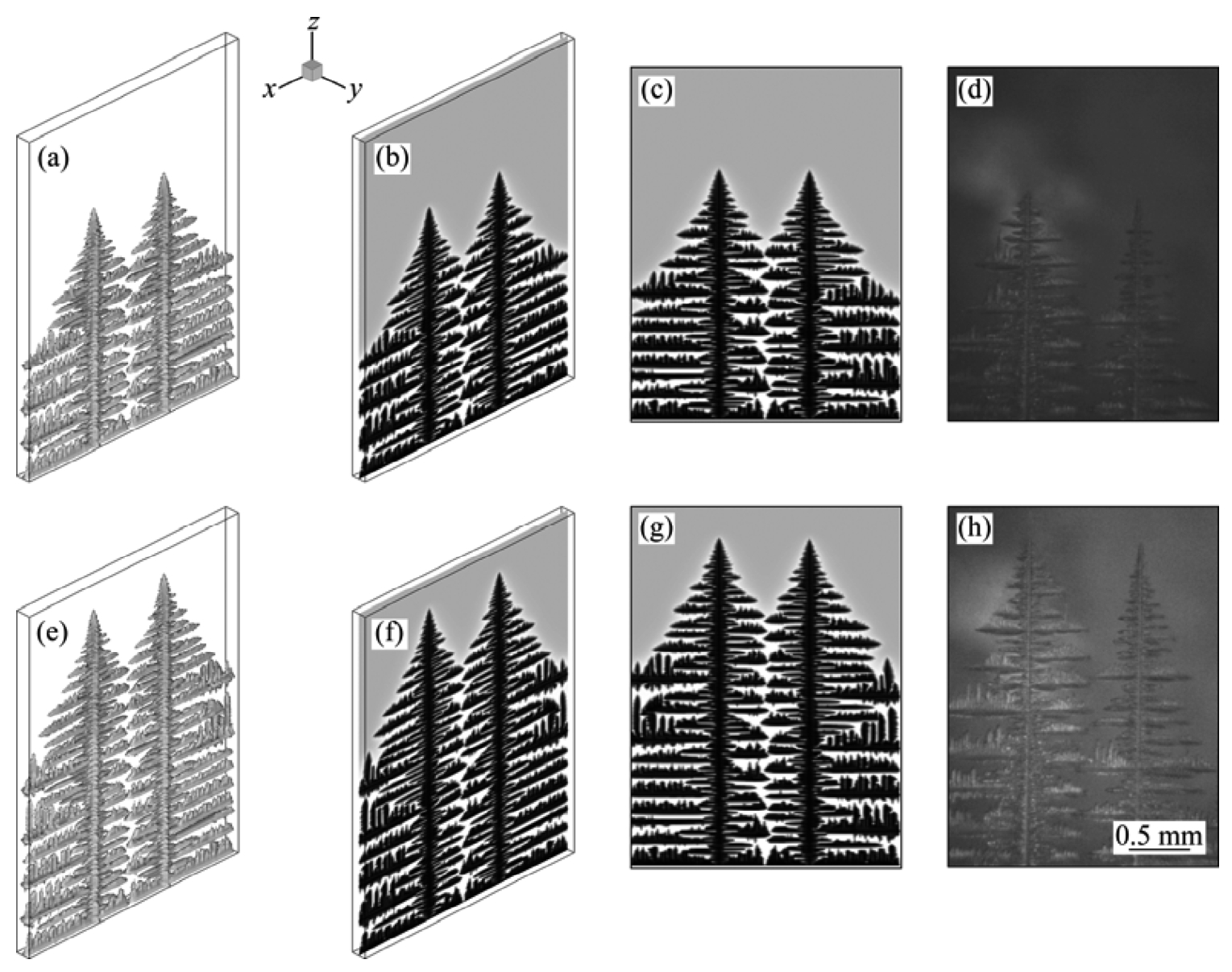
Fig. 2 Simulated and experimental results of 3-D columnar dendrite growth of NH 4 Cl-74%H 2 O transparent alloy with 2 seeds in directional solidification:(a) t =430s, 3-D morphology; (b,c) t =430s, x—z central slice of the solute field; (d) Experimental photograph; (e) t =740s, 3-D morphology; (f,g) t =740s, x—z central slice of the solute field; (h) Experimental photograph
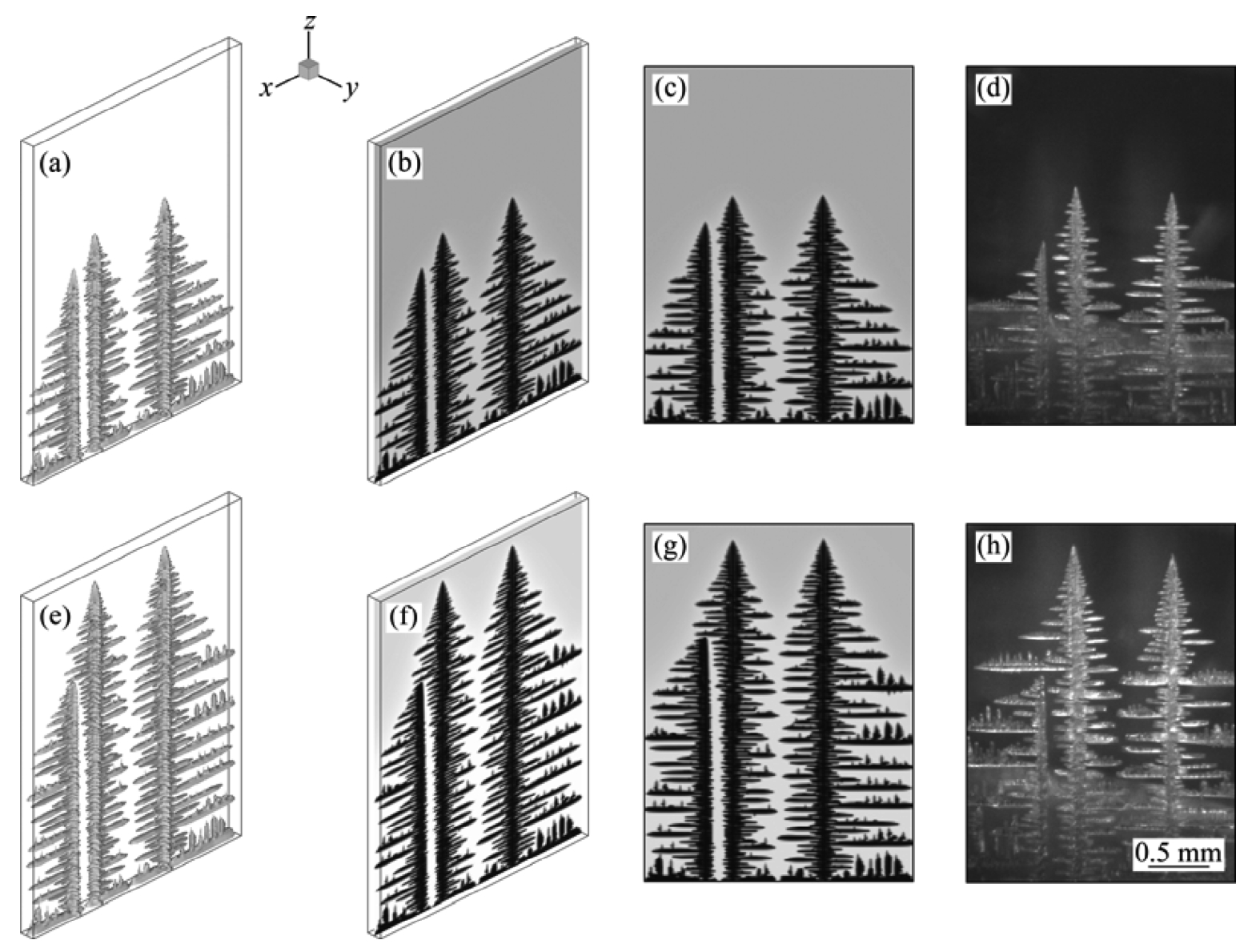
Fig. 3 Simulated and experimental results of 3-D columnar dendrite growth of NH 4 Cl-74%H 2 O transparent alloy with 3 seeds: (a) t =420s, 3-D morphology; (b,c) t =420s, x—z central slice; (d) Experimental photograph; (e) t =750s, 3-D morphology; (f,g) t =750s, x—z central slice; (h) Experimental photograph
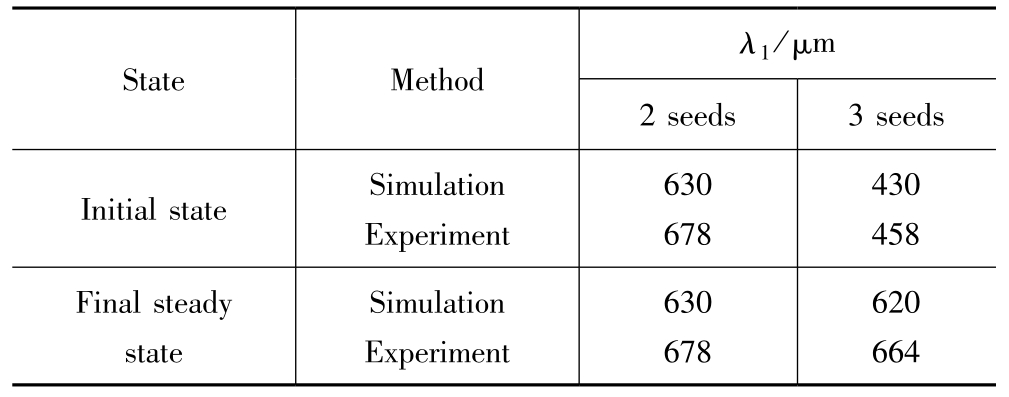
In classical models [4-6] , the growth of dendrites with different numbers of seeds could result in the same final primary dendrite arm spacing ( λ 1 ) when the solidification parameters were constant. λ 1 was determined as function of G and solidification rate v ( v ≈ v p ), λ 1 ∝ G -0.5 v -0.25 .From Table 1, it can be seen that a smaller dendrite was overgrown by its neighbors when the initial spacing was too narrow, and the final primary dendrite arm spacing in the simulation compared well with the experimental results.
Table 1 Comparison of final primary dendrite arm spacing ( λ 1 ) between initial and final state under constant G and v p
The simulation and experiment of competitive growth of columnar dendrites in a 3D block were performed with G =1K/mm, and v p =10μm/s. In this 3-D simulation, temperature gradient stood perpendicularly to the x—y plane. The calculation domain consisted of 300×20×400 CA cells and the cell size was 6μm. At the beginning,4 seeds were set at the bottom plane with different preferred growth directions, and 2 seeds at the left wall were favorably oriented.
It can be seen that two dendrites aligned well with z -axis had the maximum growth rate (see Figs.4(a) and 4(d)), and they were the leading dendrites, which grew faster than the dendrites with misaligned orientations (Figs.4(e) and (h)). Finally, the development of secondary dendrite arms on the leading dendrites exceeded the tip of the lagging dendrite, and suppressed the growth of the lagging dendrites, which had the misaligned orientations. It was obvious that the predicted dendrite pattern was in good agreement with that obtained by experiments (see Fig. 4).
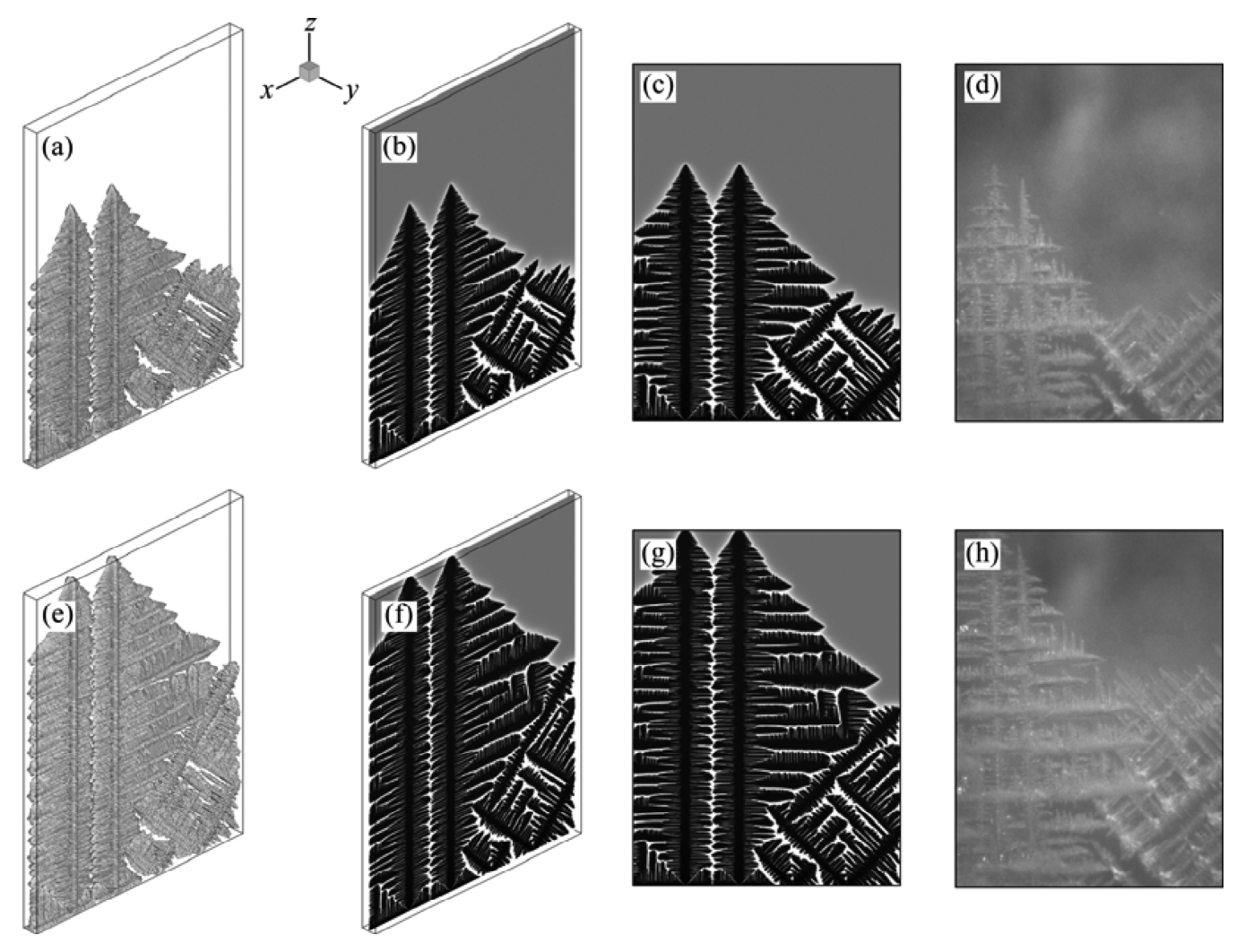
Fig. 4 Competitive growth of columnar dendrite of NH 4 Cl-74%H 2 O transparent alloy with different preferred growth orientations: (a) t =160s; (b,c) t =160s, x—z central slice; (d)Experimental result; (e) t =220s; (f,g) t =220s, x—z central slice; (h)Experimental result
A 3-D MCA model for the simulation of columnar dendrite growth in directional solidification process was developed. A simplified computational method of anisotropic interfacial energy was imported into the present model. The normal velocity of the interface was derived by solving the 3-D solute conservation equation subjected to the boundary conditions at the S/L interface. The MCA model was applied to simulate the selection and competition of columnar dendrites in directional solidification of NH 4 Cl-H 2 O transparent alloy. It was found that initial seed numbers had little effect on the primary dendrite arm spacing when the dendrite growth reached a stable state. It was also found that the crystal orientation parallel to heat flow direction can overgrow the misaligned one, which yield a relatively good quantitative agreement with experimental results. Above all, the present 3-D MCA model is possible to be a powerful tool to predict a number of interesting microstructure pattern formation issues of commercial alloys.
[1]SOMBOONSUK K, TRIVEDI R. Dynamical studies of dendritic growth [J].Acta Metall,1985, 33(6):1051-1060.
[2]SUKY M J, PARK Y M, KIM Y C. Dendrite spacing selection during directional solidification of pivalic acid-ethanol system [J].J Mater Sci Technol,2008, 24(3):340-342.
[3]WAN X, HAN Q, HUNT J D. Different growth regimes during directional dendritic growth [J].Acta Mater,1997, 45(10):3975-3979.
[4]LU S Z, HUNT J D. Numerical modeling of cellular/dendritic array growth: Spacing and structure predictions [J].Metall Mater Trans A,1996, 27:611-623.
[5]KURZ W, FISHER D J. Dendritic growth and limit of stability tip radius and spacing [J].Acta Metall,1981, 29:11-20.
[6]TRIVEDI R. Interdendritic spacing:part II. A comparison of theory and experiment [J].Metall Mater Trans A,1984, 15(6):977-982.
[7]KARMA A, RAPPEL W J. Quantitative phase-field modeling of dendritic growth in two and three dimensions [J].Phys Rev E,1998, 57(4):4324-4349.
[8]NESTLER B, DANILOV D, GALENKO P. Crystal growth of pure substances: Phase-field simulations in comparison with analytical and experimental results [J].Journal of Computational Physics,2005, 207:221-239.
[9]NASTAC L. Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys [J].Acta Mater,1999, 47:4253-4262.
[10]BELTRAN-SANCHEZ L, STEFANESCU D M. Growth of solutal dendrites: A cellular automaton model and its quantitative capabilities [J].Metall Mater Trans A,2003, 34(2):367-382.
[11]WANG W, LEE P D, MCLEAN M. A model of solidification microstructures in nickel-based superalloys: Predicting primary dendrite spacing selection [J].Acta Mater,2003, 51:2971-2987.
[12]LIU B C, XIONG S M, XU Q Y. Study on macro-and micromodeling of the solidification process of aluminum shape casting [J].Metall Mater Trans B,2007, 38:525-532.
[13]LI B, XU Q Y, PAN D, LIU B C, XIONG Y C, ZHOU Y J, HONG R Z. Microstructure simulation of ZL114A alloy during low pressure die casting process [J].Acta Metall Sin,2008, 44(2):243-248. (in Chinese)
[14]YUAN L, LEE P D. Dendritic solidification under natural and forced convection in binary alloys: 2D versus 3D simulation [J].Modelling Simul Mater Sci Eng,2010, 18:055008.
[15]PAN S Y, ZHU M F. A three-dimensional sharp interface model for the quantitative simulation of solutal dendritic growth [J].Acta Mater,2010, 58:340-352.
[16]CHEN S D, XIONG S M. Simulation of microstructures in solidification of aluminum twin-roll casting [J].Transactions of Nonferrous Metals Society of China,2012, 22(6):1452-1456.
[17]SHI Y F, XU Q Y, GONG M, LIU B C. Simulation of NH 4 Cl-H 2 O dendritic growth in directional solidification [J].Acta Metall Sin,2011, 47(5):620-627. (in Chinese)
[18]WU M W, XIONG S M. Modeling of equiaxed and columnar dendritic growth of magnesium alloy [J].Transactions of Nonferrous Metals Society of China,2012, 22(9):2212-2219.
[19]NAPOLITANO R E, LIU S, TRIVEDI R. Experimental measurement of anisotropy in crystal-melt interfacial energy [J].Interface Science,2002, 10:217-232.
[20]NAPOLITANO R E, LIU S. Three-dimensional crystal-melt Wulff-shape and interfacial stiffness in the Al-Sn binary system [J].Phys Rev B,2004, 70:214103-1-11.
[21]JEONG J H, DANTZIG J A, GOLDENFELD N. Dendritic growth with fluid flow in pure materials [J].Metall Mater Trans A,2003, 34(3):459-466.
[22]ZHAO D P, JING T, LIU B C. Simulating the three-dimensional dendritic growth of Al alloy using the phase-field method [J].Acta Phys Sin,2003, 52:1737-1742. (in Chinese)