由磁刚度非线性隔振器的原理图可以看出,多个环形永磁体之间通过非线性磁力传递力,为了定性且定量地描述其隔振性能,有必要得到非线性磁力的计算表达式。图3-8为非线性隔振器的环形永磁体之间的相对位置关系及磁场分布。环形永磁体间的非线性磁力计算极为复杂,本节将基于第2.4节给出的非线性磁力模型进行计算。
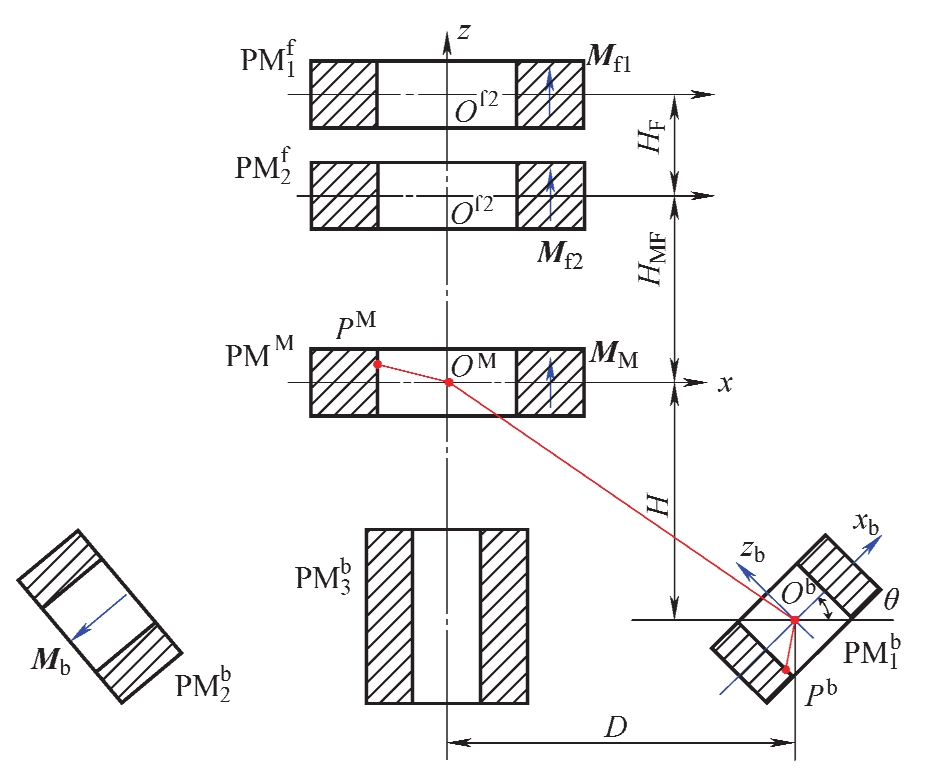
图3-8 环形永磁体之间的相对位置关系及磁场分布
假设所有的环形永磁体均沿各自轴向均匀磁化,则永磁体
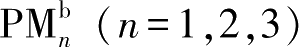 、PM
M
、
、PM
M
、
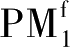 和
和
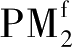 的磁化矢量分别为
M
b
n
,
M
M
,
M
f1
和
M
f2
。根据动磁体和不动磁体间的吸力和斥力特性,可知,三个环形永磁体PM
b
与
的磁化矢量分别为
M
b
n
,
M
M
,
M
f1
和
M
f2
。根据动磁体和不动磁体间的吸力和斥力特性,可知,三个环形永磁体PM
b
与
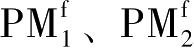 和PM
M
之间的总非线性磁力为
和PM
M
之间的总非线性磁力为
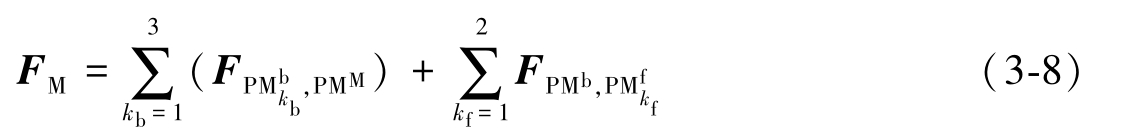
其中,
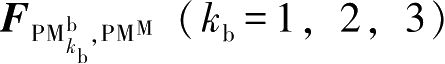 为第
k
b
个永磁体PM
b
与永磁体PM
M
产生的总非线性磁力;
为第
k
b
个永磁体PM
b
与永磁体PM
M
产生的总非线性磁力;
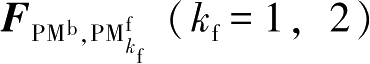 为第
k
f
个环形永磁体PM
f
与三个环形永磁体PM
b
间的总非线性磁力;
为第
k
f
个环形永磁体PM
f
与三个环形永磁体PM
b
间的总非线性磁力;
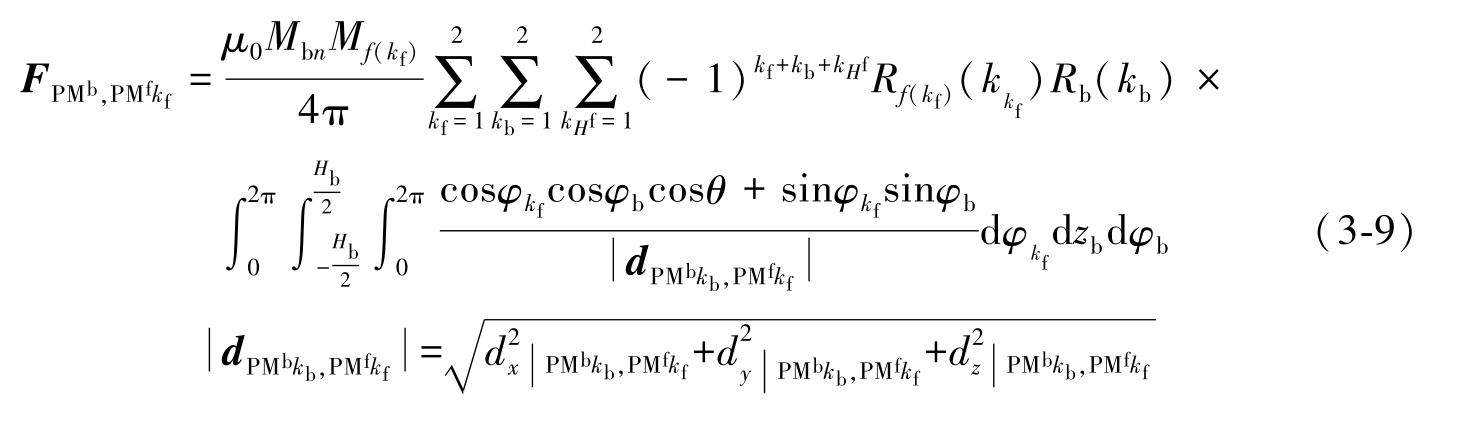
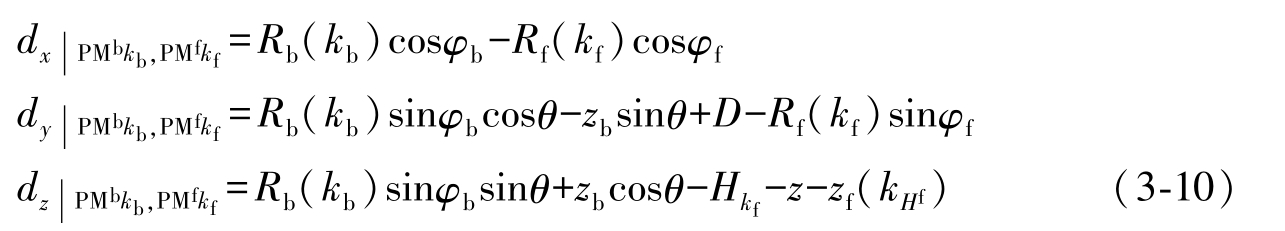
其中, H 1 = H + H MF , H 2 = H + H MF + H F 。
根据式(2-24),磁刚度非线性隔振器的等效磁刚度为
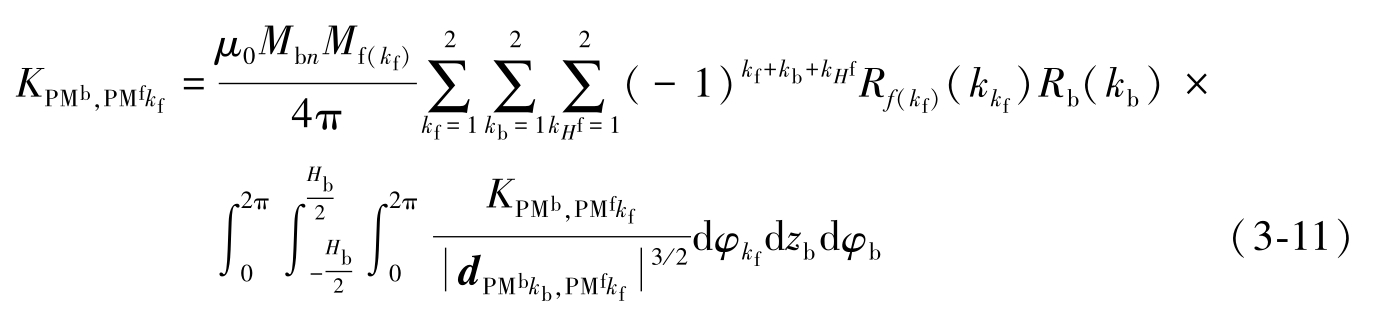
因此,非线性磁力所产生的磁刚度为

借助第2章得到的非线性磁力近似解析表达式,本小节着重分析磁刚度非线性隔振器的非线性磁恢复力及磁刚度特征。隔振器可以通过调节图3-8中的 D 、 H 和 θ 来调节非线性磁力,因此,有必要分析不同结构参数对非线性磁力和磁刚度的影响规律,以实现隔振性能的优化。本章将采用表3-1给出的环形永磁体参数进行数值仿真和试验研究。
表3-1 环形永磁体几何参数及剩磁强度
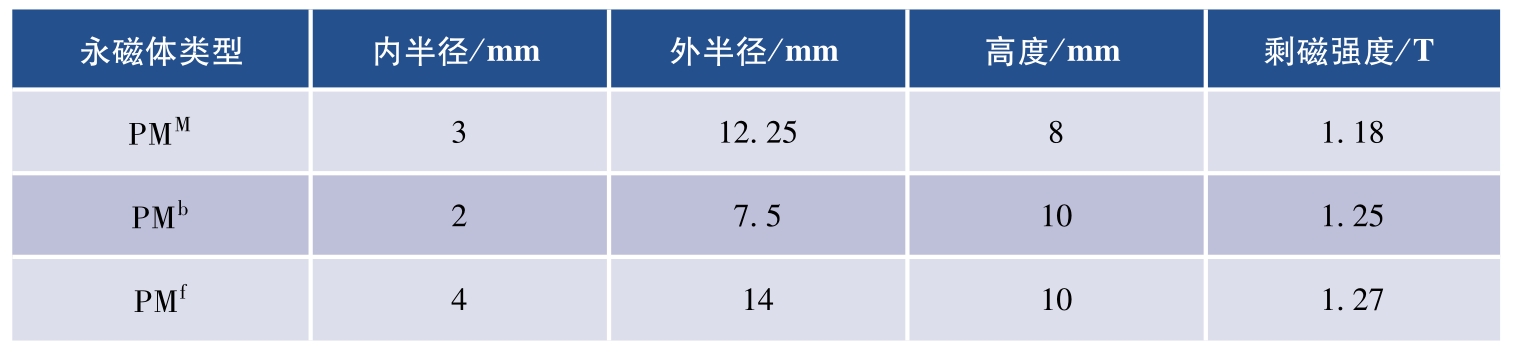
图3-9和图3-10为当PM
b
与PM
M
之间分别为斥力和吸力时,非线性磁力
F
M
随参数
D
、
H
和
θ
变化的曲线。可以看出,随参数
D
、
H
和
θ
的变化永磁力呈现强非线性特征。由于图3-7所示的三个环形永磁体
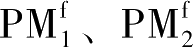 和PM
M
在
z
轴方向与永磁体PM
b
是不对称的。因此,当相对位移为负时,非线性磁力变化剧烈,当相对位移为正时,非线性磁力变化较为缓慢。此外,当参数
H
增加使得PM
M
和PM
b
的间距增大时,非线性磁力减小;反之,则非线性磁力增大。
和PM
M
在
z
轴方向与永磁体PM
b
是不对称的。因此,当相对位移为负时,非线性磁力变化剧烈,当相对位移为正时,非线性磁力变化较为缓慢。此外,当参数
H
增加使得PM
M
和PM
b
的间距增大时,非线性磁力减小;反之,则非线性磁力增大。
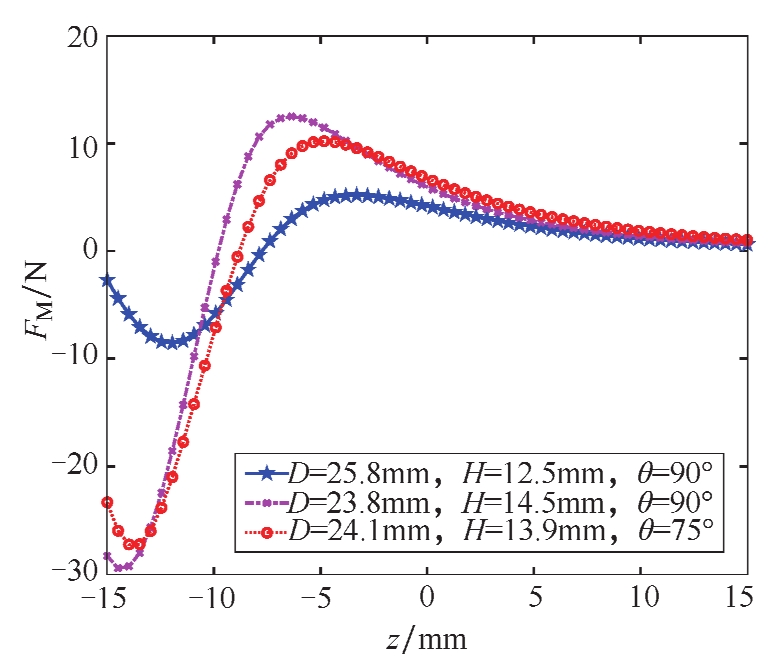
图3-9 PM b 与PM M 之间磁力为斥力时 F M 随参数 D 、 H 和 θ 的变化规律
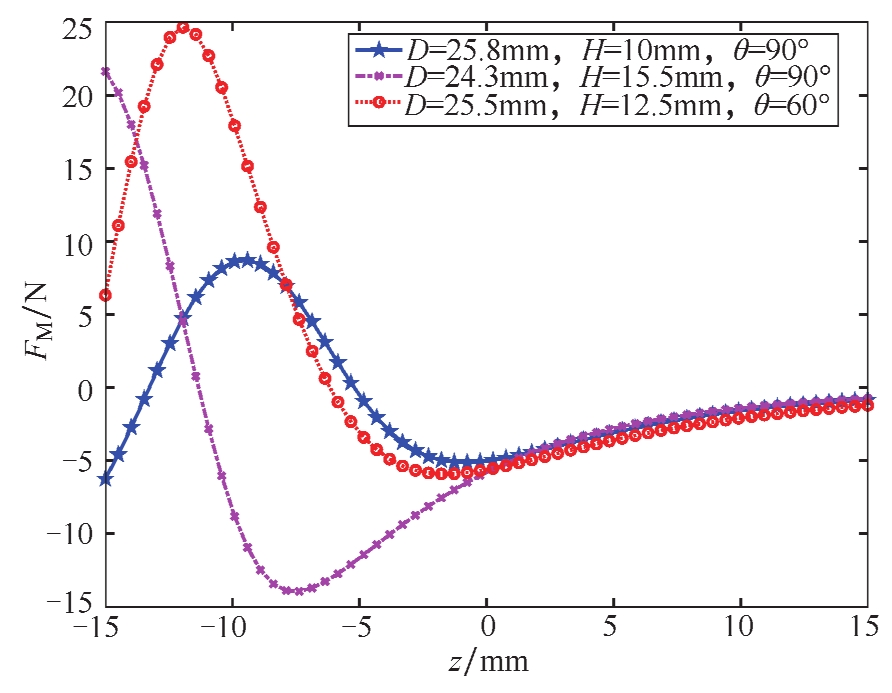
图3-10 PM b 与PM M 之间磁力为吸力时 F M 随参数 D 、 H 和 θ 的变化规律
磁刚度为非线性磁力 F M 的斜率,由图3-9和图3-10可知,隔振器在平衡位置附近的局部区域,磁刚度为负,且随 D 的减小而增大。在小扰动或者小激励作用下,非线性磁力可用多项式近似拟合为

其中, μ 和 ν 分别为磁力的等效线性和非线性刚度系数; f c 为常力,在静平衡位置处与弹簧弹性恢复力和重力相互抵消。
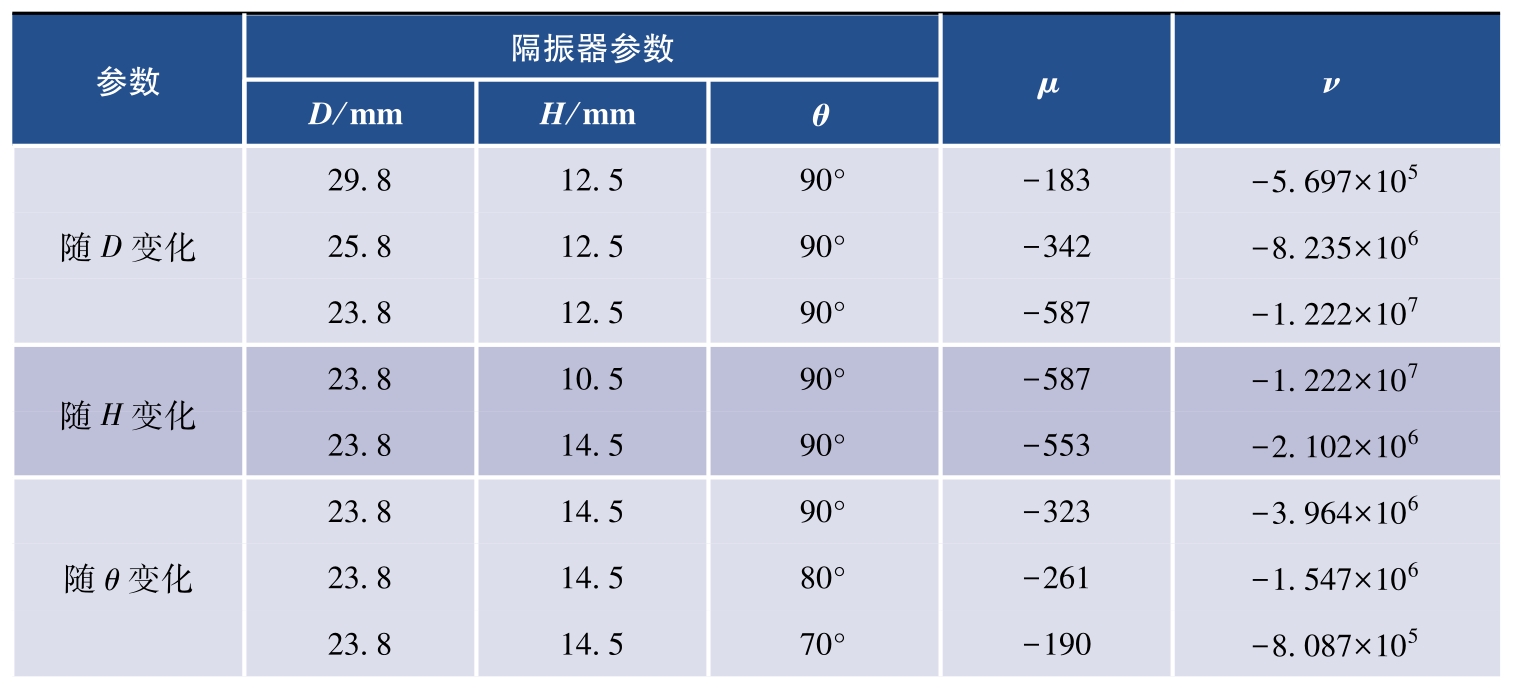
图3-11为非线性磁力的解析解和拟合曲线对比图,可知,当隔振系统的相对位移较小时,三阶多项式拟合精度满足要求。表3-2为刚度系数 μ 和 ν 随参数 D 、 H 和 θ 的变化规律,可以看出,其线性刚度系数 μ 为负,通过磁结构可以获得等效负刚度,以降低隔振系统的总刚度。此外,本设计中的非线性刚度 μ 也为负,这体现了软弹簧特性。
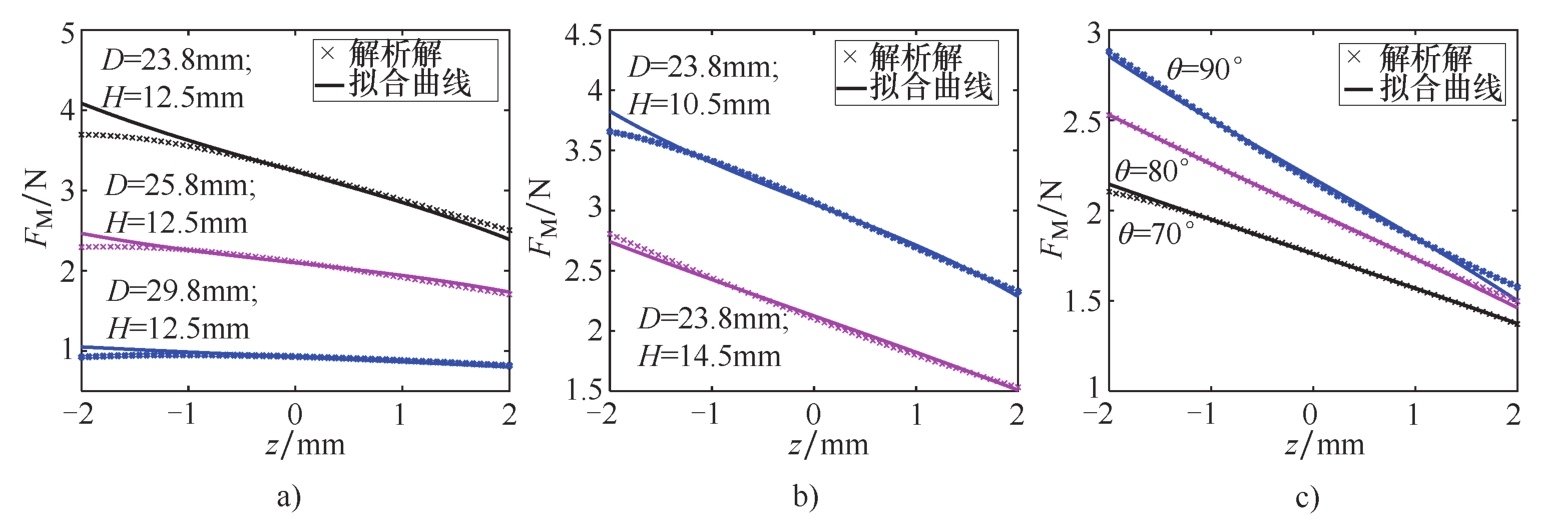
图3-11 非线性磁力的近似解析解和拟合结果对比,磁力随不同参数变化的曲线
a)参数为 D b)参数为 H c)参数为 θ
表3-2 刚度系数 μ 和 ν 随参数 D 、 H 和 θ 的变化规律