下载掌阅APP，畅读海量书库
立即打开
在空间中建立一个固定的坐标系后，该空间中的任意一个位置都可以用3×1的位置矢量表示。图3-1所示为空间位置表示。
其中， x 0 、 y 0 、 z 0 是位置矢量 p 在空间坐标系中的三个坐标分量。
对于机器人的运动控制，除了正确表示空间中某个点的位置，还需要表示物体的方位。物体的方位可以由设置在此物体上的某个坐标系描述。为了表示空间中刚体B的方位，在此刚体上设置笛卡儿坐标系{B}。坐标系{B}相对于参考坐标系{A}的方向余弦组成的3×3矩阵表示刚体B相对于坐标系{A}的方位。
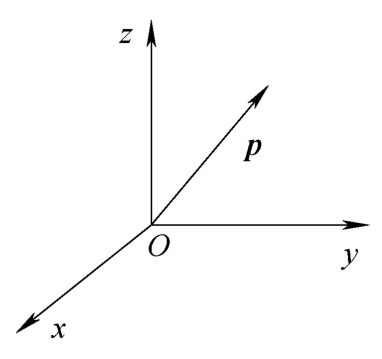
图3-1 空间位置表示
坐标系{B}相对于参考坐标系{A}的空间姿态表示如图3-2所示。
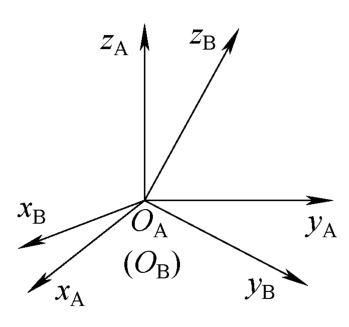
图3-2 空间姿态表示
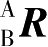称为旋转矩阵。式（3-2）中的上标A表示参考坐标系{A}，下标B表示被描述的坐标系{B}。
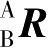共有9个元素，但只有3个是相互独立的。
对应于绕 x 、 y 或 z 轴旋转 θ 角度的位姿变化，对应的旋转矩阵分别为
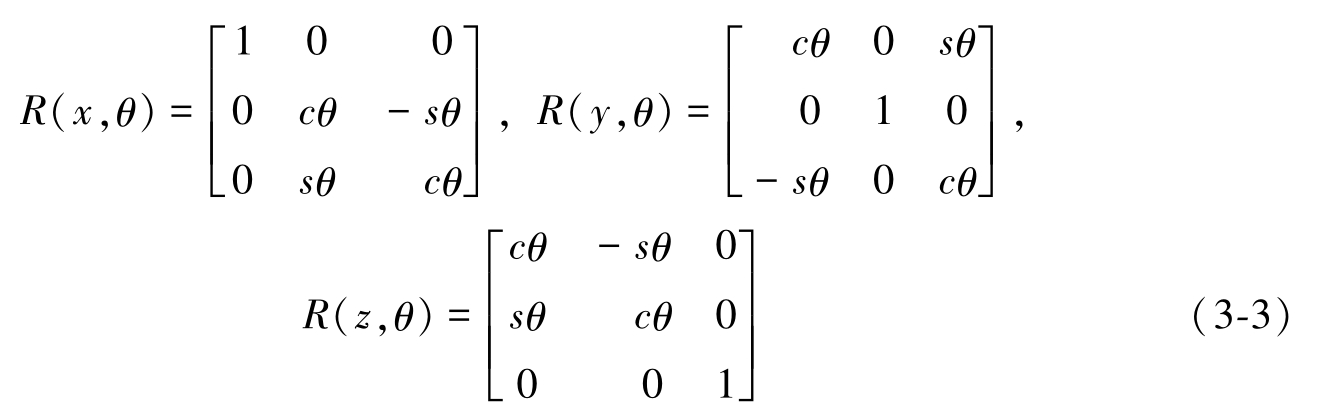
其中， s 表示sin， c 表示cos，以后章节均按照此约定。
齐次坐标是用 n+ 1维来表示 n 维坐标，则该 n+ 1维坐标即为 n 维坐标的齐次坐标。令 w 为该齐次坐标中的比例因子，当 w= 1时，其表示方法称为齐次坐标的规范化形式。
如式（3-1）对应的齐次坐标的规范化形式为
当 w ≠1时，则相当于该矩阵中各元素同时乘以一个非零比例因子 w ，但仍表示原来的点。
其中， a=wp x ， b=wp y ， c=wp z 。
1.平移齐次坐标变换
空间中某点由矢量 a i +b j +c k 描述。 i 、 j 、 k 分别为 x 、 y 和 z 轴上的单位矢量。那么，此点可用平移齐次变换表示为
例：矢量2 i + 2 j + 7 k 被矢量 i -2 j + 6 k 平移后得到的新矢量 v 1 为
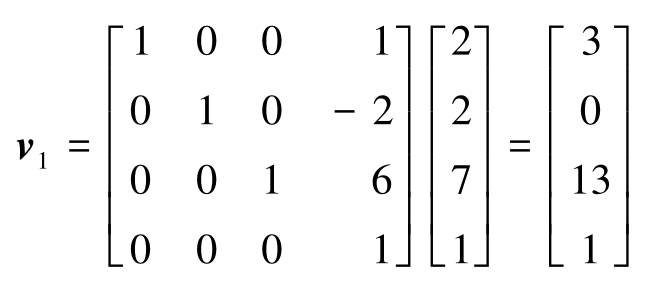
2.旋转齐次坐标变换
绕 x 、 y 或 z 轴旋转 θ 角度的位姿变化，对应的齐次旋转矩阵分别为
例：将矢量2 i + 2 j + 7 k 绕 z 轴旋转45°后得到新的矢量 v 2 。
如果 v 2 绕 y 轴旋转90 ° 得到 v 3 ，那么 v 3 = Rot( y ,90 ° ) v 2 = Rot( y ,90 ° )Rot( z ,45 ° ) v 1 。这需要注意矩阵乘法的先后顺序，因为矩阵乘法不具备交换性质，即矩阵左乘和右乘的运动解释是不一样的。
对于固定坐标系而言，变换顺序“从右向左”；对于相对坐标系而言，变换顺序“从左向右”。
将旋转变换和平移变换整合在一起，可得到通用的齐次坐标变换矩阵。
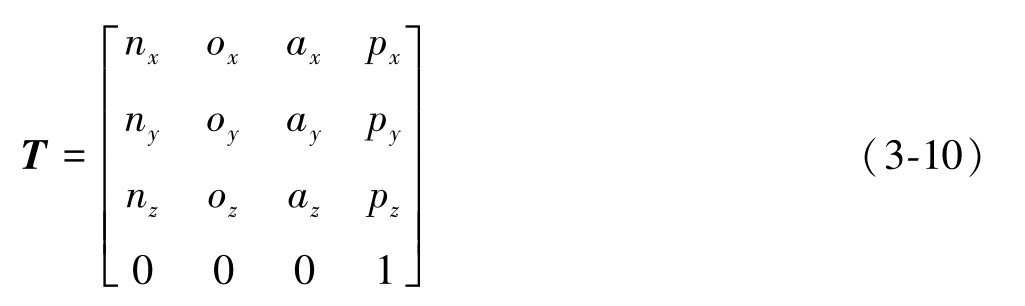
例：已知坐标系{B}的初始位姿与坐标系{A}重合，首先坐标系{B}绕坐标系{A}的 z A 轴旋转30°，再沿坐标系{A}的 x A 轴移动12单位，并沿坐标系{A}的 y A 轴移动6单位。假设点 p 在坐标系{B}的描述为 B p =[3 7 0]，求它在坐标系{A}中的描述 A p 。
解：根据式（3-6）和式（3-7），可得 A p 为
上述方法用齐次坐标描述了点 p 的位置。