




本书限定的材料均是具有线弹性属性的金属材料,但是当材料中某些部位的应力水平高于材料的屈服强度时,材料将进入非线性的塑性区间,如果卸载以后,材料某些部位产生了不同程度的永久变形,则称之为弹塑性问题,例如应力集中水平高于材料屈服强度的区域;如果卸载以后材料没有遗留任何弹性变形或仅存有塑性变形,则称之为完全塑性问题,例如车辆突然被高速碰撞后某个钢管被压缩为折叠管。本节只讨论这两类问题的基本方程与求解过程。
材料由弹性阶段进入弹塑性阶段后,3.1节与3.2节提到的物理方程已经不能用了,因为弹性阶段用到的胡克定律只是本构方程或本构关系的一种。而本构关系是反映物理性质的宏观模型,是力学中用到的物理定律。在固体力学中,本构关系多用于描述应力与应变的函数关系。
材料弹塑性的本构关系有不同的表示方式,这取决于材料本构关系用哪一种函数来表达应力与应变之间的关系,而不同的材料本构关系定义了不同的弹塑性模型,下面将逐一讨论它们的本构关系,它也构成了问题的基本方程。
1.理想弹塑性的本构关系
理想弹塑性的本构关系如图3-6所示。如果材料屈服后应变强化效应并不明显,则可以将塑性段简化为一水平线,材料在经弹性变形阶段之后就进入塑性状态,塑性变形在屈服应力 σ y 作用下可无约束发展,是真实塑性段的扩大后延。理想弹塑性模型适用于材料变形很小,而且应变强化效应不显著的情况,它在工程结构中有大量应用。
2.弹线性强化的本构关系
材料在塑性阶段应变强化效应显著的情况下,理想弹塑性模型不再适用,这时需要参考材料的拉伸实验数据来确定本构模型,通常用简单的线性函数来表征它的应变强化效应。强化以后不同的杨氏模量由不同的材料实验数据确定,弹线性强化的本构关系又称为双线性关系,如图3-7所示。
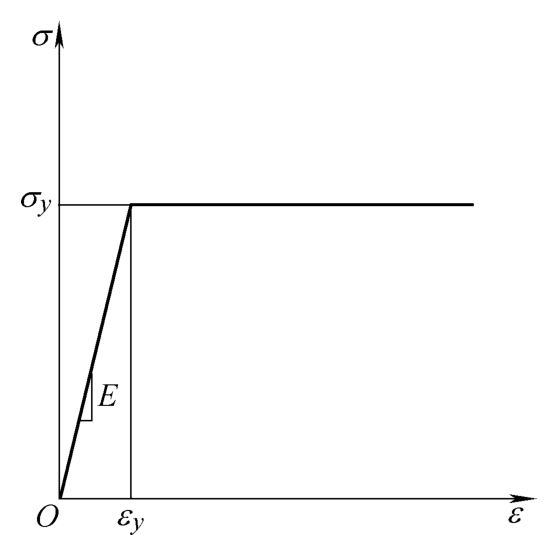
图3-6 理想弹塑性的本构关系
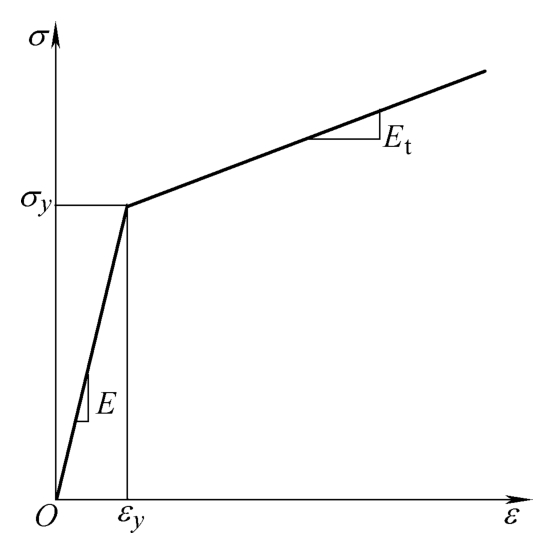
图3-7 弹线性强化的本构关系
3.弹-幂次强化模型的本构关系
这种模型中保留了材料的弹性段,塑性段采用幂次强化,强化指数来自于实验数据的统计。弹-幂次强化模型的本构关系如图3-8所示。
4.理想刚塑性的本构关系
当材料用于结构能量吸收时,材料将产生塑性大变形,且塑性变形显著大于弹性变形,使得分析过程中可以忽略弹性变形,即认为材料的应力在达到屈服强度 σ y 时就进入塑性流动状态,而材料应力小于 σ y 时为刚性状态。根据不同材料应变强化效应的不同,采用了不同的函数来表征其塑性行为,因此衍生了不同的本构模型,例如理想刚塑性模型、刚线性强化模型、刚幂次强化模型,其中理想刚塑性本构模型在薄壁管件压溃载荷的理论预测中被广泛应用。
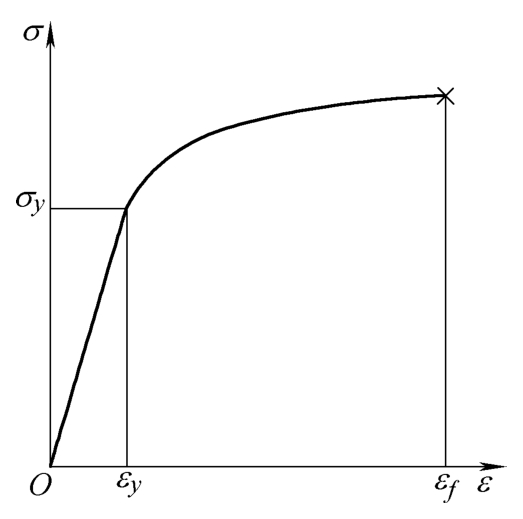
图3-8 弹-幂次强化模型的本构关系
当加载以后材料某些区域的应力应变表现为非线性关系时,其刚度矩阵不再是与位移向量无关的常量矩阵,因此基于最小势能原理推导出来的以节点位移为未知量的平衡方程将不可能直接求解。在非线性方程组的解法上,参考文献 [13,14]给出了许多方法,其中N-R法(Newdon-Raphson法的简写)是工程上常用的mN-R法的基础。它利用数学上的泰勒(Tay-lar)级数展开法,在当前位移点上将原刚度矩阵展开且仅保留一阶线性项,这相当于在当前点上用切线刚度矩阵近似替代原问题的刚度矩阵后求解,求解后获得新的位移点,然后在新的点上再用新的切线刚度矩阵替代求解,直到收敛为止,可见这是一个非线性问题被一系列线性问题替代的过程。针对N-R法每次都要更新切线刚度矩阵而导致计算工作量大的问题,又提出了修正的N-R法,即mN-R法,即它每次只用初始切线刚度矩阵求解。图3-9给出了N-R法求解过程的几何解释,如果不更新图中的切线刚度,就是mN-R法的几何解释。
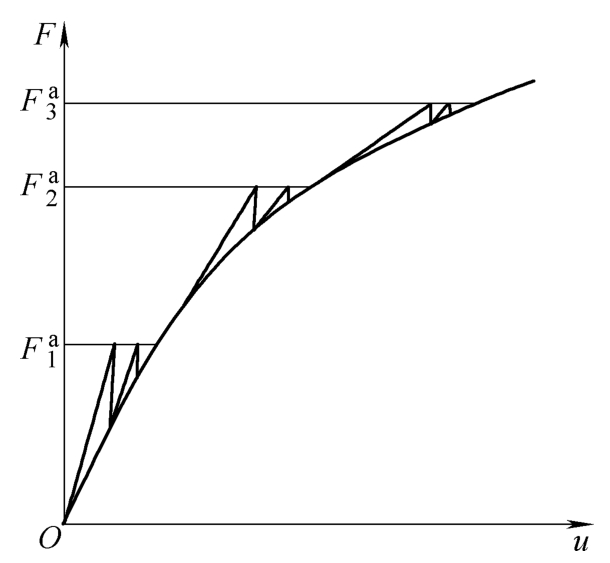
图3-9 N-R法增量迭代过程的几何解释
在数值分析的过程中,首先将载荷分为若干个增量步;然后在每一个载荷增量步中使用N-R或mN-R法,直到该载荷增量步结束。关于载荷增量步的自动选择等,参考文献 [13] 中有详细讨论,这里不再重复。
上述内容表明,材料弹塑性问题的数据链本身并不复杂,而材料本构关系的恰当选择才是工程应用中最需要关注的。
在冲击载荷工况下材料有时处于完全塑性变形状态,例如,轨道车辆的突然碰撞就属于这一状态。由于轨道车辆结构有限元模型自由度数量多,如果使用N-R方法进行隐式求解,计算量将迅速增加,因此工程上常采用中心差分法之类的显式求解。显式求解是对时间域进行差分处理后而直接求解,它不需要对刚度矩阵进行求逆运算,所有的非线性问题(包括接触)都被包含在内力矢量中,因此内力计算是主要计算量。显式求解不存在迭代和收敛问题,求解的最小时间步长取决于最小单元的尺寸。
采用显式积分按照多个时间步长进行求解,对应到每一时间步长中都需要计算屈服函数,进而判断材料是处于弹性状态还是塑性状态,然后利用本构积分算法在基于 t n 时刻的状态量来计算 t n +1 时刻的状态量,最终完成应力、应变等参量的更新。
弹塑性问题的应力更新计算流程是:计算单元切线刚度矩阵→计算单元应变→根据弹塑性材料本构模型计算单元应力,计算并判定屈服函数是否收敛→如果不收敛,进行塑性修正(即更新塑性参数增量、偏应力增量、塑性应变增量、塑性应变、塑性应力)→计算屈服强度比例系数→应力点返回屈服面。这一流程确定了数据链条的形成过程。