




理论上,任何一个结构都可以视为三维结构,但是在工程上只有当一个结构的三个坐标方向的尺度不是相差很大时才归类为空间三维结构,例如车辆牵引车钩中的铸件,柴油发动机的机体,增压器的涡轮等,它们都属于空间三维结构,图3-2给出了两个三维实例。

图3-2 机械零件的三维几何
类似于二维问题,三维问题的力学模型是由三部分组成:静力平衡方程、几何方程、物理方程。
1.静力平衡方程
图3-3是参考文献 [12] 给出的空间结构中的一个微小六面体隔离体,以及这个隔离体上的应力变化示意。
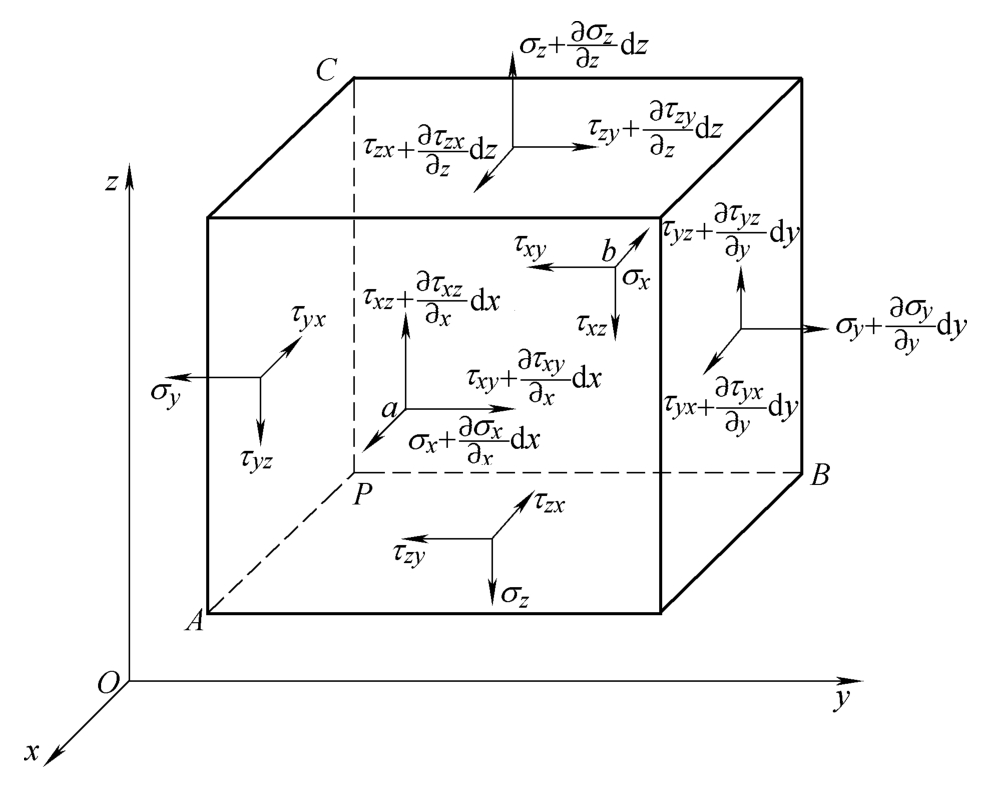
图3-3 微小六面体的应力变化关系示意
取每一点的应力状态为未知量,那么根据力的平衡条件,就有一组偏微分方程与之对应,即纳维叶方程
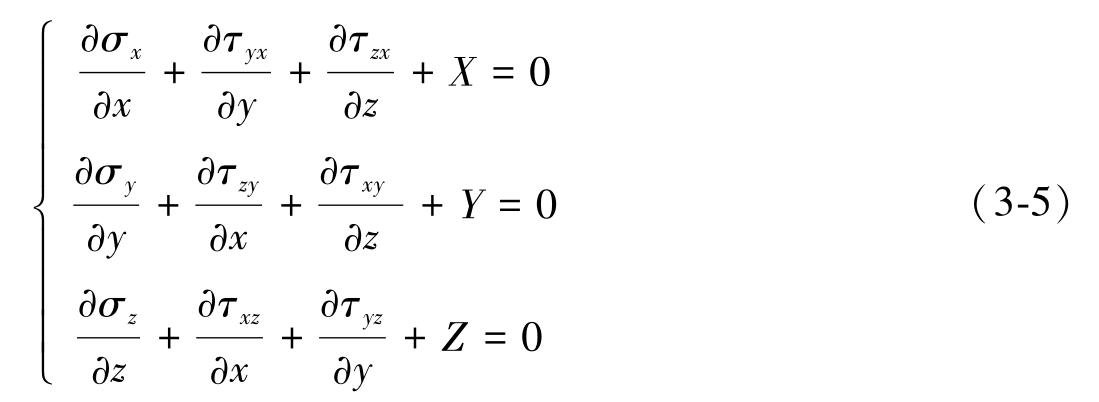
方程中 X 、 Y 、 Z 是体力,其余未知应力分量定义参见图3-3。式(3-5)的物理意义是:在任何一个坐标方向上,作为内力的体力控制了应力分量的变化,且应力分量的变化是协调的。式(3-5)虽然形式简洁但是不能被直接求解,因为未知的应力分量数多于方程数而需要补充应变和位移的关系。
2.几何方程
同样以图3-3所示的微小六面体为参考,在外力作用下将发生微小形变。当处于平衡状态时,应变和位移的几何关系将满足一个方程,即几何方程
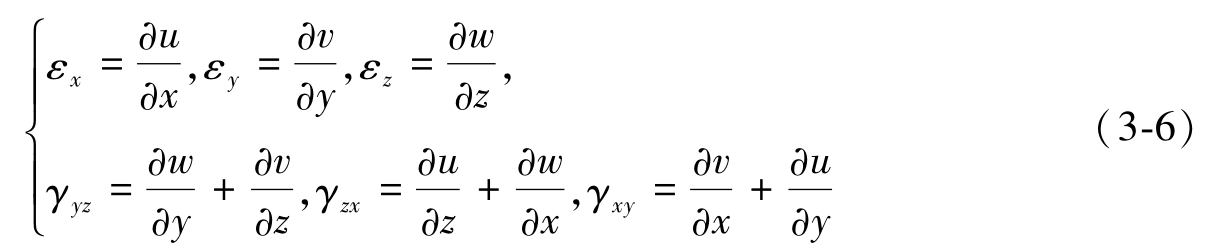
几何方程的物理意义是:如果以位移分量为未知量,那么应变分量由位移分量的偏导数控制。注意,这里的偏导数代表位移的梯度,在处理工程结构时关注位移梯度很有必要,因为它关系到应力集中的程度。
3.物理方程
在完全弹性的各向同性体内应变分量与应力分量之间的关系很简单,即服从与式(3-3)类似的广义胡克定律:给定材料的物理常数以后,应力分量与应变分量之间的关系是明确的。将广义胡克定律逆向推演,就得到了方程
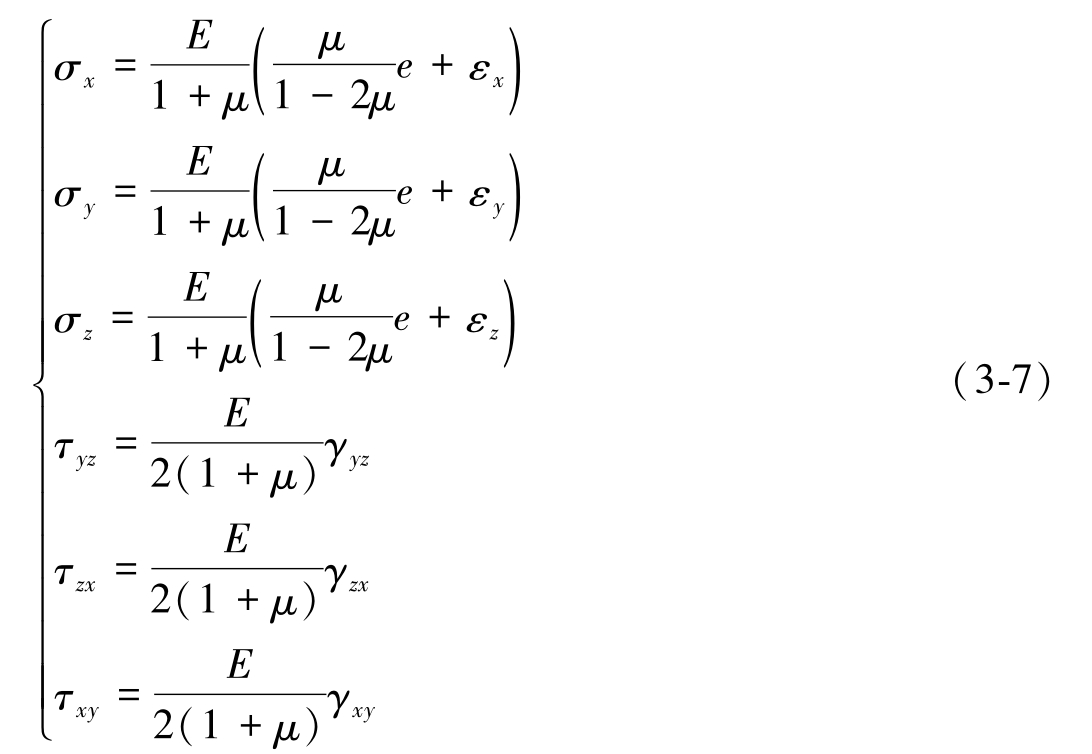
式中, e =ε x +ε y +ε z 是体积应变。
将式(3-6)带入式(3-7),再代入式(3-5)中,采用记号
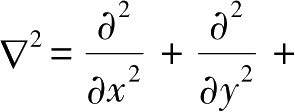
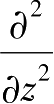 ,于是得到
,于是得到
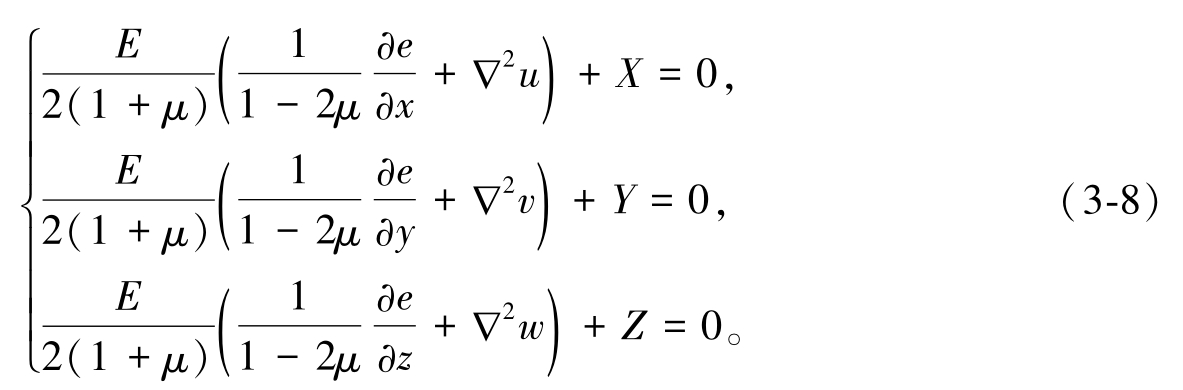
这是用位移分量表示的平衡方程,或者按位移求解空间问题时的微分方程,即拉密方程。
与二维问题类似,可以得到以位移为基本未知量的、以微分形式表示的平衡方程及所有边界条件,如果能从这个微分方程获得位移解,那么就可以按照类似的数据链获得应变与应力。
与二维问题一样,位移是数据链条的前端,因此将来的建模过程中要确保位移解及位移梯度的可靠性。因为它直接影响数据链后端的应变与应力的可靠性,因此在建模过程中如何简化结构细节,如何等效替代等操作,都应当服从于位移解的可靠性。