




固溶体(solid solution),它的英文名词直接的意思是“固体溶液”,中文译成“固溶体”很恰当。因为“固体溶液”和“固溶体”是有区别的。“固溶体”,不但是一个均匀的单相合金,还得有它自己确定的有序晶体结构,不是像溶液那样是两个组元无序混溶的。只有玻璃态的固体才算得是真正的固体溶液。
两个组元在不同的比例下都能完全“固溶”,称生成了连续固溶体。连续固溶体有确定的晶体结构,在确定的晶格节点上,均匀分布着混合的两种组元的原子。A和B能否互溶形成连续固溶体,必须满足一些条件:
1)A和B具有相同,至少极为接近的晶格类型,否则难以形成固溶体的共同晶格。
2)A和B的原子半径(或者说原子体积大小)必须相近,否则就会破坏共同的晶格。
3)A和B的化学性质也要相近,否则组元间会引起化学反应,生成新化合物或中间相,从而破坏固溶体的连续。
组元间能生成这样连续固溶体的体系,在元素周期表上多半都是处在上下、左右邻近位置的两个元素。因为相邻位置这两个元素的物理和化学性质最相近,容易满足上面所述生成连续固溶体的三个条件。相图中组元A和组元B生成了连续固溶体时,常用“(A,B)”来表示。
组元A和B之间生成的连续固溶体有三种类型,如图3-6a、b和c所示。图3-6a表示生成的是均匀的连续固溶体, l—s 线是结线,表示平衡着的液相和固溶体相的温度和组成。图3-6b和c分别是具有最低极值和最高极值熔化温度的固溶体。图中上侧的粗线是液相限;下侧的细线是固相限。
是什么原因使得生成的连续固溶体会形成图3-6a、b、c三种不同的类型?这其中反映了两个组元的配合程度,也就是符合上述三条件的程度。
对图3-6a的第一种固溶体而言,构成这类的固溶体的两个组元条件有较好的“匹配”。周期表中同族紧邻的Ag-Au、Si-Ge、Mo-W、Pd-Pt以及同周期紧邻的Cu-Ni、Pd-Rh等的相图中就经常见到这样的二元系。
图3-6a这类型相图,它的液相限和固相限间的宽度往往更进一步反映两个组元匹配的程度。匹配得越好,宽度就越窄。图3-7举出Bi-Sb、Ag-Pd、Ag-Au和Ho-Er四个典型的例子。
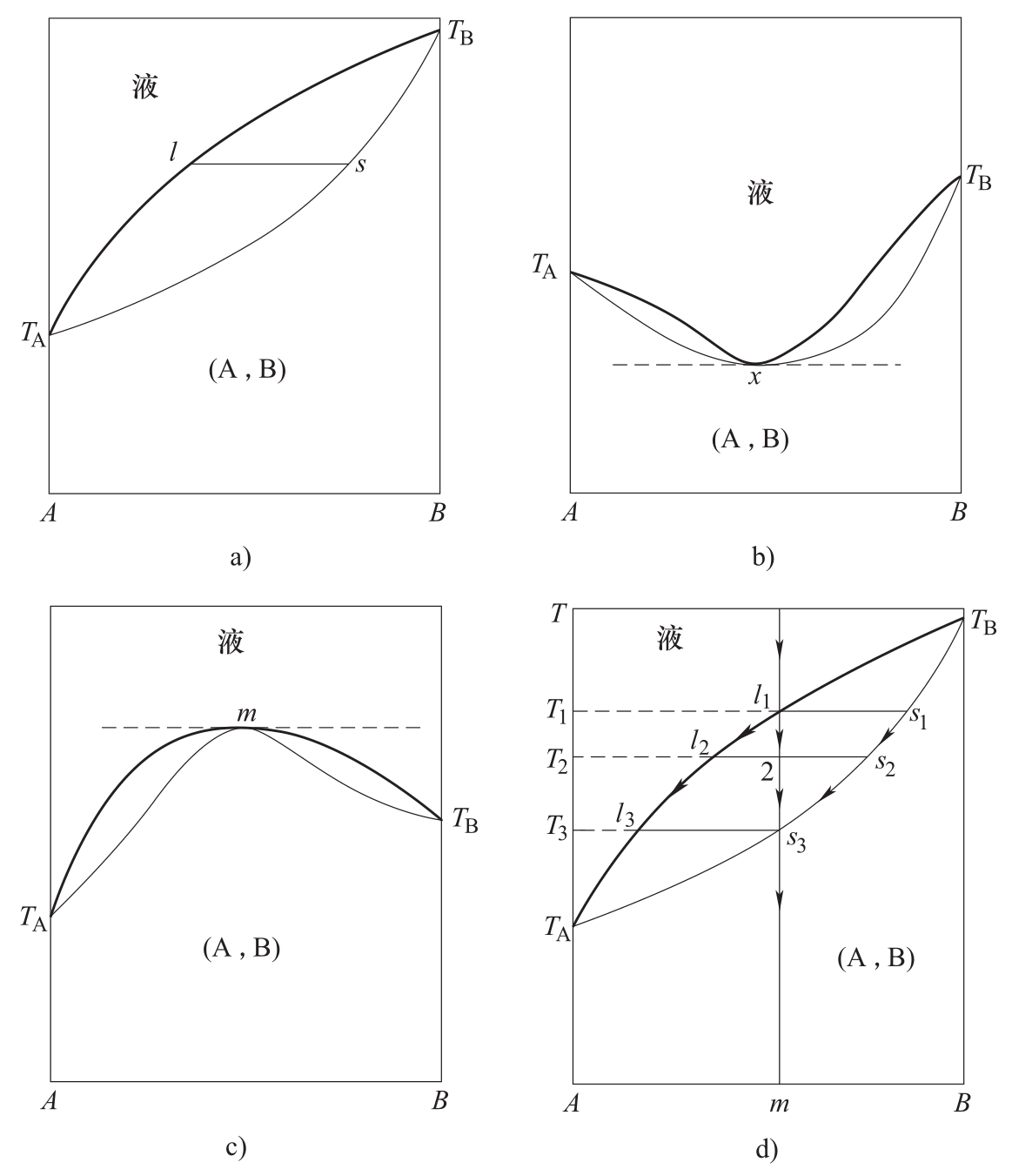
图3-6 生成连续固溶体二元系的三种类型
先看图3-7a的Bi-Sb系。在元素周期表中,Bi和Sb虽同族又都属A7的晶格结构,但Bi的原子半径为160pm,Sb的原子半径为145pm,两者原子半径相差稍大,配合度较差,它们液相限和固相限间的距离也较宽。再看图3-7b的Ag-Pd系,两个组元同属面心立方晶格并处在同一周期左右紧邻的位置,Ag的原子半径为144pm,Pd的原子半径为137pm,两者原子半径相差较小,配合度较好,液-固相限间距较窄。至于图3-7c的Ag-Au系,两个组元同属面心立方晶格,还处在同族上下紧邻的位置,Au的原子半径为144.2pm,与Ag相差甚小,两个组元配合度更好,相图中液-固相限的间距也更窄。最后看图3-7d的两个稀土元素Ho-Er系,二者的各个参数除了熔点稍有不同以外,其他的参数几乎完全相同,这类体系的液、固相限间距几乎为0,两者几近重合成了一条线,但理论上二者不应该完合重合。图3-6b是有最低极值连续固溶体的二元系。两个组元虽具有同一类型的晶格,但配合更差。例如那些虽处于周期表同族,或同周期的近邻的两个组元,当它们的原子体积(或半径)相差更大,组元间固溶的能力就会下降,表现出两个组元的液相限的温度,由于另一组元的加入而都有下降的趋势。那么形成的连续固溶体往往就会出现液相限的最低极值。这类例子屡见于同族的Cs-K、Ni-Pd、Au-Cu、As-Sb、Ba-Ca系以及不同族但在周期表中位置相邻的Cr-V、Co-Pd等体系中。上述组元的晶格结构和原子半径见附录A。
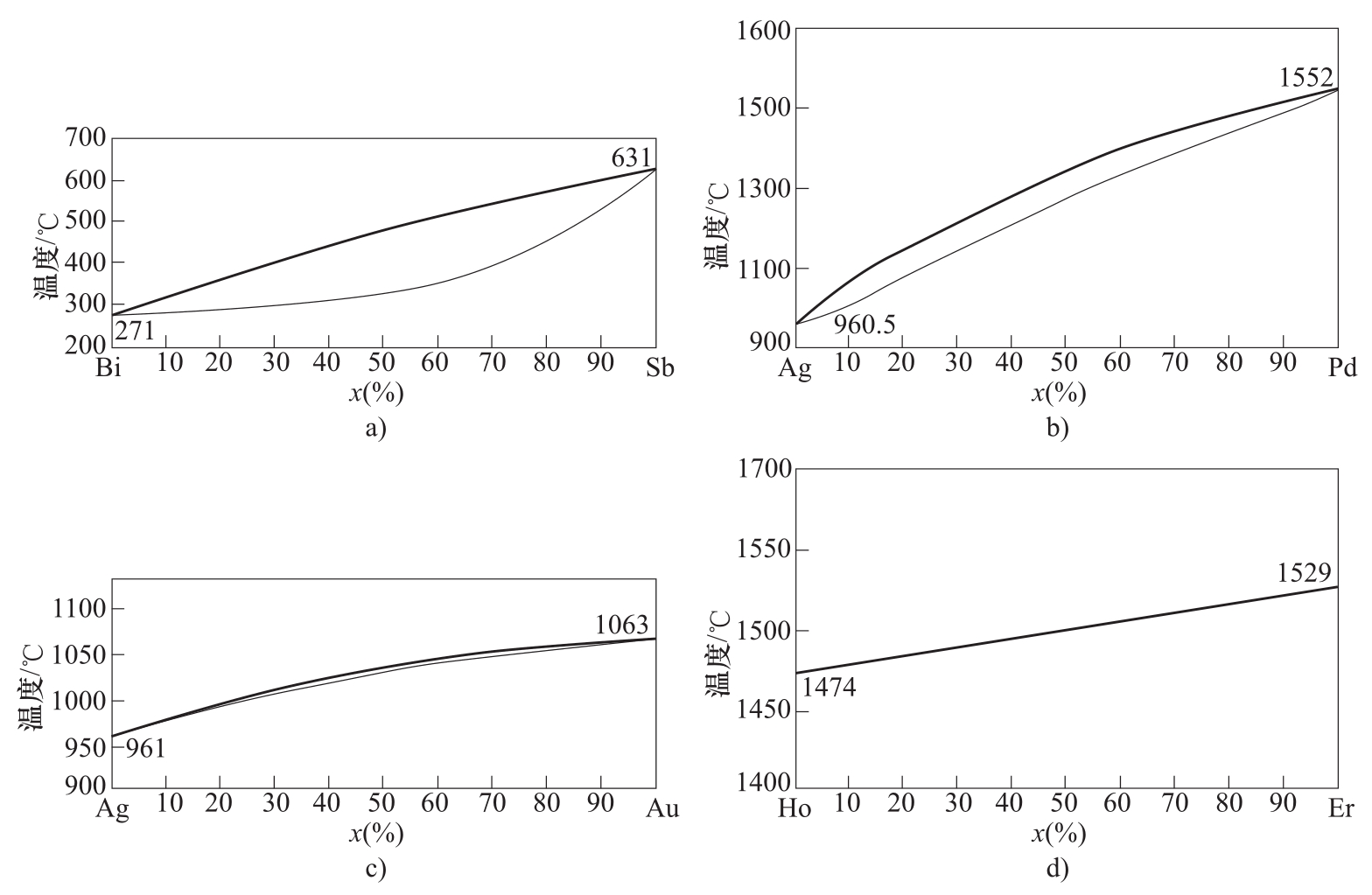
图3-7 组元间配合条件对固溶体形态的影响
图3-6c所示为具有最高极值温度的连续固溶体。这种情况如果出现,说明两个组元之间的化学性质存在较明显的差别,有部分化学反应并析出反应热的趋势,从而会抬高固、液相限的温度。实际上这种相图的典型实例出现的可能性很小。因为在连续固溶体的体系中,两个组元化学性质差别太小就不会出现极值,差别稍大,就会径直生成新相或化合物,从而破坏固溶体的连续。现实中很难存在这种恰到好处的条件。在已知的二元系中,只有Pb-Tl系算得上是唯一能接近图3-6c的实例,如图3-8所示。
在图3-8的P b-Tl系中,P b与Tl是同周期紧邻的两个元素。Tl有两个晶体构型,低温的α-Tl具有A3六方密堆的构型,在230℃转变为体心立方A2的β-Tl,而Pb的结构是A1面心立方晶格。Pb的原子半径为180pm,Tl的原子半径为170pm。可以看到α-Tl在Pb中有非常大的固溶度,一直固溶到88%。Pb在α-Tl中也有相当的固溶度,仅仅由于它们之间这点晶格和原子半径不算太大的差异,使得他们之间未能达到完全固溶而出现一片不大的分裂区。
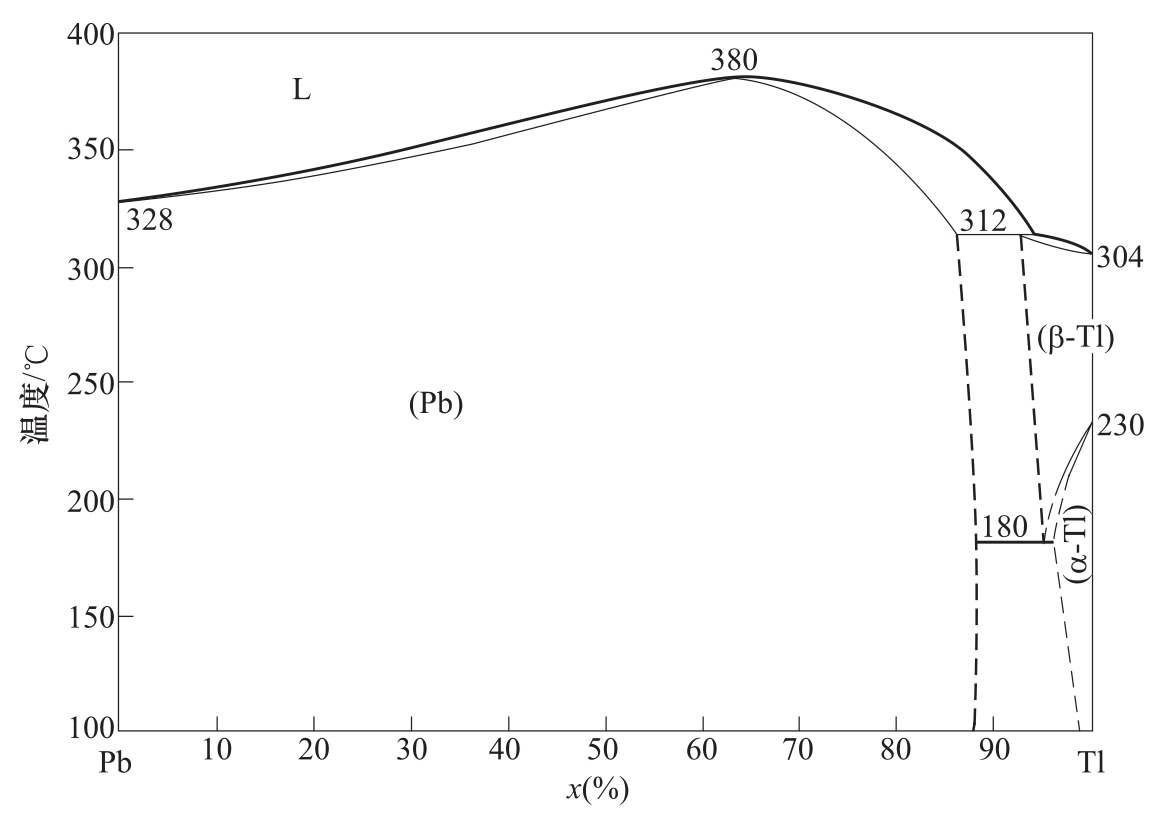
图3-8 Pb-Tl系
现在来讨论相图中连续固溶体的结晶过程(图3-6d)。图中有一个组成点为 m 的合金。温度为 T 时,它处于熔化的液相状态。降温时,液态合金的状态点就沿着过 m 点的垂线下降。当温度降到 T 1 时,合金的状态点到达 l 1 点,触到了这个体系的液相限 T A T B ,开始从液相中析出 s 1 点组成的固溶体(A,B)。温度继续下降,当状态点到达2,这时合金处在液-固平衡的两相区,液相的是 l 2 点,与之平衡的固相则变到 s 2 点。状态点2的组成可以由杠杆规则算出:2 —s 2 线段的长度相当于液相的含量,而 l 2 —2线段的长度则相当于固溶体(A,B)的含量。
温度继续下降,当状态点到达 s 3 时,液相消失,结晶过程结束。组成点为 m 的合金成为固态的(A,B)合金。
现在再来看图3-6b或c具有最低极值 x 或最高极值 m 的二元连续固溶体系。在 x 或 m 处都是处于固-液的两相平衡。其自由度由Gibbs相律算出
F (自由度)=2(组元数)+1(恒压时)-2(相数)=1
自由度不为0,因此固相限和液相限的两条曲线在此处不是相交的点而是相切的线,如图3-6b和3-6c极值处的水平相切。那种表达成自由度为0的相图描述(图3-9)是不正确的。在图3-9中,如果认定极值 x 或 m 是一个自由度为0的“点”,它只可能是一个组成确定的化合物的熔点,通过 x 或 m 点向下作一条垂线和组成坐标相交,将这条垂线当作一个“赝组元”,将原体系分割成两个赝二元系来处理,那么修改后的相图可以勉强不违背相律。但是这种新化合物或新相又能双双和两个组元生成连续固溶体的可能性几乎为0,在所有的二元系中根本不存在这样的实例。
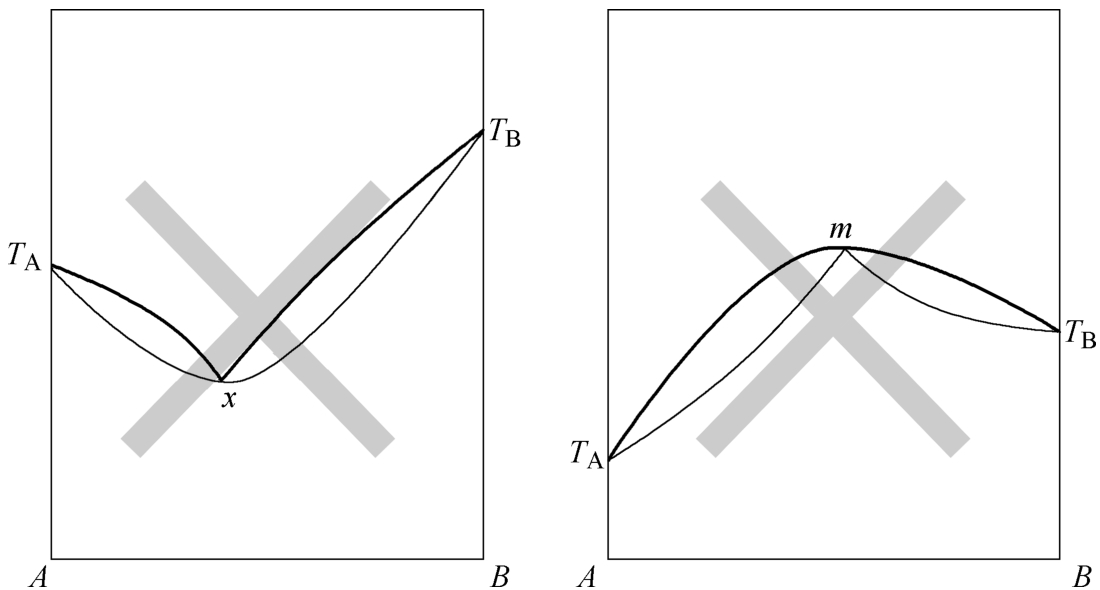
图3-9 不正确表达的两种连续固溶体相图