




寿命是指产品从诞生到失效所经历的时间长度。根据产品工作用途不同,这里的“时间”既可以是狭义上的日历时间(如年、月、日),也可以是里程、循环数等具有其他物理量纲的广义时间。
以图2.1中的四类产品为例,其用于定义寿命的时间单位分别为年、千米数、周期数、发射次数。事实上,即使是对于同一类产品,其定义寿命的“时间”也可能不止一种。例如,同样是蓄电池,当其用作电动汽车、便携式电子产品电源时,人们更关注其充放电循环寿命,而当其用作不间断电源(Uninterruptible Power Supply,UPS)时,人们更关注其存储/日历寿命。

图2.1 不同类型产品的寿命单位
工程上,由产品寿命延伸出的相关指标很多,常见的如平均寿命、分位点寿命、可靠度、剩余寿命等。实施上,这些指标之间或多或少存在一些内在关联。
同生物体寿命一样,产品寿命亦是指其从“出生”到“死亡”所经历的时间长度。显然,对于同一类产品,不同个体的自身质量或工作环境均存在差异,因而其寿命往往不同。因此,给定类型产品的寿命往往可以看作一个服从某种分布的随机变量,记为 T 。寿命预测的核心工作即是利用统计推断方法估计 T 的分布,进而对其统计特征展开分析。也就是说,如果不做特别说明,寿命是针对某一类产品而言的,它反映的是这类产品整体的质量情况。
剩余寿命是指工作到某个时刻 τ 的产品,其距离失效还能继续工作的时间长度。通常,剩余寿命是针对工作中的某个具体产品进行定义的(当然也有针对产品总体的剩余寿命概念,但本书不涉及)。由于未来情况未知,因此给定时刻 τ ,某产品剩余寿命理论上也是一个随机变量,记为 l 。同寿命预测一样,剩余寿命预测的核心工作也是利用统计推断方法估计随机变量 l 的分布,进而对其统计特征展开分析的。
寿命与剩余寿命的关系如图2.2所示。
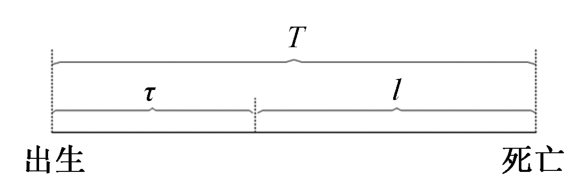
图2.2 寿命与剩余寿命的关系
寿命 T 是一个随机变量,其统计特征可由概率密度函数(Probability Density Function,PDF)或累积分布函数(Cumulative Distribution Function,CDF)描述,分别记为 f ( t )和 F ( t )。显然,有

那么,结合PDF,即可进一步定义产品的平均寿命。对于可修产品,平均寿命也称平均故障间隔时间(Mean Time between Failure,MTBF),对于不可修产品,平均寿命又称平均失效前时间(Mean Time to Failure,MTTF)。本书不考虑产品修复情况,故记平均寿命为MTTF,其计算公式为

可靠性是指产品在规定条件下、规定时间内完成规定功能的能力,可靠度是可靠性的概率度量。通俗来说,给定时刻 t ,可靠度 R ( t )是指产品在 t 时刻可以正常工作的概率,即
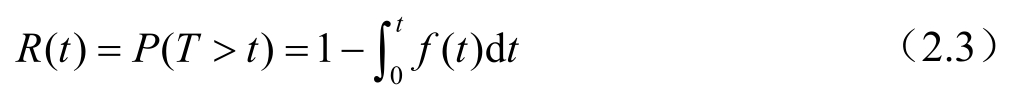
显然, R ( t )=1 -F ( t )。也就是说,不管是产品寿命的概率密度函数、累积分布函数还是可靠度函数,其都是对寿命 T 这一随机变量统计特征的刻画和描述,只不过出发视角有所不同而已。因此,可以认为,产品可靠性评估和寿命预测/评估(这里指总体寿命)本质上属于同一类工作。
需要说明的是,除式(2.2)外,平均寿命MTTF还可以用式(2.4)计算得到,即

其推导过程如下:
[ tR ( t )]′= R ( t )+ tR′ ( t )= R ( t ) -tf ( t )
于是有
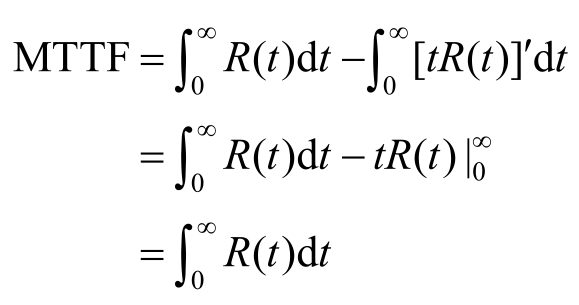
失效率 λ ( t )是可靠性工程人员关注的一项指标,其指工作到时刻 t 尚未失效的产品,在该时刻之后单位时间内发生失效的概率。于是有
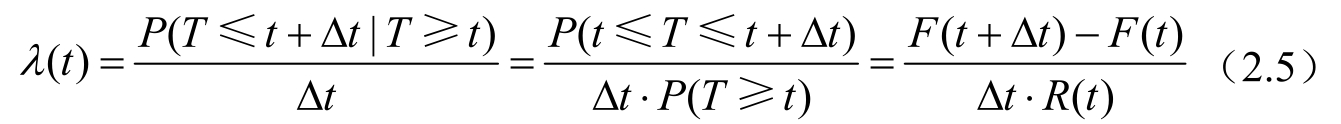
当Δ t→ 0时,得到

除平均寿命外,工程上有时还会对产品的可靠寿命(也称分位点寿命)感兴趣,其定义如下:
若

则 T q = R -1 ( q )称为产品的100 q th 分位点寿命。
经过上述分析可知,寿命和可靠度通常是针对某一类产品总体而言的,寿命分布估计和可靠性评估本质上都是对产品总体寿命统计特征的刻画,只不过其关注的统计量有所差异而已,如CDF、PDF、 R ( t )、 λ ( t )、MTTF、 T q 等,这些统计量最终都是由寿命这一随机变量的分布决定的。
剩余寿命通常是针对某类产品总体中的某个个体产品而言的,剩余寿命预测是对个体在给定时刻剩余寿命这一随机变量分布的估计,工程上常用其PDF、平均值、中位值、置信区间等统计量进行刻画。剩余寿命预测方法包括数据驱动方法、失效物理方法、融合方法等。数据驱动方法又可分为机器学习方法和性能退化方法,本书主要关注后者。虽然近年来以机器学习为代表的“黑箱模型”在剩余寿命预测中取得了一些成果,但由于其物理可解释性差,需要一定数量失效数据作为训练样本,且难以对剩余寿命的不确定性进行度量,应用范围受到一定限制 [132] 。在性能退化方法框架下,剩余寿命预测主要包括三方面工作 [69] :一是建立描述产品性能参数随时间变化的退化模型;二是结合现场监测数据实时更新模型参数,修正模型精度;三是根据失效阈值推断剩余寿命分布。剩余寿命预测方法体系及研究思路如图2.3所示。
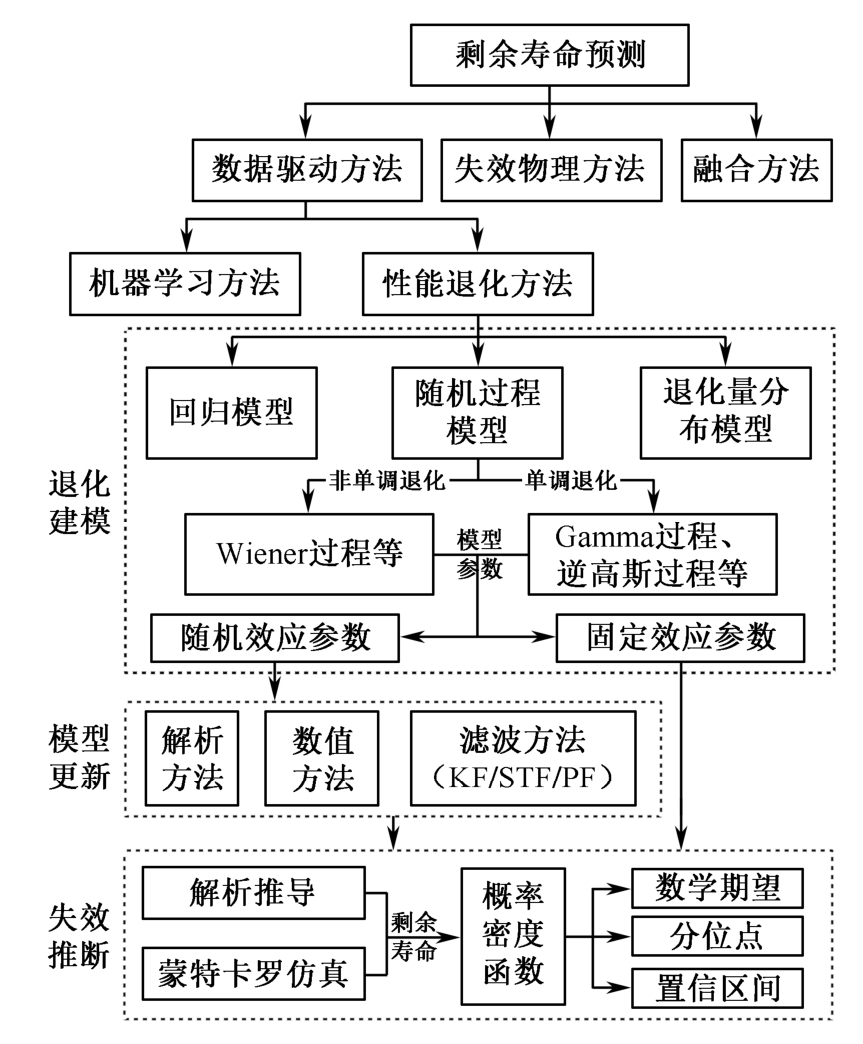
图2.3 剩余寿命预测方法体系及研究思路
总结发现,寿命和可靠性多是针对某一类产品总体而言的,剩余寿命多是针对某个产品个体而言的。也就是说,可以将产品寿命预测分为总体寿命预测和个体寿命预测两大类,前者主要解决总体寿命分布估计或可靠性评估问题(本质上为一类问题),后者重点解决剩余寿命预测问题。