第三节
逆矩阵

一、逆矩阵的定义

在数的运算中，若数 a ≠0，则存在 a ^-1 ，使 aa ^-1 = a ^-1 a =1，于是，称 a ^-1 为 a 的逆元素。

而在矩阵乘法中，单位矩阵 E 类似于1在数的乘法运算中的作用，由此给出矩阵的逆的定义。

定义2-12 对 n 阶方阵 A ，存在 n 阶方阵 B ，使

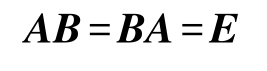
则称方阵 A 是可逆的，并把方阵 B 称为方阵 A 的逆矩阵。

显然，若 B 是 A 的逆矩阵，则 A 也是 B 的逆矩阵，即 A 与 B 是互逆的。

事实上，若矩阵 A 是可逆的，设 B 、 C 都为 A 的逆矩阵，得到

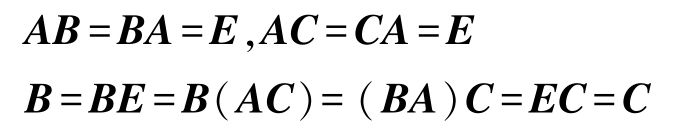
则 A 的逆矩阵唯一，记为 A ^-1 。

二、可逆的充要条件

一个 n 阶方阵 A 在什么条件下可逆？若 A 可逆，怎样去求 A ^-1 ？

下面来探讨一个 n 阶方阵 A 可逆的条件。设

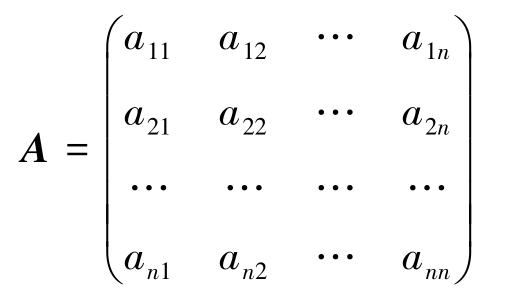
定义2-13 将矩阵 A 的行列式| A |的代数余子式 A _ij 放在相应元素位置上后所得矩阵，再取转置，构造出一个 n 阶方阵，称为 A 的伴随矩阵，简称伴随阵，记为 A ^* ，即

例2-13 求方阵 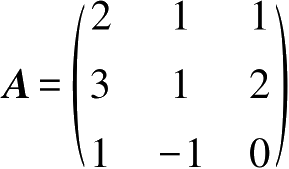的伴随矩阵。

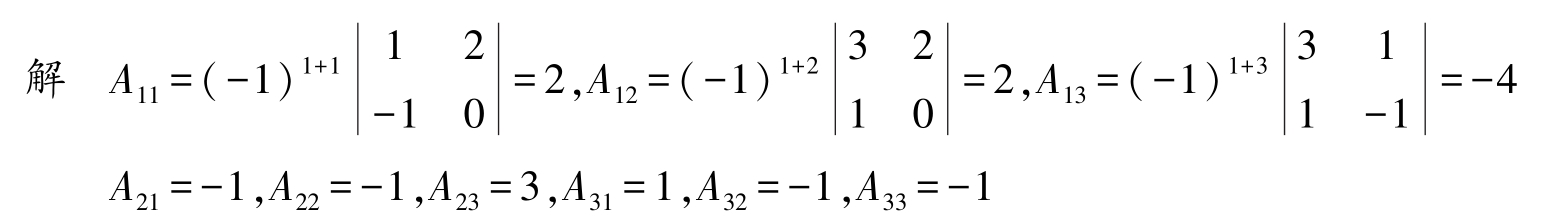
所以 A 的伴随矩阵为

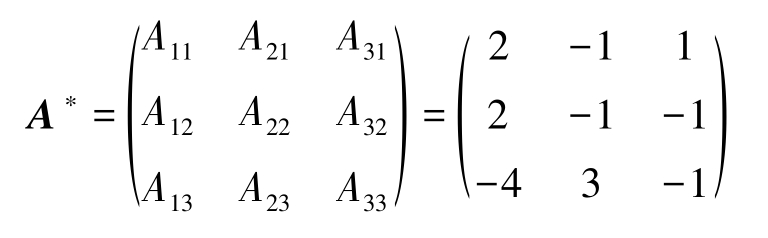
又因为

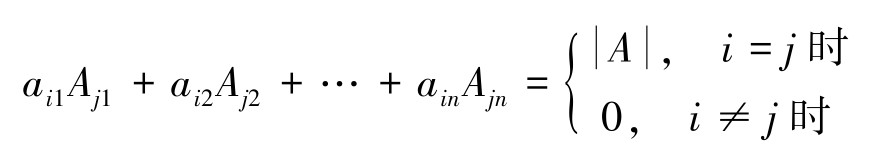
那么就有

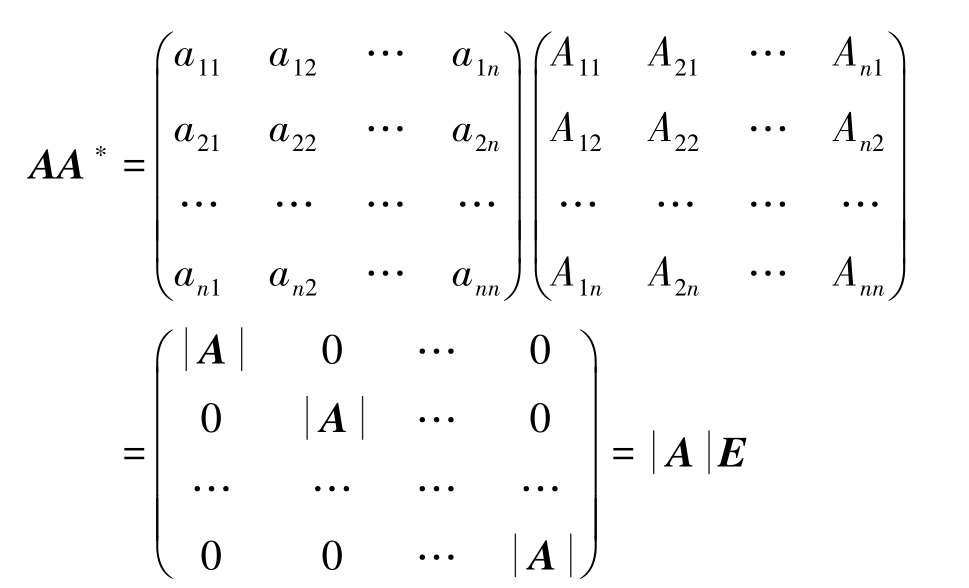
类似有 A ^* A =

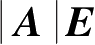
即 AA ^* = A ^* A =

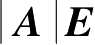
只要 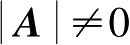，就有

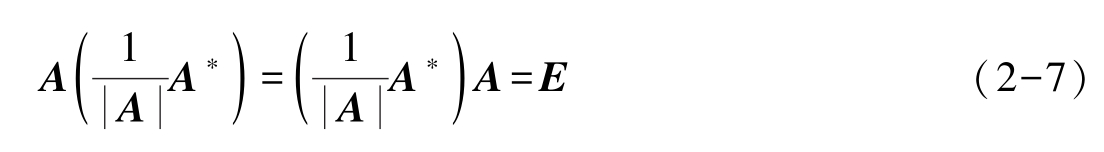
因而 A 可逆，并且有

定理2-1 n 阶方阵 A 可逆的充要条件是| A |≠0。

证明　必要性：若 A 可逆，则存在 A ^-1 使 AA ^-1 = E ，两边取行列式，

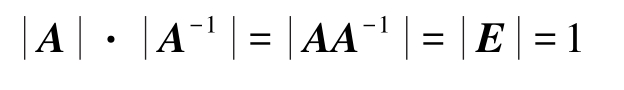
从而 。

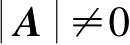充分性：若 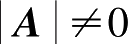，由2-7式知 A 可逆。

即，得证。

至此，既得到了方阵可逆的判别方法，又得到了一种求逆矩阵的具体方法。

定义2-14 如果 n 阶方阵 A 的行列式| A |≠0时，称 A 是非奇异矩阵，否则称 A 是奇异矩阵。

定理2-2 n 阶方阵 A 可逆的充要条件是 A 为非奇异矩阵。

定理2-3 若 AB = E （或 BA = E ），则 A ^-1 存在，且 B = A ^-1 。

证明　由| AB |=| E |=1，得| A || B |=1，故| A |≠0，由定理2-1知 A ^-1 存在，故

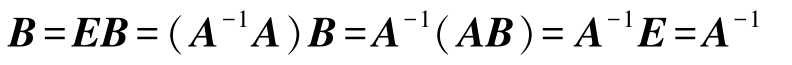
得证。

定理2-3使矩阵可逆的判定条件减弱了。

三、逆矩阵的计算

当 A 为非奇异矩阵时，可由式2-8计算逆矩阵。

例2-14 求例2-13中方阵 A 的逆矩阵。

解　| A |=2×2+1×2+1×（-4）=2≠0，故 A ^-1 存在，

再根据例2-13所得 A 的伴随矩阵，从而

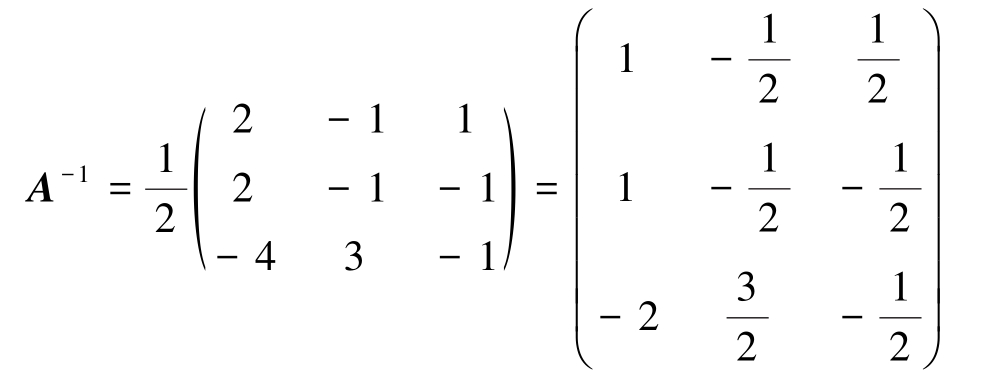
例2-15 设方阵 A 满足 A ² - A -2 E = O ，证明 A 可逆，并求 A ^-1 。

解　由 A ² - A -2 E = O 得 A ² - A =2 E ，

即 A （ A - E ）=2 E

故

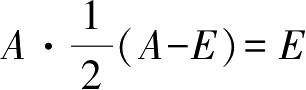
由定理2-3知 A 可逆，且 。

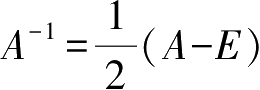在 n 元线性方程组 AX = b 中，若系数矩阵 A 是非奇异矩阵，则

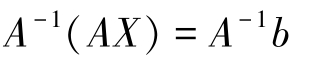
故线性方程组 AX = b 的解为

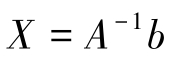
例2-16 利用逆矩阵解线性方程组。

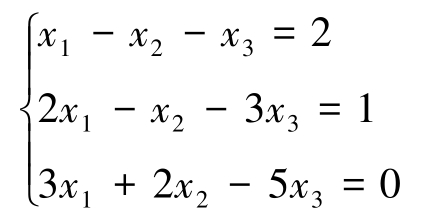
解　把线性方程组改写为矩阵方程形式，即

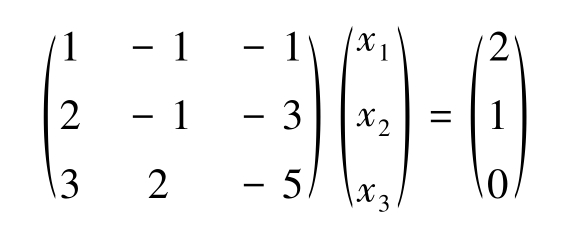
系数行列式| A |中， A ₁₁ =11， A ₁₂ =1， A ₁₃ =7，从而

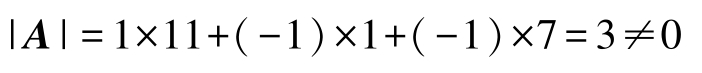
A ^-1 存在，再计算

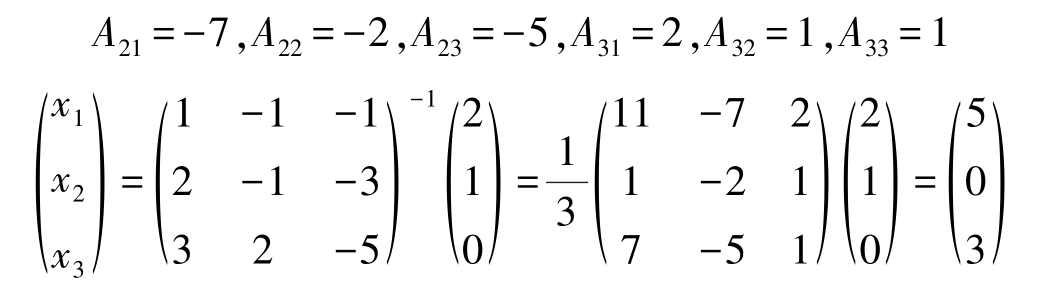
故线性方程组的解为

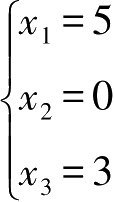
对于矩阵方程

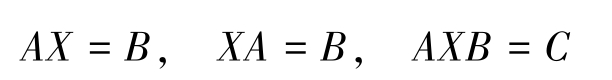
利用矩阵乘法运算和逆矩阵运算，在方程两边左乘或右乘相应矩阵的逆矩阵，可求出其解分别为

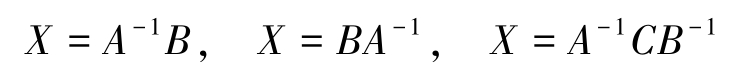
例2-17 求矩阵 X ，使其满足 AXB = C ，其中

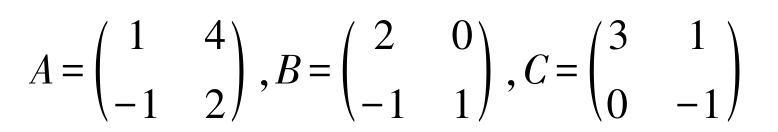
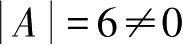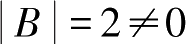解　因为 ，而 ，故 A ， B 都可逆。

由 A ^-1 AXBB ^-1 = A ^-1 CB ^-1 可以解出 X = A ^-1 CB ^-1 。

四、逆矩阵的运算性质

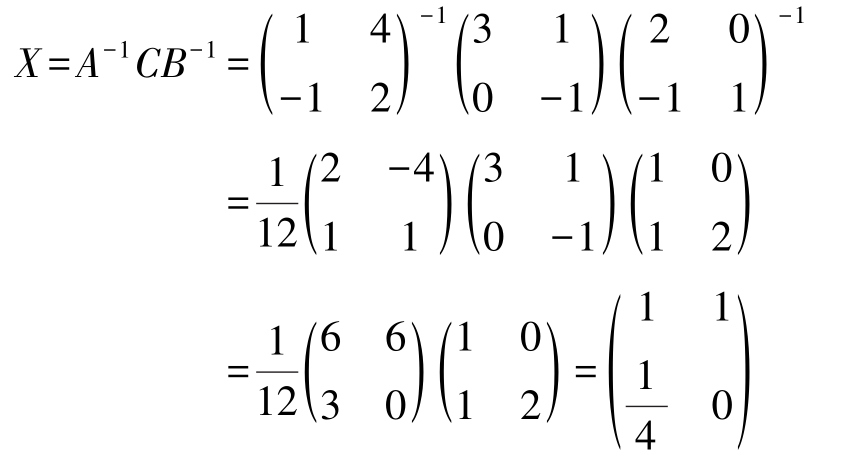
1.若矩阵 A 可逆，则 A ^-1 也可逆，且（ A ^-1 ） ^-1 = A 。

2.若矩阵 A 可逆，数 k ≠0，则 k A 也可逆，且 。

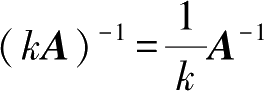3.若矩阵 A 可逆，则 A ^T 也可逆，且（ A ^T ） ^-1 =（ A ^-1 ） ^T 。

4.若矩阵 A 可逆， 。

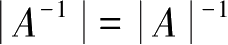5.若矩阵 A 、 B 为同阶方阵且均可逆，则 AB 也可逆，且（ AB ） ^-1 = B ^-1 A ^-1 。

证明　1.由 AA ^-1 = E ，知 A ^-1 可逆，并且 A 为 A ^-1 的逆矩阵，即（ A ^-1 ） ^-1 = A 。

2.由 AA ^-1 = E ，得到

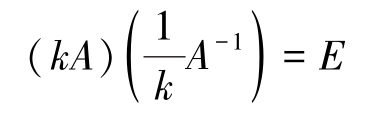
故 k A 可逆，且（ k A ） ^-1 = 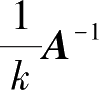，得证。

3.由 AA ^-1 = E 得到

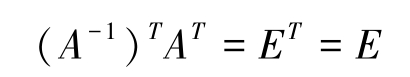
故（ A ^-1 ） ^T 是 A ^T 的逆矩阵，即（ A ^T ） ^-1 =（ A ^-1 ） ^T ，得证。

4.由 AA ^-1 = E 得到

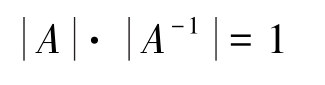
即 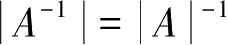，得证。

5.（ AB ）（ B ^-1 A ^-1 ）= A （ BB ^-1 ） A ^-1 = AEA ^-1 = AA ^-1 = E

故 B ^-1 A ^-1 是 AB 的逆矩阵，（ AB ） ^-1 = B ^-1 A ^-1 ，得证。

此性质可推广到有限个同阶可逆阵，即若矩阵 A ₁ ， A ₂ ，…， A _m 为同阶方阵且均可逆，则 A ₁ A ₂ … A _m 也可逆，且 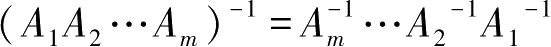。特别地，若矩阵 A 可逆，则 A ^m 也可逆，且（ A ^m ） ^-1 =（ A ^-1 ） ^m 。

练习

1.求下列矩阵的逆矩阵。

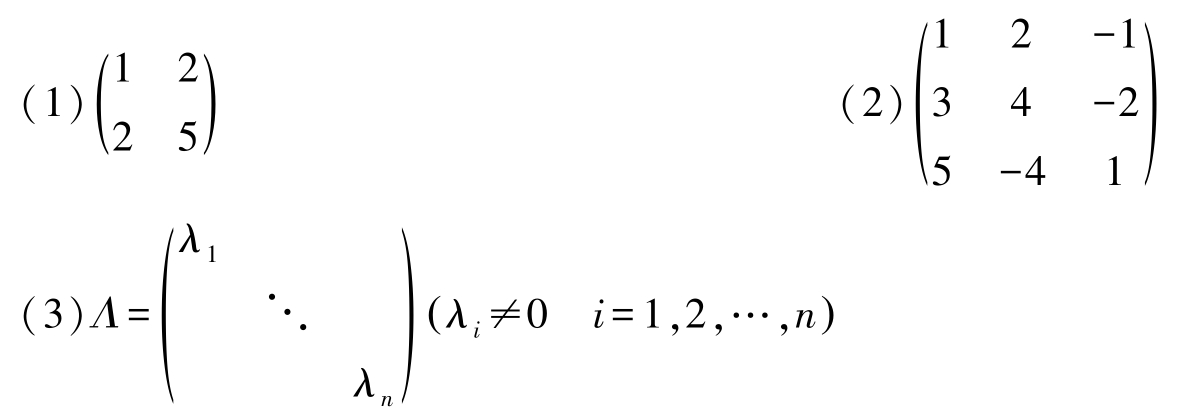
2.解矩阵方程 。

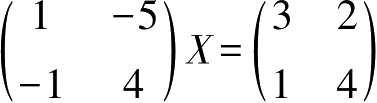3.设方阵 A 的逆 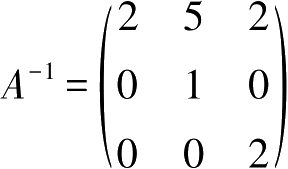，计算（2 A ） ^-1 和 。

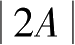4.已知线性变换

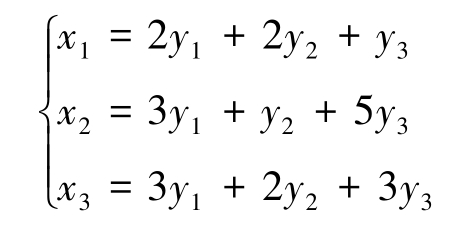
求从变量 x ₁ ， x ₂ ， x ₃ 到变量 y ₁ ， y ₂ ， y ₃ 的线性变换。

5.利用逆矩阵解线性方程组 。

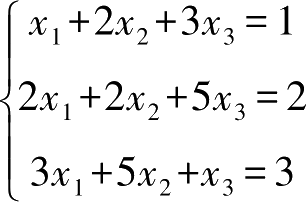6.已知

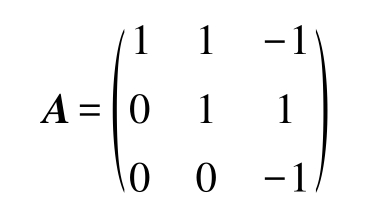
且 A ² - AB = E ，其中 E 是三阶单位矩阵，求矩阵 B 。

7.已知 AP = PB ，其中 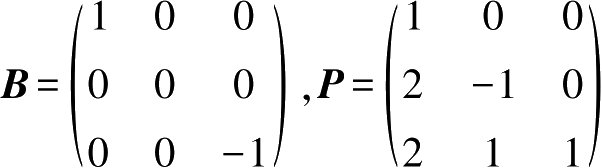，求 A 及 A ⁵ 。

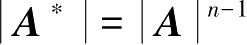8.设 A ^* 是 n 阶矩阵 A 的伴随矩阵，证明： 。 aBkFrYeZeXQpeVBltqD4MWNr5hXIgXYVAa6ymd5Uyb8tOW9uTlgnmRuAhaM3U1hP