




例2-4 若例2-1中的临床试验一共进行两批,第一批临床试验数据如矩形数表2-1所示,记为矩阵 A ;第二批调查数据得到矩阵 B ,即
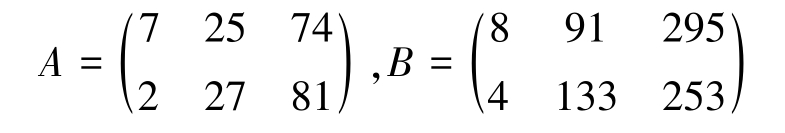
这两批数据合起来分析,能否用矩阵表示?
解 两批数据合起来,也就是把矩阵 A 、 B 对应元素相加,构成一个新矩阵 A + B ,即
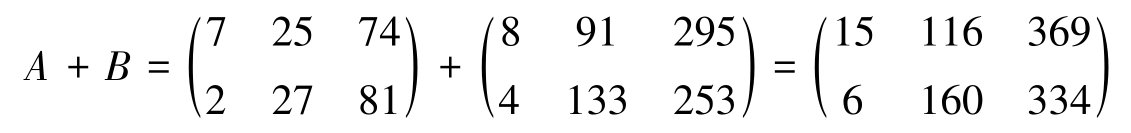
定义2-2 设 A =( a ij ) m × n 、 B =( b ij ) m × n ,则它们对应元素之和构成的矩阵 C =( a ij + b ij ) m × n 称为矩阵 A 与 B 的和,记为 C = A + B ,即
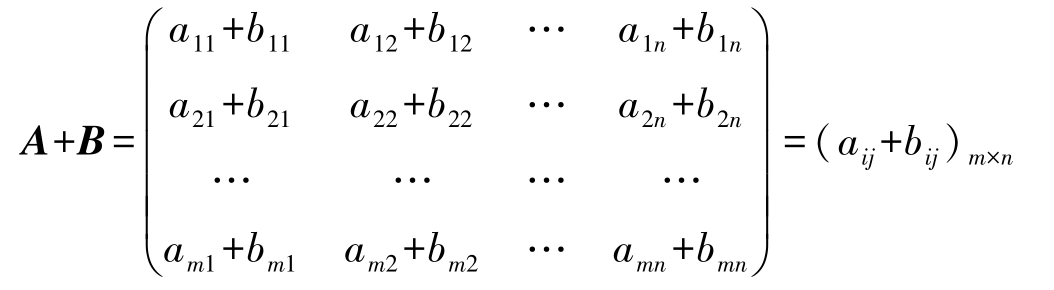
两个矩阵相加是对应元素相加,且只有同型的两个矩阵才能相加。
定义2-3 矩阵的减法为 A - B =( a ij - b ij ) m × n ,即两个矩阵相减是对应元素相减,且只有同型的两个矩阵才可以相减。
定义2-4 数 k 乘矩阵 A m × n =( a ij ) m × n 每一个元素构成的矩阵,称为数 k 与矩阵 A 的积,简称为数乘矩阵,也说成是 A 的 k 倍,记作 k A 或 A k ,即
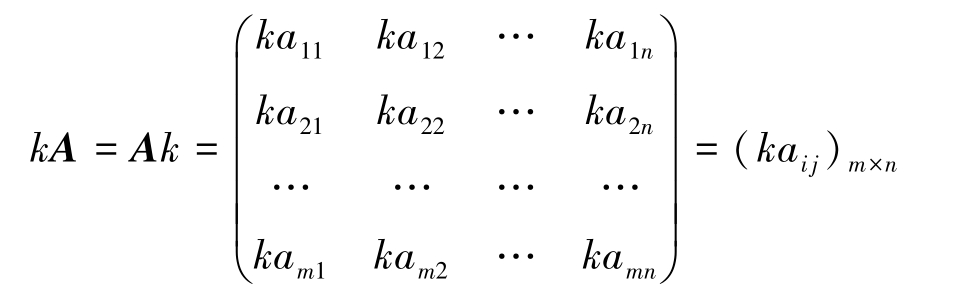
数乘矩阵是乘矩阵的每一个元素,数乘行列式是只乘行列式某一行(列)的元素。
特别地,(-1)· A =(- a ij ) m × n ,称为矩阵 A 的负矩阵,记为- A 。
矩阵的加法与数乘矩阵统称为矩阵的线性运算。
设 A 、 B 、 C 、 O 均为 m × n 矩阵, λ 、 μ 为常数, n 为正整数,则矩阵的线性运算有以下规律。

特别地
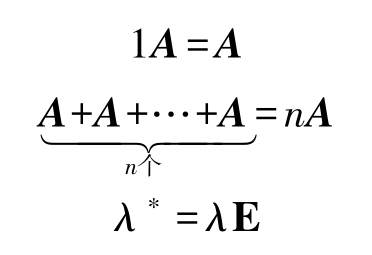
零矩阵的特性:
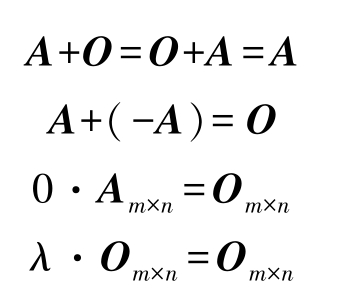
例2-5
已知3
A
+2
B
=
C
,其中
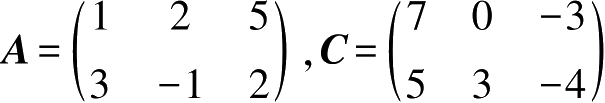 ,求
B
。
,求
B
。
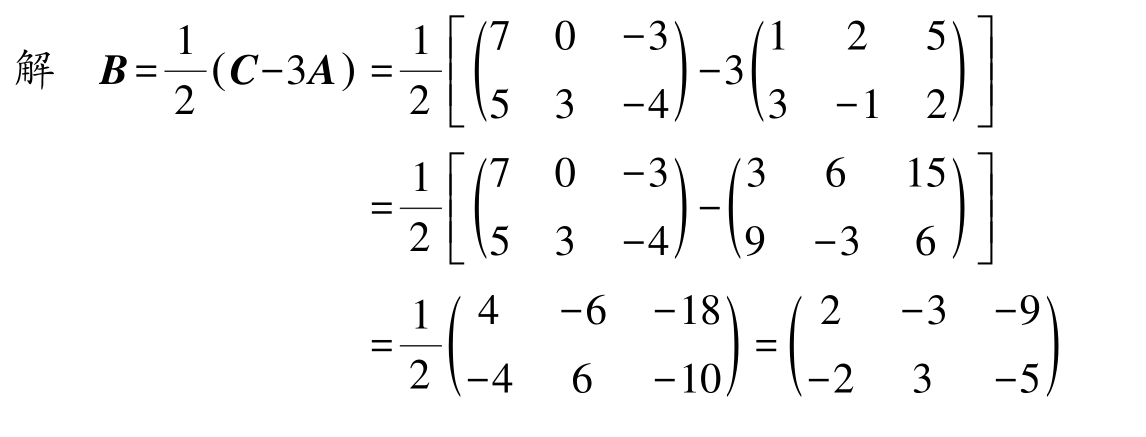
引例 已知从 x 1 、 x 2 、 x 3 到 y 1 、 y 2 的线性变换
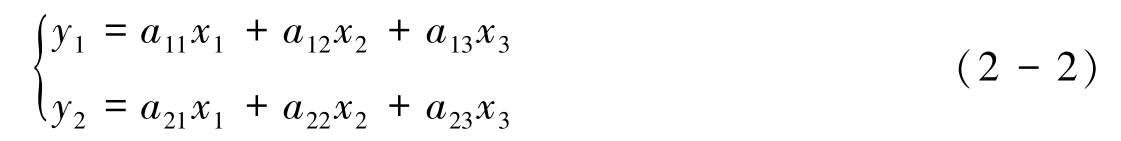
从 z 1 、 z 2 到 x 1 、 x 2 、 x 3 的线性变换

求从 z 1 、 z 2 到 y 1 、 y 2 的线性变换。
解 把(2-3)的各式代入(2-2)的各式,得到
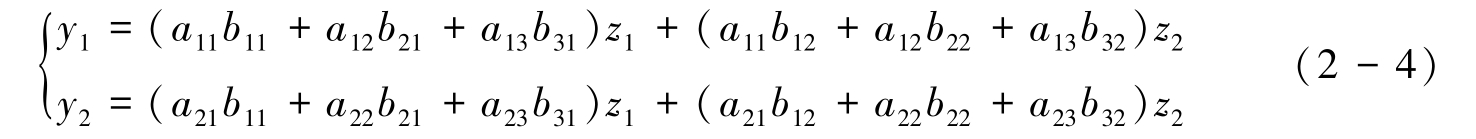
称线性变换(2-4)是线性变换(2-2)与(2-3)的乘积变换,称线性变换(2-4)对应的矩阵是线性变换(2-2)与(2-3)对应矩阵的乘积,即
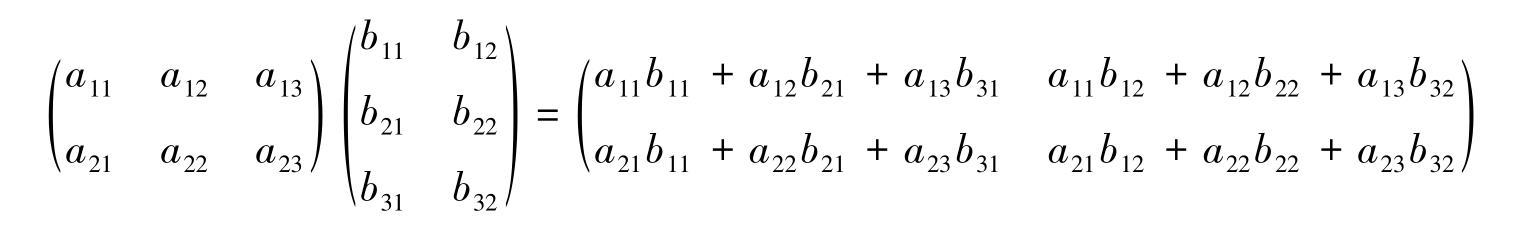
等式的左边,第一个矩阵的列数等于第二个矩阵的行数。等式的右边,乘积阵的第 i 行、第 j 列交叉处的元素,是左边第一个矩阵的第 i 行元素与第二个矩阵的第 j 列对应元素相乘再相加而得。
例2-6 某单位出现两名流行病患者,甲组3名工作人员中,第 j 名人员与第 i 名患者近期内接触情况用 a ij 表示,有临床意义上的接触记为1,否则记为0,构成矩阵 A ,设为
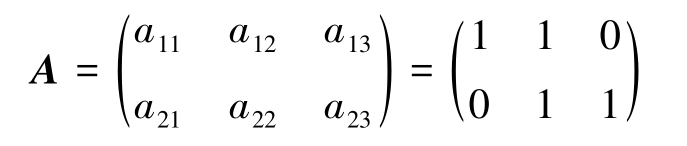
乙组2名工作人员与患者虽无直接接触,但与甲组工作人员联系密切,接触情况构成矩阵 B ,设为
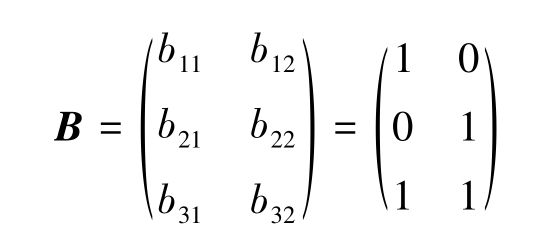
研究乙组人员通过甲组人员与患者间接接触的情况。
解 乙组人员1通过甲组人员与患者1间接接触1次,即
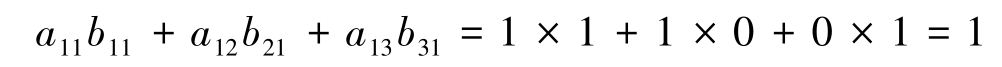
类似计算乙组人员1与患者2间接接触次数,乙组人员2与患者1、2间接接触次数,构成矩阵 C ,即
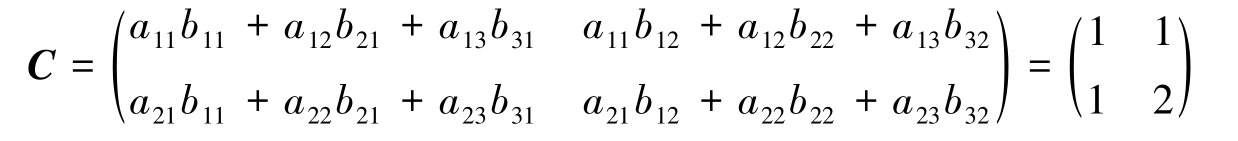
一般地,我们有矩阵乘法的定义。
定义2-5 设矩阵 A =( a ik ) m × s 、 B =( b kj ) s × n ,规定矩阵 A 与 B 的乘积 AB 是矩阵 C =( c ij ) m × n ,其中, c ij 等于 A 的第 i 行元素与 B 的第 j 列元素对应乘积之和,即
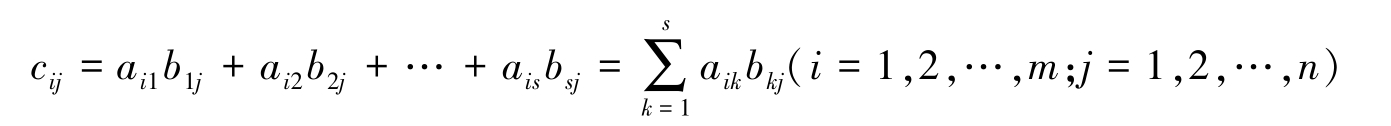
矩阵乘法必须满足的条件:只有当第一个矩阵的列数等于第二个矩阵的行数时,两个矩阵才能相乘。
例2-7
已知
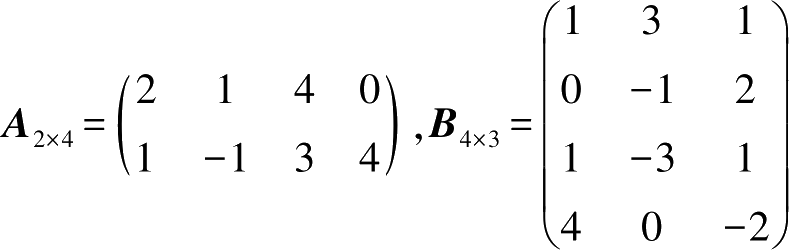
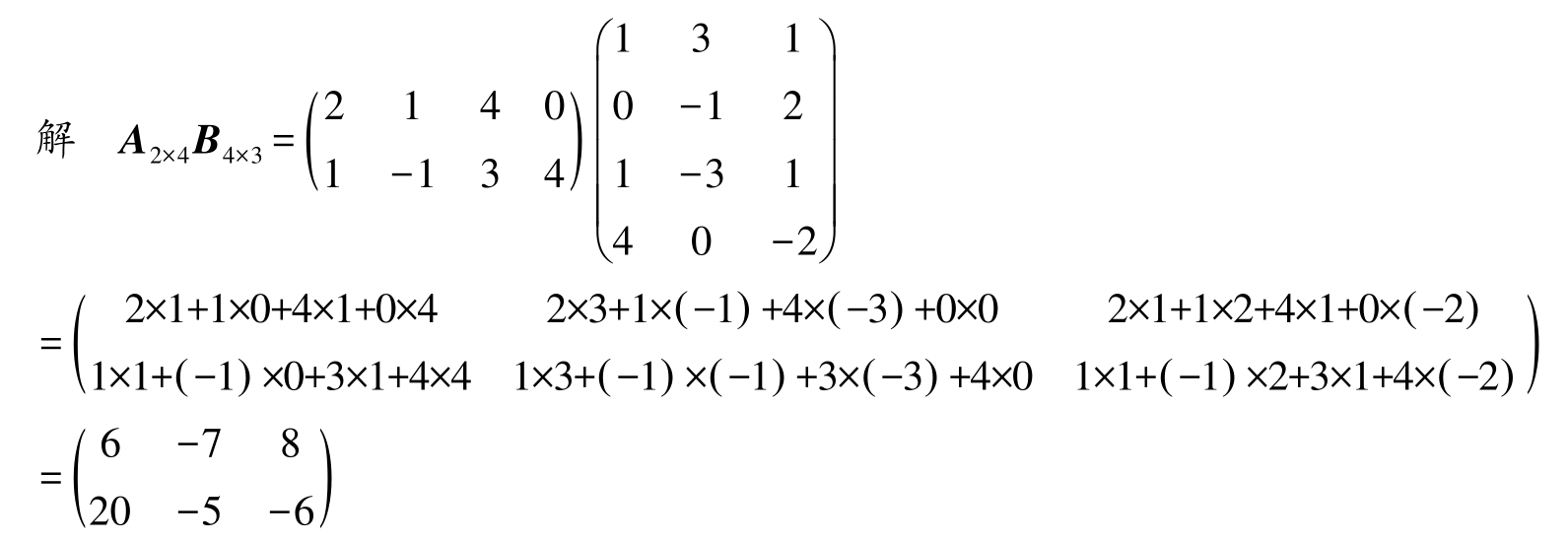
但是, B 4×3 A 2×4 无意义。注: AB 有意义, BA 未必有意义。
由此可知,在矩阵的乘法中,必须注意矩阵相乘的顺序。通常把 AB 说成“ A 左乘 B ”或“ B 右乘 A ”。即使 AB 与 BA 都有意义,它们也未必同型。例如, A 2×3 B 3×2 是2×2型矩阵, B 3×2 A 2×3 是3×3型矩阵。此外,即使 AB 与 BA 都有意义且同型,这两个乘积也未必相等。
例2-8 求矩阵 AB 和 BA 。
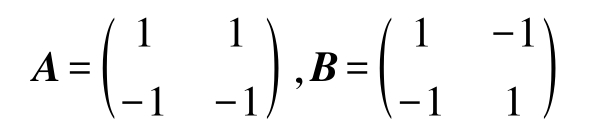
解 AB 和 BA 符合矩阵乘法的条件,计算得到
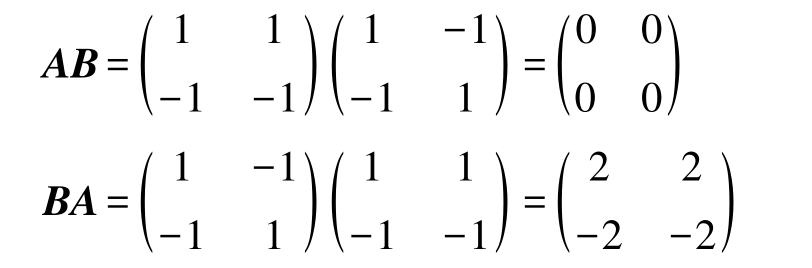
由例2-8可以看出,矩阵乘法运算一般情况下不满足交换律,即 AB ≠ BA 。
定义2-6 若 AB = BA ,则称矩阵 A 与 B 可交换。
由例2-8还可以看出,矩阵 A ≠ O , B ≠ O ,但却可能有 AB = O 。这就说明:两个矩阵 A 、 B 满足 AB = O ,得不出 A 、 B 至少有一个是零矩阵的结论。此外,矩阵乘法运算也不满足消去律,即若 AC = BC , C ≠ O ,但不一定有 A = B 。
在运算可行时,矩阵乘法满足下列运算规律。

特别地,对于单位矩阵 E ,有
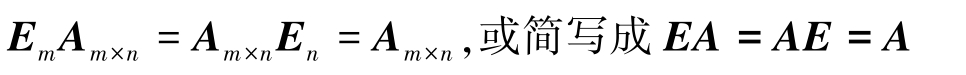
对于零矩阵 O ,有
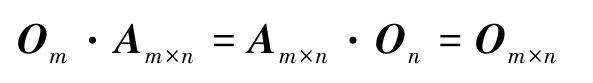
对于对角阵 Λ =diag( λ 1 , λ 2 ,…, λ n ), M =diag( μ 1 , μ 2 ,…, μ n ),有
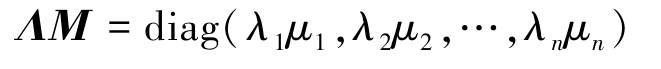
例2-9 n 元线性方程组的矩阵形式。
解 n 元线性方程组
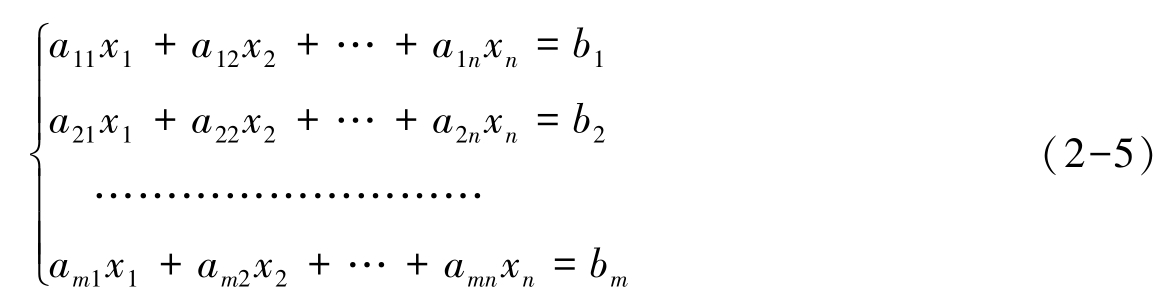
两边分别表示为矩阵,即
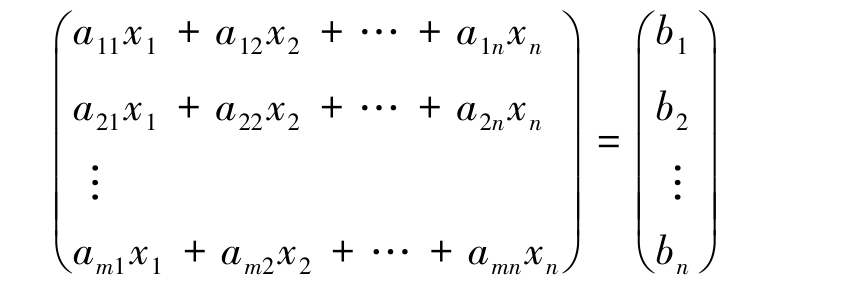
左边矩阵可以表示为矩阵乘法,即
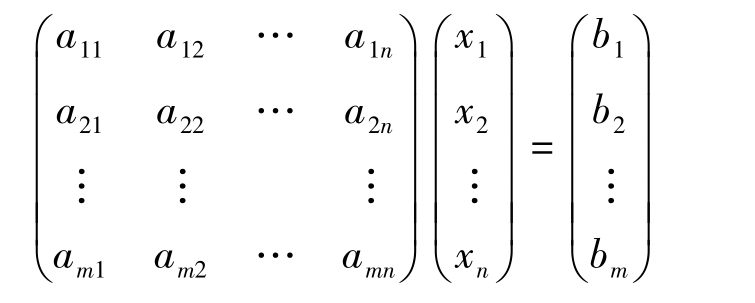
这三个矩阵分别称为系数矩阵 A m × n 、变量列矩阵 X n ×1 和常数列矩阵 b m ×1 ,则 n 元线性方程组(2-5)的矩阵方程形式可以简写为
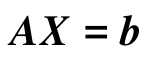
例2-10 线性变换的矩阵形式。

记
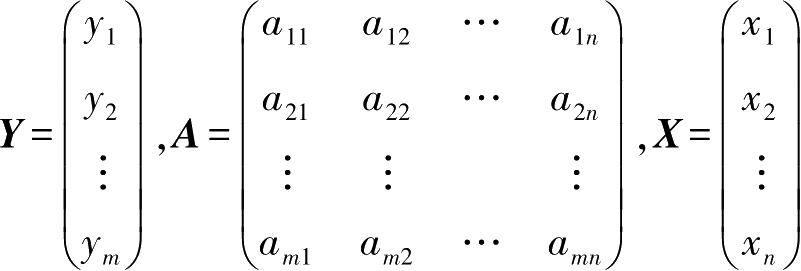 。从而线性变换(2-6)的矩阵形式可记为
。从而线性变换(2-6)的矩阵形式可记为
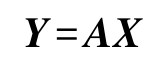
因此,引例中从 x 1 , x 2 , x 3 到 y 1 , y 2 的线性变换(2-2)矩阵形式为 Y = AX ,从 z 1 , z 2 到 x 1 , x 2 , x 3 的线性变换(2-3)矩阵形式为 X = BZ ,代入则可得到从 z 1 , z 2 到 y 1 , y 2 的线性变换为 Y = A ( BZ )=( AB ) Z 。
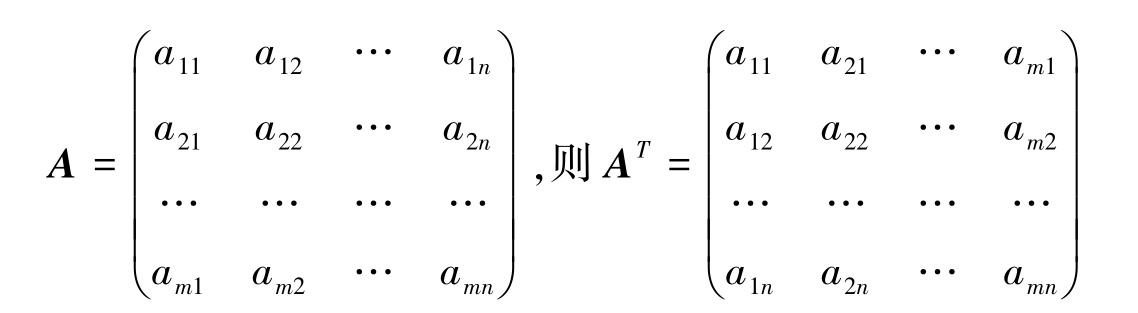
定义2-7 把 m × n 型矩阵 A 的行列互换得到的 n × m 型矩阵,称为 A 的转置矩阵,记为 A T ,即
例如,
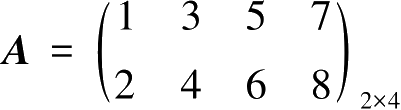 ,则
,则
 为列矩阵,则
Y
T
=(
y
1
y
2
…
y
m
)为行矩阵。
为列矩阵,则
Y
T
=(
y
1
y
2
…
y
m
)为行矩阵。
例2-11
已知
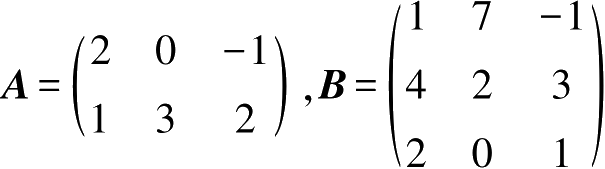 ,求(
AB
)
T
。
,求(
AB
)
T
。
解 由矩阵乘法及转置的定义,计算得到
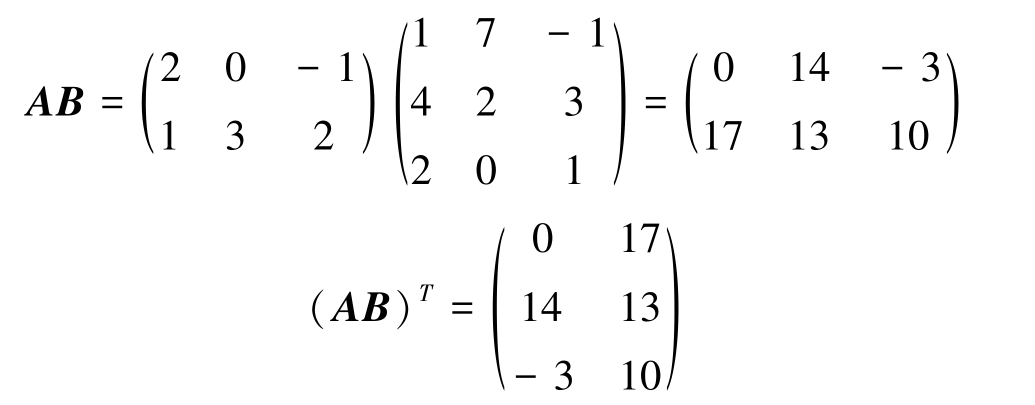
在运算可行时,矩阵的转置满足下列规律。

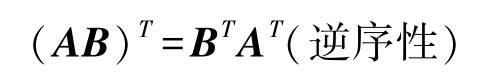
现在,证明逆序性,其余运算规律的证明留给读者完成。
证明 设 A =( a ij ) m × s , B =( b ij ) s × n , C = AB ,则 AB 的第 j 行第 i 列交叉处的元素
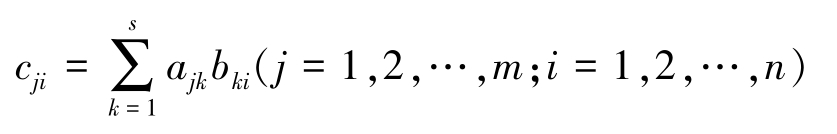
就是 C T 的第 i 行、第 j 列交叉处的元素。
而 B T 的第 i 行元素是 b 1 i , b 2 i ,…, b si , A T 的第 j 列元素是 a j 1 , a j 2 ,…, a js ,从而 B T A T 的第 i 行、第 j 列交叉处的元素是
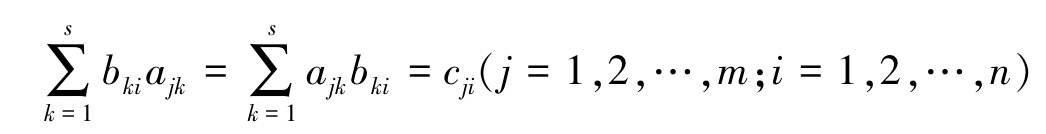
故,( AB ) T = B T A T 得证。
逆序性的结论可推广到多个矩阵的情况,即
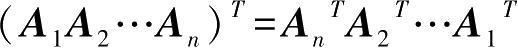 。
。
定义2-8 设 A 为 n 阶方阵, k 为正整数,方阵的幂定义为

根据矩阵乘法的结合律,方阵 A 的幂满足

因为矩阵的乘法不具有交换律,所以对于两个 n 阶方阵 A 与 B ,一般来说( AB ) k 与 A k B k 未必相等。只有当 A 与 B 可交换时,才有( AB ) k = A k B k 。类似可知,如( A ± B ) 2 = A 2 ±2 AB + B 2 、( A - B )( A + B )= A 2 - B 2 等公式也只当 A 与 B 可交换时才成立。
对于对角阵 Λ =diag( λ 1 , λ 2 ,…, λ n ), k 为正整数,有
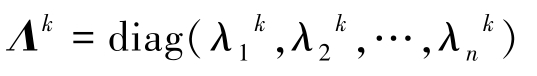
例2-12
设
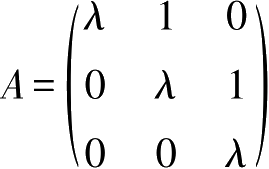 ,求
A
3
。
,求
A
3
。
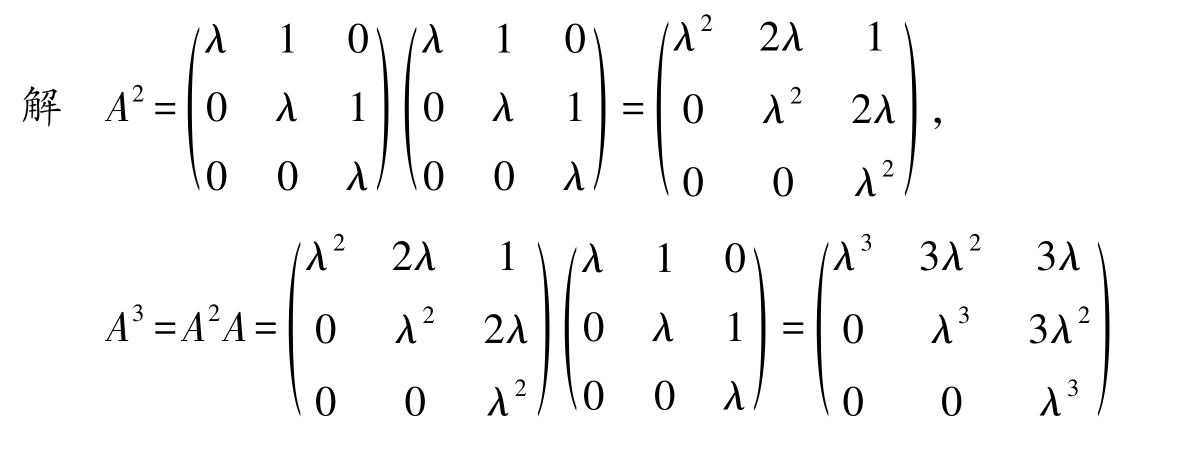
定义2-9
由
n
阶方阵
A
的所有元素保持位置不变所构成的行列式称为方阵
A
的行列式,记作
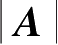 或det
A
。
或det
A
。
例如,方阵
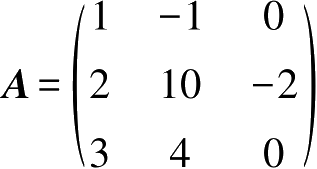 的行列式为
的行列式为
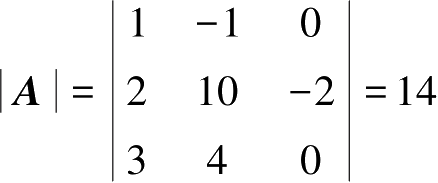 。
。
n 阶方阵 A 、 B 的行列式运算满足以下性质(其中 k 为任意实数, n 为正整数)。
(1)
(2)
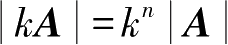
(3)
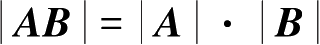
性质(3)可以推广到多个
n
阶方阵相乘的情况,
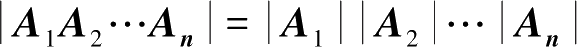 。特别地,
。特别地,
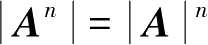 。
。
定义2-10 n 阶方阵 A 如果满足 A T = A ,则称 A 为对称矩阵,简称对称阵。对称阵的特点:关于主对角线对称的元素对应相等,即
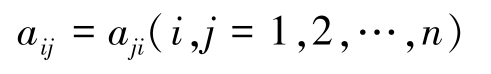
例如,
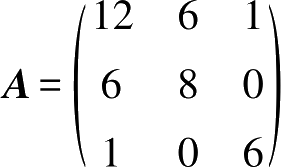 为对称矩阵。
为对称矩阵。
定义2-11 n 阶方阵 A 如果满足 A T =- A ,则称 A 为反对称矩阵,简称反对称阵。反对称阵的特点:主对角线上的元素全为0,关于主对角线对称的元素互为相反数,即
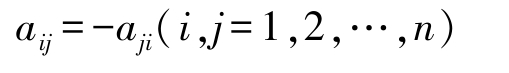
练习
1.已知3 A + X = B T ,其中
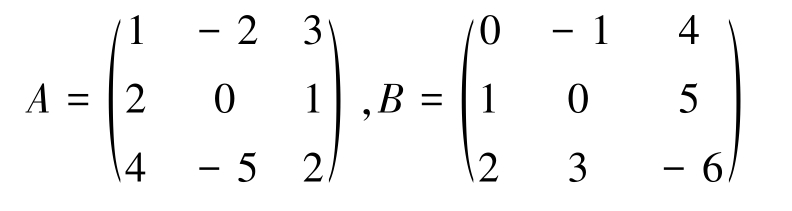
求 X 。
2.设
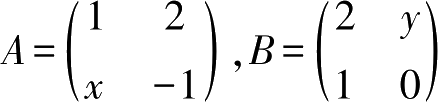 ,若
AB
=
BA
,求
x
、
y
。
,若
AB
=
BA
,求
x
、
y
。
3.完成下列运算。

4.已知两个线性变换,求从 z 1 , z 2 , z 3 到 x 1 , x 2 , x 3 的线性变换。
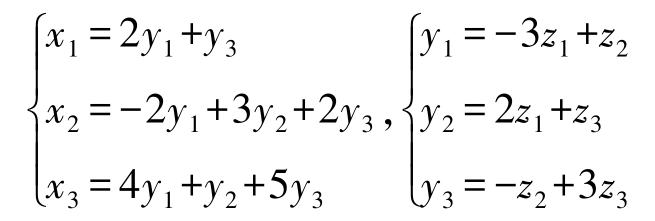
5.设
A
为三阶矩阵,且
 ,求
,求
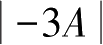 。
。
6.设 A 、 B 为 n 阶矩阵,且 A 为对称阵,证明 B T AB 也是对称阵。