




学校里的几何课教给我们一个枯燥乏味的道理:大小(或尺寸)是非常重要的。事实上,大小是物质的本质特征。角可以是锐角、直角或钝角,图形有长度、面积或体积,咸焦糖摩卡有中杯、大杯或超大杯……这些特征都可以归结为大小。对了,还有“几何”(geometry)这门学科的名字——“geo”是地球的意思,“metry”是测量的意思——就是衡量世界本身。
这种注重大小的哲学理念会冒犯到你吗?如果会,那你应该喜欢拓扑学。它的形状可以像橡胶一样伸缩,像橡皮泥一样挤压,像气球一样膨胀。事实上,它不是某种形状,而是一个变形怪。在这个像熔岩般流动的世界里,大小并不重要。事实上,“大小”甚至没有任何意义。拓扑学寻求的是更深层的真理。
没有什么比抽芽游戏能更形象地介绍这些真理。哪些点可以连接?会形成多少个区域?“里面”和“外面”的区别是什么?拿好你的帽子——或者它的拓扑等价物——享受一个任何孩子都能玩,但没有超级计算机能解决的游戏。
你需要准备什么? 2名(或更多)玩家、2支不同颜色的笔和1张纸。先在纸上画几个点。对于最初几轮游戏来说,3~4个点就足够了。
玩家的目标是什么? 抢占最后一步,让你的对手别无选择。
游戏的规则是怎样的呢?
(1)在每个回合中,玩家轮流用一条平滑的线 连接2个点(或将一个点与它自身相连) ,并在自己刚刚画的那条线上 标注一个新的点 。
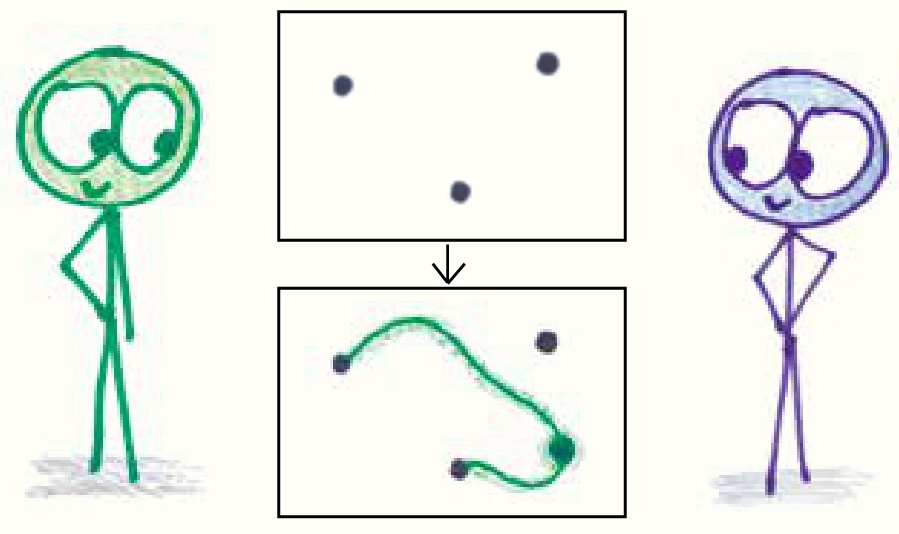
(2)只有2个限制:① 连接线 不能相交叉;② 每个点最多可以发散出3条线。
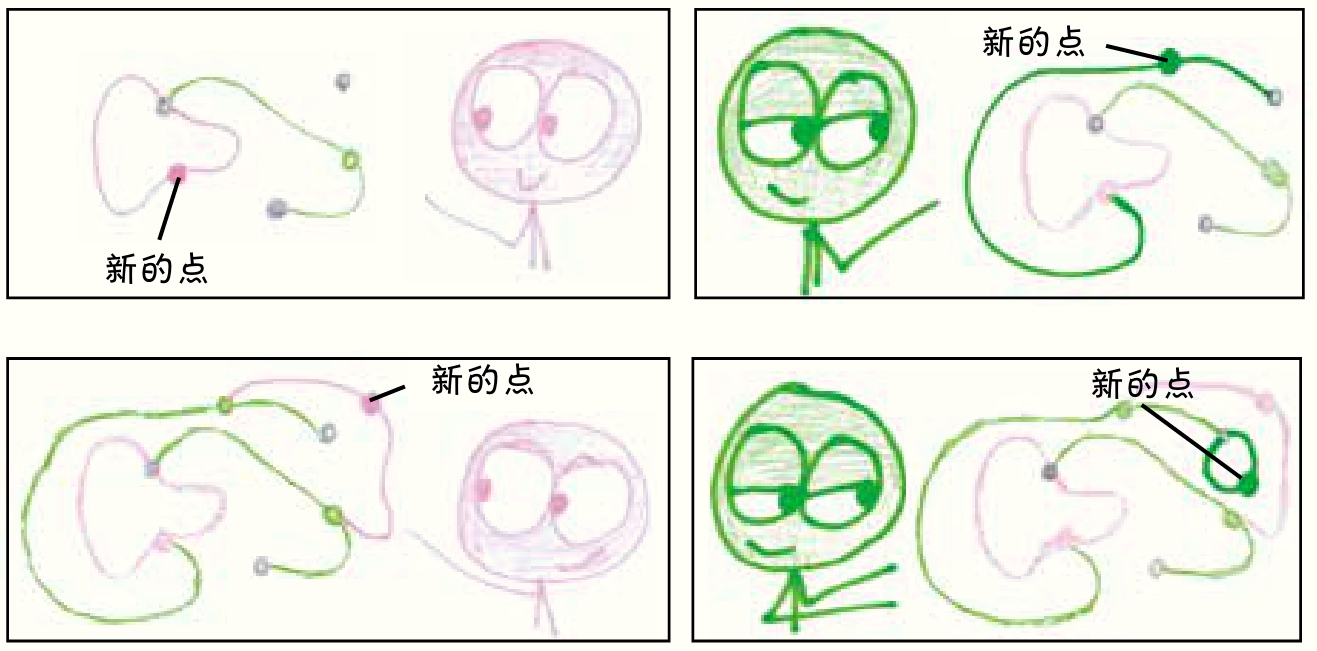
(3)最终,你们会无路可走。 谁走了最后一步,谁就是赢家 。
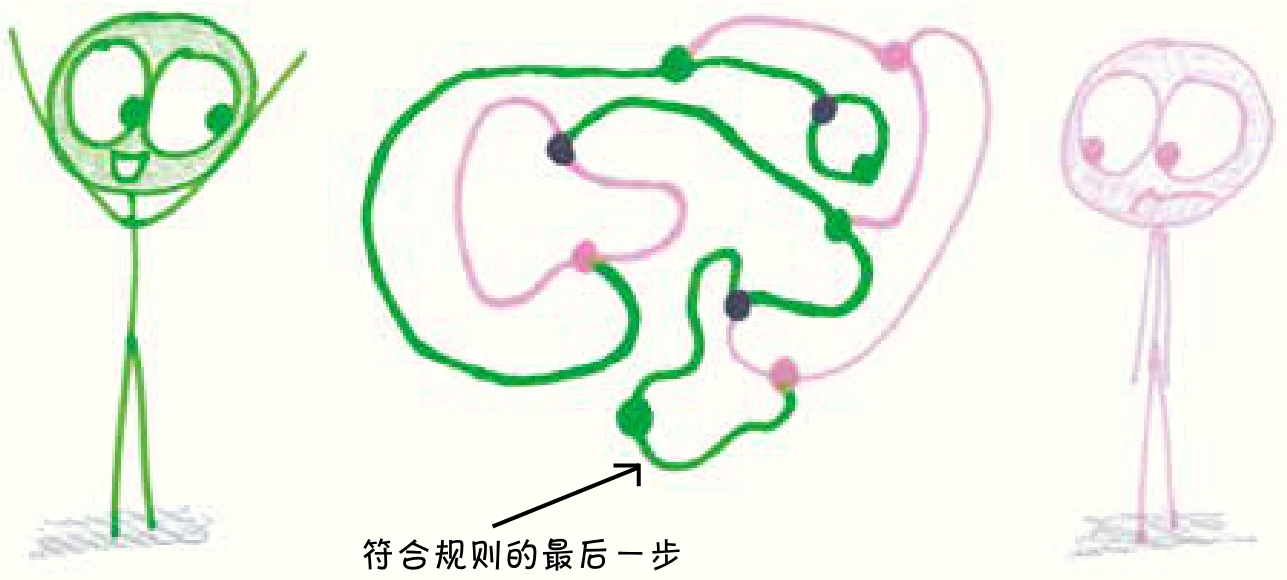
抽芽游戏的乐趣在于它的灵活性。不管你画的是短线或懒洋洋的曲线,还是迷宫般的螺旋。重要的是,你连接了哪些点。你甚至可以签上自己的名字。在我们的游戏测试中,6年级学生安吉拉发明了用抽芽游戏签名,尽管从技术上讲,这违反了“禁止交叉”规则,但它看起来实在太棒了,让人于心不忍。

这种灵活性抓住了拓扑学的精髓:看起来非常不同的东西,从功能上看,可能是相同的。
以单点游戏为例。第1个玩家必须将这个点和它自己连接起来。之后,第2个玩家必须连接图中的2个点。要实现这一点,似乎有2种不同的方式:从内部穿过,或者从外部绕过去。
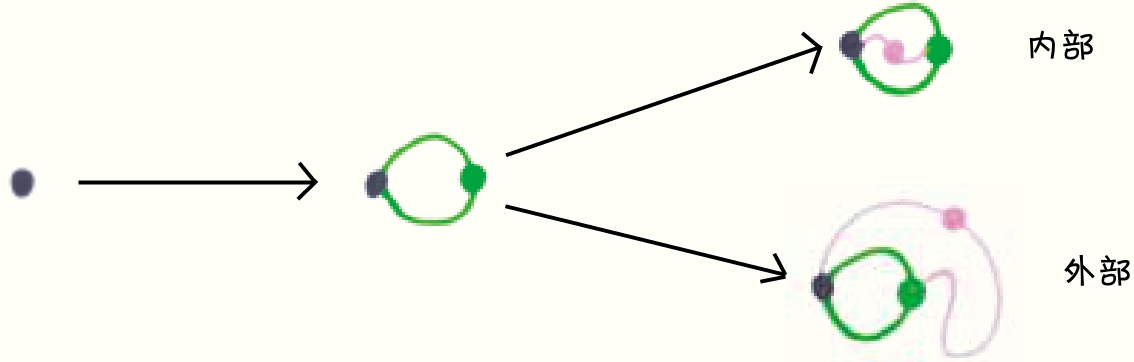
等等,想象一下如果在球体表面玩这个游戏。在这种情况下,尽管“从内部穿过”和“从外部绕过去”看起来截然不同,但实际上什么都没有改变。从拓扑学的角度来看,这2种移动是相同的。第二个玩家并没有真正的自由选择权。
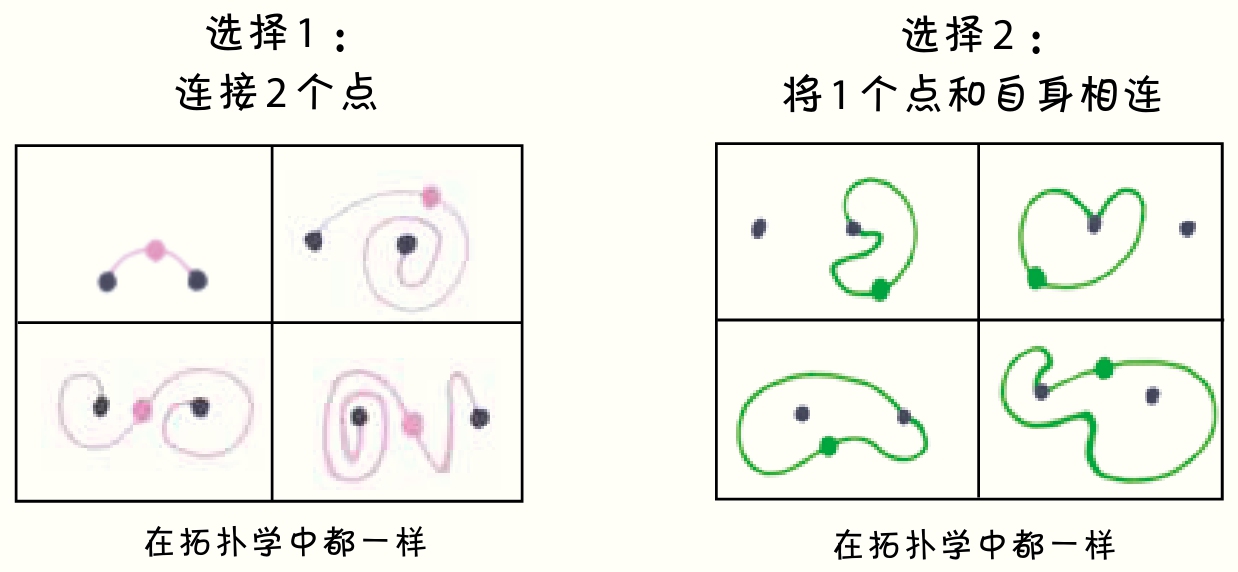
2个点的抽芽游戏是什么样的呢?从拓扑学的角度来看,玩家在开局只有两种选择:把2个点连起来,或者将其中一个点和自身相连。不管把另一个点留在“外面”还是“里面”,都无关紧要,因为在拓扑学中,这2种情况都一样。
这么说来,拓扑学家是不是会忽略所有的区别,将所有事物都视为一样的?在拓扑学中,“赢”等同于“输”吗?“好”只是“坏”的另一种表述吗?猫等同于鱼吗?如果是,我们是否应该在水族馆里放小猫砂盒?
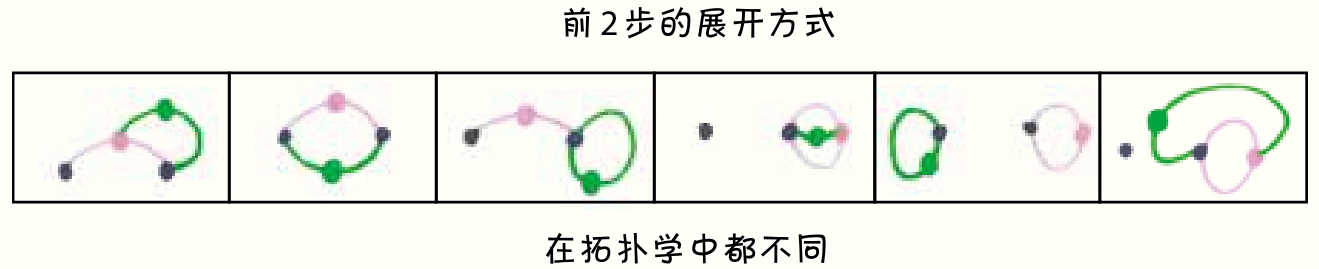
最后一个问题由你这个宠物主人做决定。但说到抽芽游戏,不必担心,并不是所有的步骤都是一样的。事实上,在2个点的抽芽游戏的第二步,你已经面临6种不同的拓扑选择。所以自此,你便获得了选择的自由。
点格棋游戏呈现给我们的是刚性的直线几何,就像一座建在网格上的城市。相比之下,抽芽游戏是一款开放的、形式自由的游戏,就像一场混乱喧嚣的嘉年华狂欢。
抽芽游戏诞生的确切时间和地点:1967年2月21日星期二下午,英国剑桥。
那天,抽芽游戏的“父母”——计算机科学家迈克·帕特森(Mike Paterson)和数学家约翰·康威,正在纸上涂鸦,试图设计一款新游戏。当时,迈克提出“添加1个新的点”的规则,约翰给游戏取了个名字,抽芽游戏就这样诞生了。
 这对欣喜若狂的“父母”一致同意将功劳按迈克60%、约翰40%的比例分配,这种友好而精确的功劳分配比游戏的诞生更令人钦佩。
这对欣喜若狂的“父母”一致同意将功劳按迈克60%、约翰40%的比例分配,这种友好而精确的功劳分配比游戏的诞生更令人钦佩。
抽芽游戏很容易玩,但几乎不可能破解。丹尼斯·莫利森(DenisMollison)曾写了一篇长达47页的分析报告,介绍如何掌控6个点的抽芽游戏。直到1990年,贝尔实验室的一台计算机才破解11个点的抽芽游戏。到我写这本书时,抽芽游戏被破解的最高点数超过40个。不过2020年,康威在去世前对这一结果的合理性提出了质疑。“如果有人说他们发明了一种机器,可以写出能与莎士比亚的戏剧相提并论的作品,你会相信吗?”他问道,“实在太复杂了。”
这样盘根错节的复杂性有没有吓跑那些只想在抽芽游戏中寻求乐趣的玩家呢?完全没有。“当抽芽游戏问世后,似乎所有人都在玩它。”康威写道,“在咖啡馆或茶舍,人们围成一个个小圈,以滑稽的姿势围观抽芽的位置……秘书人员也未能幸免……有人甚至在最不可能的地方也发现了人们在玩这个游戏……就连我3岁和4岁的女儿也在玩,”他补充道,“不过我通常能打败她们。”
因为在现代数学的所有分支中,拓扑学是①动态的;②奇异的;③实用的;④美丽的。
还有很多其他形容词可以描述它,下面让我逐一道来。
拓扑学是动态的。 拓扑学家在一个由可拉伸的织物、熔化的金属和旋转的软冰激凌组成的变形世界中遨游。无论他们走到哪里,都在寻找 不变量 的踪迹,即那些在经历了所有的剧变之后,以某种方式保持不变的特征和属性。
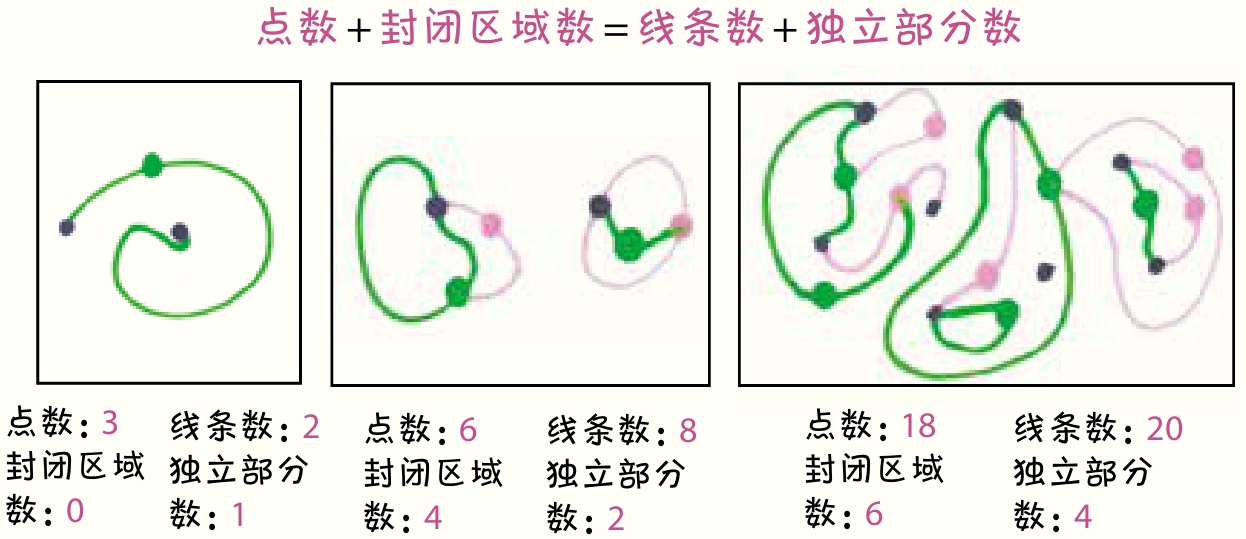
最著名的不变量是 欧拉示性数 。在抽芽游戏中,它可以归结为一个简单的等式(这个版本由埃里克·所罗门提供):点数+封闭区域数=线条数+独立部分数。
这个等式适用于所有可能出现的抽芽游戏场景,包括从游戏开始到结束,从最简单的到最复杂的环节。无论你是从2个点开始还是从200万个点开始,
点的数量加上封闭区域的数量总是等于连接点的线的数量加上独立部分的数量。

这就是典型的拓扑学:在千变万化中,我们找到了其强大的规律。
拓扑学是奇异的。 以下是约翰·康威给出的一个有趣结果。如果想让抽芽游戏的步数最少,那么游戏结束时必然呈以下形状之一:
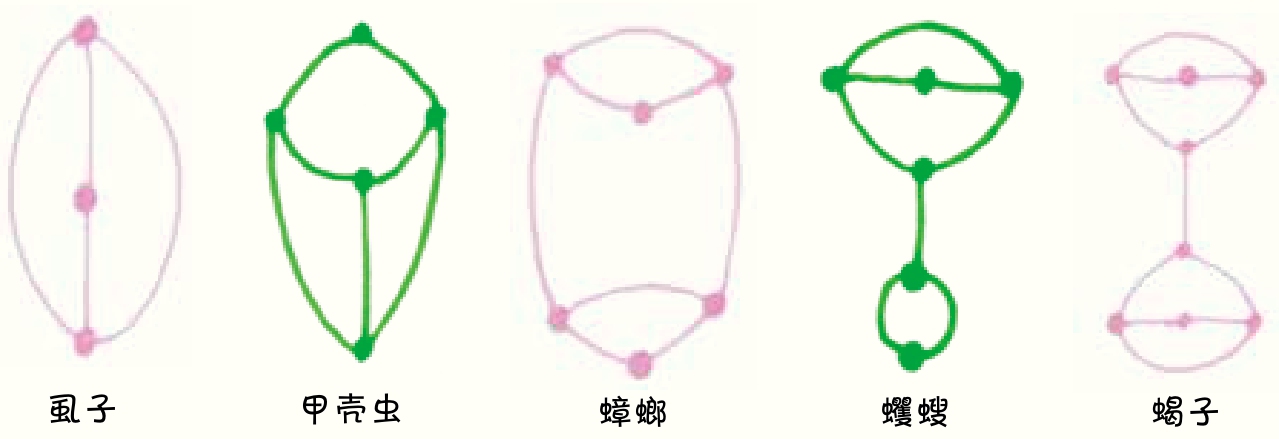
正如经典著作《数学游戏的制胜之道》( Winning Ways for Your Mathematical Plays )中所解释的:“游戏最终呈现的将是一只(可能以某种方式被翻转过来)被大量虱子(其中一些可能会感染其他昆虫)感染的昆虫构造。”
那可能会是铺天盖地的虱子。正如康威所调侃的那样有一部分构造尤其“虱山虱海”。
拓扑学是实用的。 忽略虱子和蠼螋的花哨形状,拓扑学让我们对各种事物有了更深刻的见解,从多结的DNA到错综复杂的社交网络,更不用说宇宙学和量子场论了。
以拓扑学中的一个著名问题为例: 图同构。 如你所见,在抽芽游戏中,可能会出现2种看起来不同,但包含相同结构的部分。我们要如何分辨它们是真的不同,还是表面虽然不同,但本质相同呢?
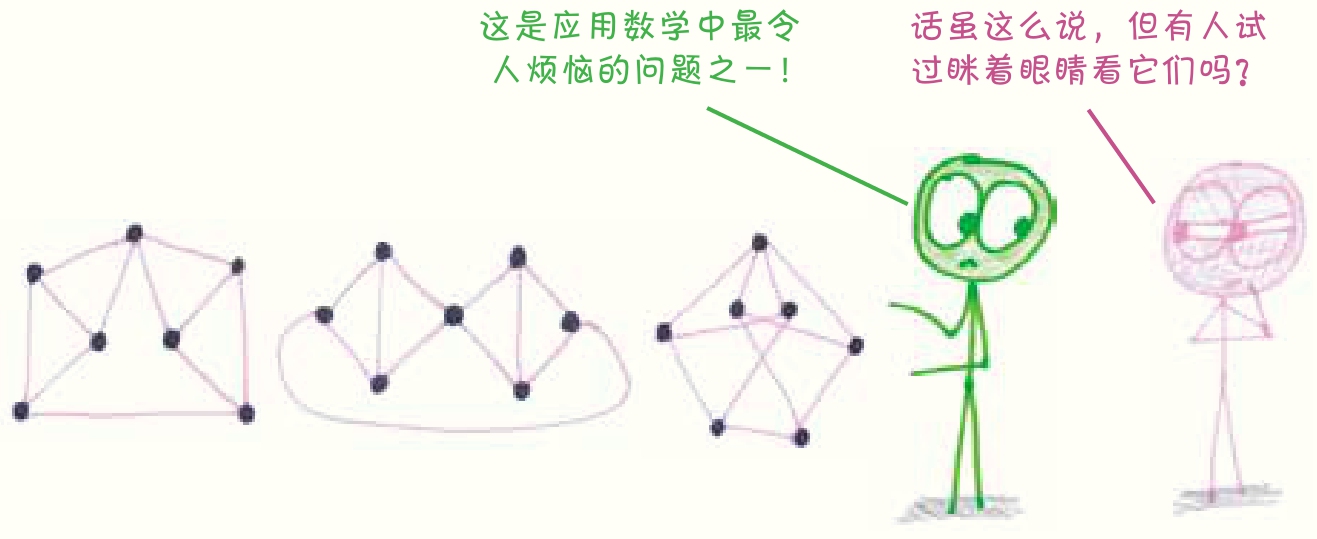
当电气工程师比较电路原理图、计算机科学家编码视觉信息、化学家在结构数据库中查找化合物时,都会遇到同样的问题。事实上,这些清醒的科学家都在玩私人定制版的抽芽游戏。
拓扑学是美丽的。 许多人第一次接触拓扑是通过莫比乌斯环,也就是把一根纸条扭转180°后,再将两头粘起来变成一个纸带圈。
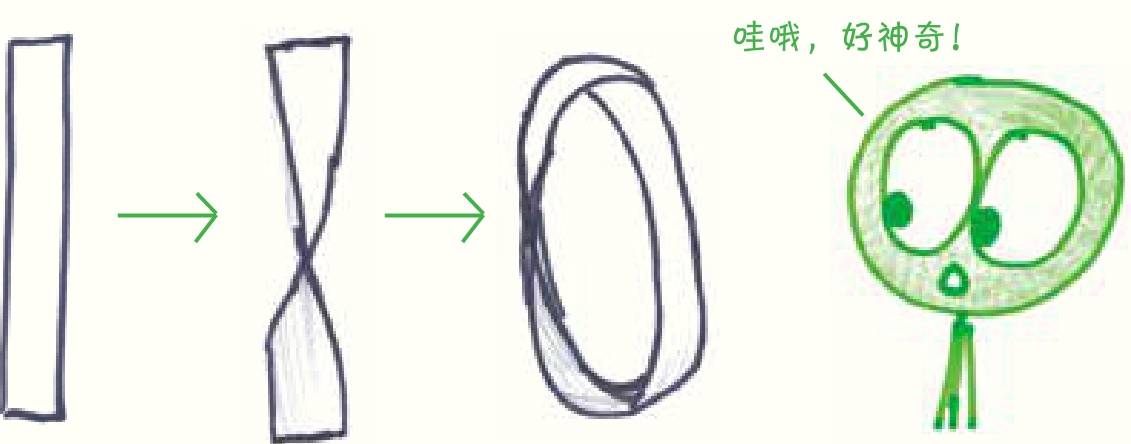
莫比乌斯环没有“内外”之分。如果你想给它像手镯一样上色,即蓝色的部分朝向手腕,红色的部分朝外,你是不会成功的。无论先涂哪种颜色,最终这种颜色都会覆盖环的整个表面。这只是它的特性之一。如果你把一条莫比乌斯环从中间剪开,会发生什么?如果把它剪成3段呢?
英国数学家大卫·理查森(David Richeson)在他的《欧拉的宝石》(
Euler's Gem
)一书中统计了拓扑学家获得菲尔兹奖(数学领域最著名的奖项之一)的次数。他写道:“在48名获奖者中,大约有
 的数学家是因为他们在拓扑学方面所做的工作而得奖,而在与拓扑学密切相关的其他领域做出贡献的人甚至更多。”
的数学家是因为他们在拓扑学方面所做的工作而得奖,而在与拓扑学密切相关的其他领域做出贡献的人甚至更多。”
如果说拓扑学的美丽来自简单性与复杂性的联姻,那么抽芽游戏一定是它们最受宠的孩子。
杂草游戏: 这个游戏由弗拉基米尔·伊格内托维奇(Vladimir Ygnetovich)设计。在每个回合中,你不是在自己刚刚画的线上添加1个点,而是要选择添加0个、1个还是2个点。
点集游戏:
在沃尔特·尤里斯设计的这个变体游戏中,除了你可以通过占领区域获得分数,其他规则与抽芽游戏一样。如果你画线后创建了一个封闭区域,就用你的初始值或颜色标记它,此区域边界上的每个点都可以得1分,此后不得在该区域内再做任何操作。当最后无路可走时,得分最多的人获胜。

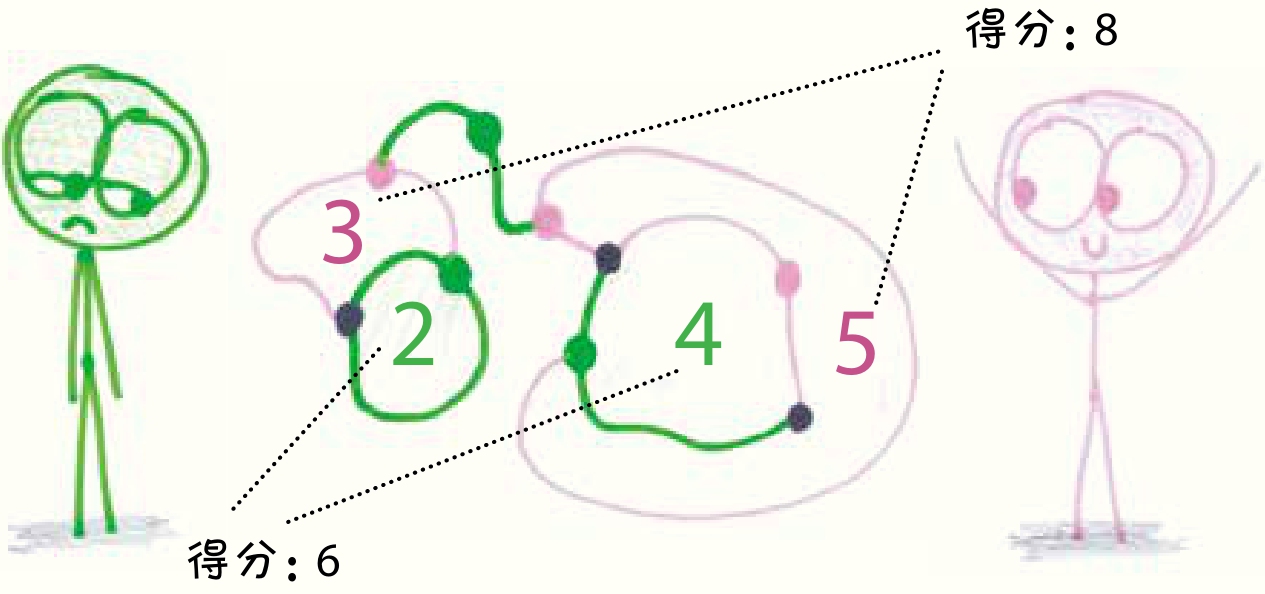
抱子甘蓝游戏: 从表面上看,抱子甘蓝游戏似乎和原版抽芽游戏一样完全是开放式且充满策略性的。但事实上,比起游戏,“抱子甘蓝”更像是狡猾的恶作剧。
这个游戏从几个“十”字开始,每个“十”字都有4个可以连接的“有空”末端。玩家轮流连接任意2个“有空”末端,然后在自己刚刚画的那条线上画一条短竖线,这样就会生成2个新的“有空”末端。注意,画的过程中不能和现有的线条交叉。画最后一条线的玩家为赢家。
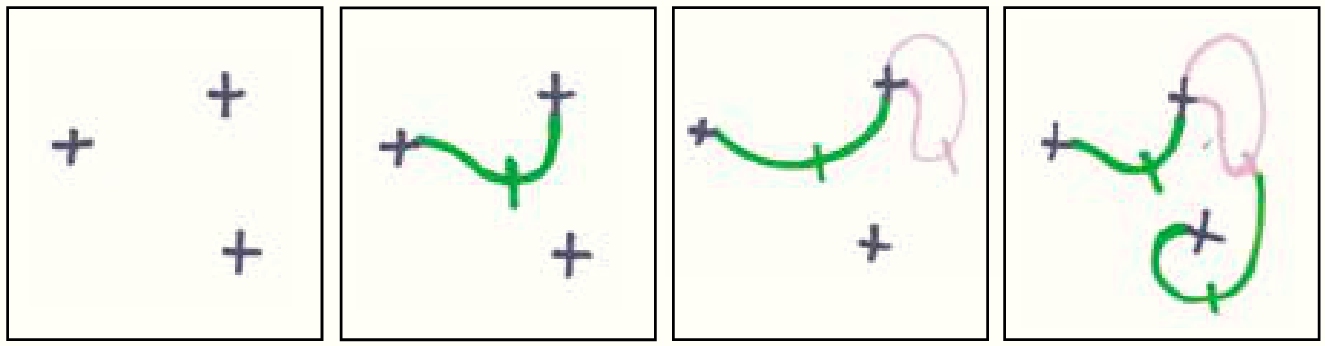
恶作剧体现在哪里呢?就是你的玩法和策略对游戏结果不会产生任何影响。起始“十”字的数量为奇数时,先走的玩家获胜;起始“十”字的数量为偶数时,后走的玩家获胜。因此,你所有的运筹帷幄和深谋远虑,与转动着玩具方向盘,想象自己在控制汽车的情形没有什么不同。
这是如何做到的呢?来,注意看,在游戏过程中,可连的末端数是不变的。每走一步就会消耗2个末端,然后再用2个新的末端替代它们。区域的数量则恰恰相反,大多数时候每走一步都会增加一个新的区域——除一些特殊的走法外。在有 n 个“十”字的游戏中,将有( n -1)步是用于连接之前未连接过的“十”字,这( n -1)步都不会增加任何新区域。
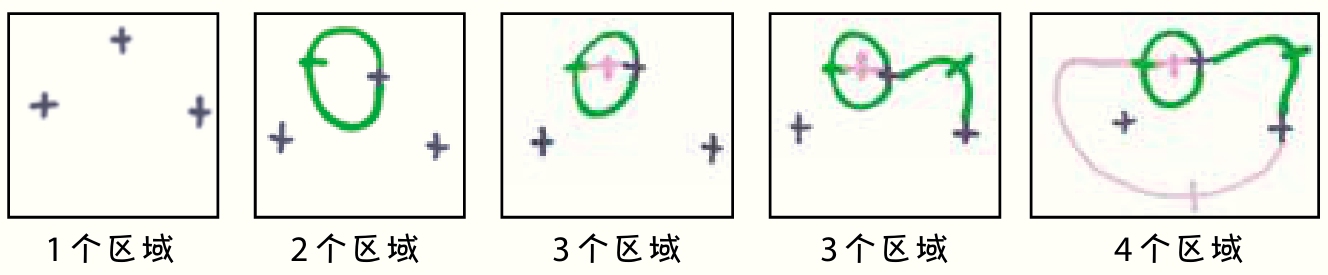
当区域的数量赶上“有空”末端的数量时,游戏结束。这需要走(4 n -1)个增加区域的步数,加上( n -1)个不增加区域的步数,总共是(5 n -2)步。
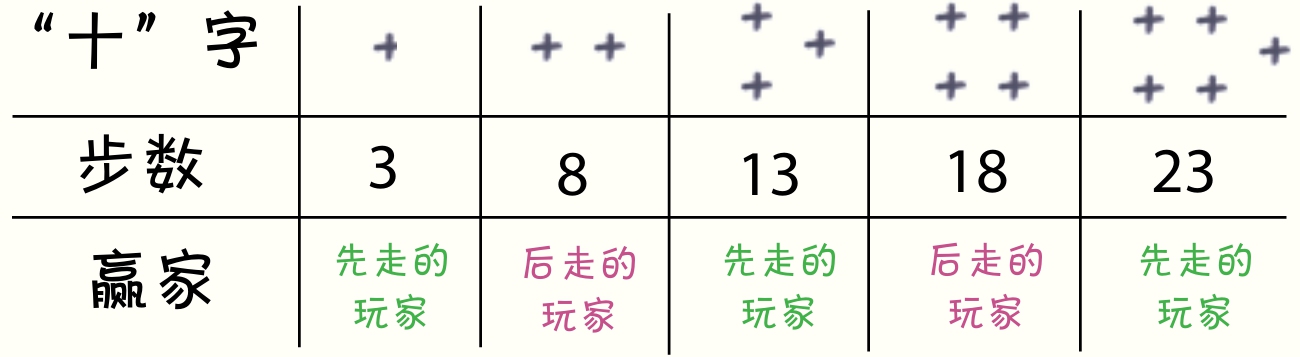
如果你想用这个恶作剧整一下好朋友,可以提议一起玩2、4或6个“十”字的抱子甘蓝游戏,每次都大大方方地坚持让对方先走。当朋友感觉到不对劲并要求你先走时,偷偷地切换成3或5个“十”字的游戏。当然,开玩笑可以,不能用这个办法骗人哦。