




我想用一个谜题拉开这本书的序幕。请问:你和黑猩猩到底有什么区别?

答案揭晓:黑猩猩在小时候是一只小猩猩,然后会长大,而你在小时候是一只小猩猩,长大后还是一只小猩猩。
我没在开玩笑,照照镜子看看你自己吧:光滑的皮肤、窄小的下颌、硕大的圆形颅骨——这些都是我们的类人猿表亲随着年龄的增长而逐渐消失的特征,而你在成长过程中却将它们固执地保留了下来。没有嘲笑你的意思啦,毕竟我也是这样过来的。人类在成年后仍保留着孩子般的特征,并执着于古生物学家史蒂芬·杰·古尔德
 所说的“永葆青春”——专业术语称为“幼态持续”(neoteny),而在灵长类动物世界中,这就是人类的特色。最神奇的是,我们不仅长得像小猩猩,行为也和它们很像,如热衷于模仿、探索、提问等。简言之,就是爱玩。
所说的“永葆青春”——专业术语称为“幼态持续”(neoteny),而在灵长类动物世界中,这就是人类的特色。最神奇的是,我们不仅长得像小猩猩,行为也和它们很像,如热衷于模仿、探索、提问等。简言之,就是爱玩。
各位长着娃娃脸的人类朋友,正是因为爱玩,我们才能成为灵长类动物中的天才选手。也正是因为爱玩,人类才能建造出金字塔、在月球上留下脚印,以及制作出全球销量超过3 000万张的专辑《艾比路》 [1] 。当然,我们并不是长大后自然而然地拥有了智慧,而是因为从小拒绝做一个愚蠢的生物。人类从动物界脱颖而出的秘密在于从未停止过学习,而我们学习能力强的秘密就在于从未停止过玩耍。
所以,还等什么呢,一起来玩吧!
你需要准备些什么呢?
(1) 一些常见的生活用品。 我尽量让大多数游戏只需用到纸和笔,但有些游戏可能还要准备些别的。每一章都详细说明了这些细节,尾声部分的表格中也有相关总结(注:骰子不一定要准备实物,在网上搜索“在线骰子”“骰子小工具”等应用就能模拟掷骰子的结果)。
(2) 玩伴。 很多数学书里的游戏都是一个人单独玩的,但本书不是。我写这本书时,正值由新冠肺炎疫情引发的保持“社交距离”(social distancing)被提出的那一年,于是它就成了一封写给社交与聚会的情书。除少数单人游戏外,你是需要玩伴的。此外,虽然本书是为像我这样的“黑猩猩大宝宝”而写的,但满10岁的孩子基本上就可以玩书中所有的游戏了,甚至还有很多游戏适合6岁左右的孩子。
新游戏本身才是最难准备的原材料。那些已有游戏的变体及相关游戏不包括在内。在法律禁止的情况下,以上建议均无效。但如果你所在的地区法律禁止玩游戏,那问题就更严重了。
(3) 回归本心。 史蒂芬·杰·古尔德写道:“许多动物在童年时期表现出高度的灵活性和玩耍的能力,但成年后却遵循着严格的既定模式。”作为一名数学老师,我不得不承认,在很多情况下,人类的数学课似乎是为其他动物(如白蚁这类刻板的模仿者)设计的。这些课程不出意料地捕捉到了我们思维中最糟糕的一面:麻木、笨拙、焦虑。阅读本书时,请抛开这一切,召唤出你真实的本性和你内心最珍贵的童心。
玩游戏的目的是什么? 最大限度地激发人类思维的潜力。
有哪些游戏规则?
(1)本书探讨的是一种独特的人类玩耍方式: 游戏, 也被称为 “规则游戏” 。它们的涵盖范围很广:从拥有无数规则(如“大富翁”)到只有一个规则(如“地上都是岩浆”),从残酷竞争的场景(如“大富翁”)到需要深度合作的场景(如“地上都是岩浆”),从最糟糕的人类文化产物(个人认为如“大富翁”)到最有价值的人类文化产物(个人认为如“地上都是岩浆”)。
在写作过程中,我一直在寻找那些规则简单且巧妙,同时能支撑丰富而复杂玩法的游戏。正如那句谚语所说:“学会一分钟,精通一世功。”
(2) “数学游戏”具体指的是什么? 这是个好问题。第一个问我这个问题的是维托·索罗(Vito Sauro),他是明尼苏达州最友善的桌游专家之一。他指出,几乎所有桌游都是由数学框架和某种主题的外壳构成的,所以我这本书会涵盖所有已经问世的游戏吗?
① 英尺约等于0.3米。——译者注
我告诉维托:并不会。在我的定义中,数学游戏是一种让你觉得“哦哦哦,这的确很数学”的游戏。
面对我的回答,维托认为说了等于没说,但他对此已经很满意了。不管怎样,我一直在尝试设计与
逻辑、策略和空间推理
有关的经典游戏,而设计的三个标准如下:①有趣;②容易玩;③在数学上给人启迪。

(3)这本书介绍了5大类游戏: 空间游戏、数字游戏、组合游戏、风险与回报游戏,以及信息游戏。 以上分类只是我的灵光一现,并不严谨,切勿将其看作每个样本都能被归档的完美分类学。它们更像是一种氛围灯,用于突出游戏鲜明的特征。例如,国际象棋可以被归为这五大类中的任意一类,它在不同的光源下看起来略有不同。
以上每个大类的游戏各占一章,每章都以一篇介绍数学相关分支的有趣文章拉开序幕,紧接着推荐 5款有特色的游戏 ,每款游戏占一节,大致按照复杂性不断增加的顺序排列(但每章都是全新的开始),最后是对多个游戏的简要介绍(其中有几个我非常喜欢)。
(4)每款精选游戏都遵循相同的程序做介绍。首先,在 “这个游戏怎么玩?” 中,我将列出游戏的机制,包括你需要准备什么、玩家要实现的目标,以及游戏规则。
然后,在
“游戏体验笔记”
中,我将详细阐述游戏玩法的特色,尝试将那些只可意会不可言传的滋味描述清楚。你可能会得到一些游戏策略上的建议,但那不是我的目的。我只是想厘清数学游戏中微妙的色调和阴影,其中的变化如此精妙,可能会让葡萄酒看起来像糟糕的陈年葡萄汁。

① 余味,围棋术语,一般指不要过早定型,保留变化,根据棋局的进程再来决定怎么下。——译者注
② 手筋,围棋术语,指棋手处理关键部分时所使用的手段和技巧。——译者注
接下来,在 “这个游戏从何而来?” 中,我会告诉你我所知道的这些游戏的起源。有些是流传了多年的古老游戏,有些是新鲜出炉的青涩游戏,还有些二者兼有(不要问我这是怎么回事,情况就是这么个情况)。
再下来,在 “为什么这个游戏很重要?” 中,我将告诉你这款游戏为何能激发人类最好的思维。或许是因为它模拟了物质的量子结构;或许是因为它揭示了拓扑学的朴素之美,或者美国选区划分中不公正的冷酷逻辑;又或许是因为它能释放你内在的天赋,唤醒你体内那只沉睡已久的“黑猩猩”。不管怎样,我认为这是这一节的关键,也是我写这本书最重要的目的。
最后,在 “变体及相关游戏” 中,我将提出一些有趣的方向,你可以在其中尽情探索。在这些变化中,有些是对规则的微调,而有些则是在历史、概念或精神等方面与原版游戏有所关联的全新游戏。
(5)在本书的结尾,我列出了一个详尽的表格,包含书中所有的游戏,以及大家喜爱的以问答形式呈现的参考文献。
哦,对了,我还会解释自己是如何在本书中创造出
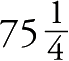 种游戏的。如果你现在就想问:“那
种游戏的。如果你现在就想问:“那
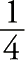 种游戏是怎么回事?”请你大可放心,我在结尾部分解释的内容比这复杂得多。
种游戏是怎么回事?”请你大可放心,我在结尾部分解释的内容比这复杂得多。
如果你愿意,你可以把它当作一部普通的非虚构作品。一页页翻过去,在看到笑话时礼貌的微笑,然后喃喃自语:“我的天,这画画技术也太糟糕了,买书的钱花得可‘真值’。”一章接着一章、一个游戏接着一个游戏,你会度过一段非常愉快的时光,但你也会错过所有真正的乐趣。
这本书是用来玩的。人类就应该玩各种各样的数学游戏,就像大象玩它的长鼻子、鸟儿玩它的翅膀,或者“蝙蝠侠”玩他的豪车,这应该是人类与生俱来的兴趣。人类的数学思维能力是一种非凡的天赋,除无法破解猫的高冷傲娇之外,堪称动物界无可匹敌的力量。所以,千万别把这个好不容易才进化来的“礼物”留在包装纸里,把它拿出来,玩起来。或者至少像猫一样,玩一玩包装纸吧。
本书中的大多数游戏都是多人游戏。我希望你能找到一个愿意分享好奇心的玩伴,和他一起在游戏中探索,边玩边分析。数学家玛丽·埃佛勒斯·布尔(Mary Everest Boole)说:“在竞争大行其道的地方,只有死掉的数学才能被教授。鲜活的数学必须永远是公共财产。”但在我看来,即使是竞争性的游戏也是协作项目,而在竞争性游戏中,玩家将他们的头脑联合在一起,形成了非凡的逻辑和策略之链。国际象棋大师大卫·布龙斯坦(David Bronstein)将其称为“两个人的思考”,著名精神病学家卡尔·门宁格(Karl Menninger)称之为“思想的渐进式渗透”,而我则称之为“玩耍”。
总之,我希望你能读读这本书。从组合爆炸到信息论,其中的每个游戏都揭示了数学的深层真理。反过来,这些数学真理的光芒又照亮了我们的游戏。别担心它们会亮得刺眼,你的眼睛会适应的。正如英国牧师查尔斯·凯莱布·科尔顿(Charles Caleb Colton)所说:“数学的研究就像尼罗河一样,始于微小,终于宏大。”
书中的游戏来自法国巴黎的大学、日本的校园、阿根廷的杂志、厚脸皮的吹牛大王、喧闹的赌场、喝得醉醺醺的学者、谦逊的数学业余爱好者,以及精神亢奋的孩子。这些游戏之所以变化多端,是因为数学变化多端;之所以冒着傻气,也是因为数学冒着傻气。数学游戏属于所有人,因为无论那些令人生畏的公式和喜欢冷嘲热讽的学院派人士怎么说,数学都属于所有人。
总的来说,本书中的游戏主要来自以下4个领域:
(1) 传统的儿童游戏 ,如战舰游戏、筷子游戏和点格棋。
(2) 休闲娱乐的桌游 ,如Teeko游戏、纸上拳击和亚马逊棋。
(3) 由数学家设计的概念游戏 ,如SIM游戏、抽芽游戏和多米诺工程。
(4) 古怪但有趣的课堂游戏 ,如邻居游戏、离谱游戏和“到101就输了”。
这些游戏是怎么产生的呢?是什么点燃了数学之火?我自己设计了9款游戏,按理来说,我应该知道问题的答案。然而,答案却是,没有唯一的路径。这些游戏并不存在共同的起源。印度带给我们国际象棋
 ,中国带给我们围棋,马达加斯加带给我们迂棋
,中国带给我们围棋,马达加斯加带给我们迂棋
 ,而我2岁的侄子斯坎德尔为我们带来的则是“围着问题跳舞,口中还喊着‘哇呜哇呜’”。
,而我2岁的侄子斯坎德尔为我们带来的则是“围着问题跳舞,口中还喊着‘哇呜哇呜’”。
为什么数学游戏如此普遍?说实话,我不知道答案,也许是因为宇宙本身就充满了数学。
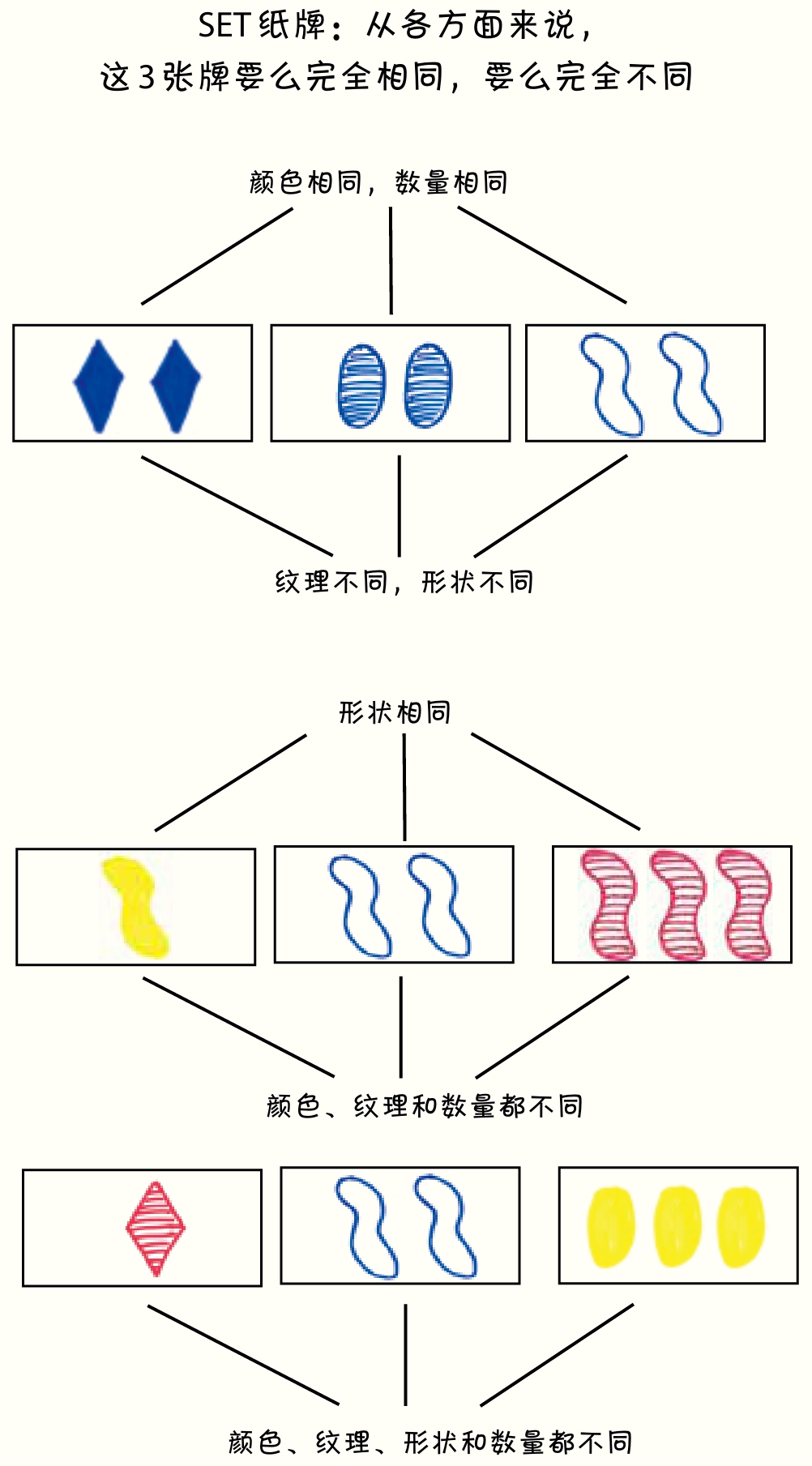
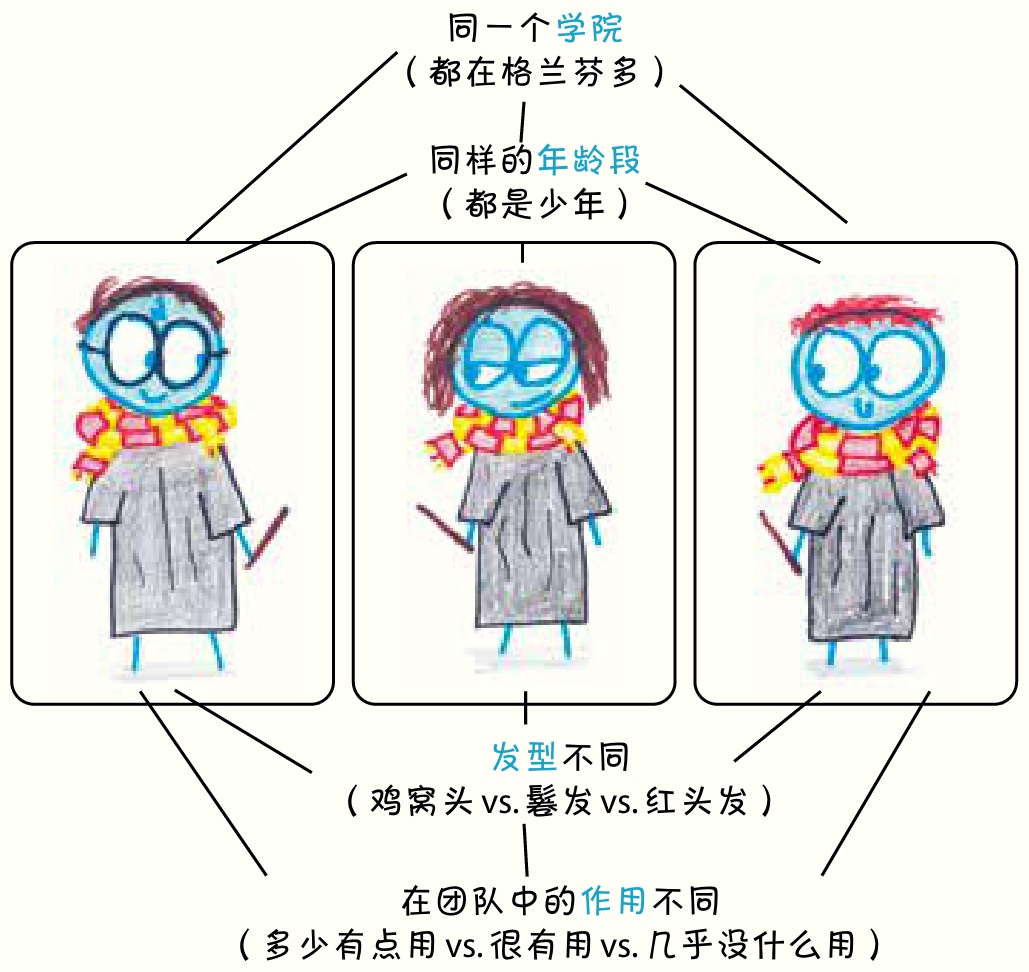
举个例子:1974年,遗传学家玛莎·让·法尔科(Marsha Jean Falco)开始在索引卡上画符号。这是一个研究工具:每张卡代表一只狗,每个符号代表狗基因组中的一个DNA序列。但随着她不断地洗牌和重新排列,所有的细节都消失了,她开始看到纯粹的组合和抽象的图案。这就是逻辑游戏。法国数学家亨利·庞加莱(Henri Poincaré)写道:“物质不会吸引(数学家的)注意力,他们只对形式感兴趣。”玛莎开始跳脱出兽医的视角看问题,并在不久后想出了一个游戏。
就这样,史蒂芬·霍金(Stephen Hawking)最喜欢的消遣方式、顶尖数学家最喜欢的研究课题,以及20世纪最受欢迎的纸牌游戏之一——SET纸牌——诞生了。
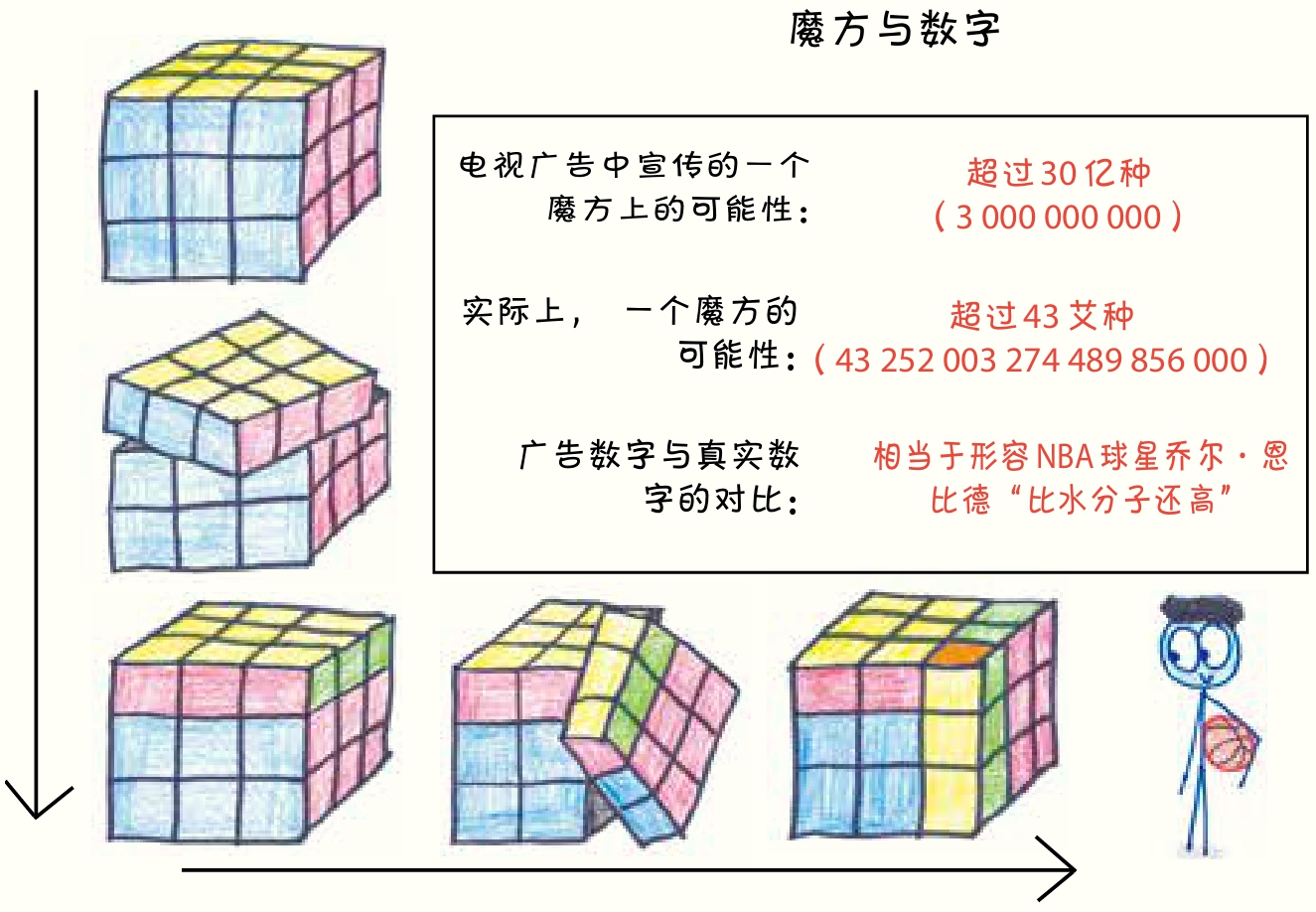
同年,匈牙利建筑师厄尔诺·鲁比克(Ernő Rubik)给自己设定了一个结构上的挑战:是否可以把许多独立的小方块积木拼成一个大方块积木?经过一番尝试后,他成功了。接下来,他又突发奇想,在大方块积木的每一面都贴上彩纸,然后开始扭动它。他后来回忆道:“这场彩色之旅让我感到心满意足。但最终,就像在一段愉快的旅程即将结束之际,已经看了许多旖旎的风景,我认为是时候回家了——该把小方块们放回原位了。”
经过一番尝试,他失败了。爱玩的他屡战屡败,但从未停止尝试。经过1个月的努力,他终于将这个立方体恢复到了原来的状态。
就这样,魔方诞生了,并成为人类历史上最畅销的玩具之一。
SET纸牌和魔方向我们展示了数学思维的两条基本路径:你可以像玛莎那样从现实的一角开始,寻找它的抽象结构;或者你也可以像厄尔诺那样从一个抽象结构开始,在现实中寻找它的意义。从这个意义上说,SET纸牌和魔方不只是用来玩的游戏,它们本身就是游戏思维的成果,是那些从不停止学习的天才猩猩所创造的闲散艺术。
因为它们能激发人类思维中最好的部分。
1654年,有个赌徒在写给数学家布莱兹·帕斯卡
 和皮埃尔·德·费马
和皮埃尔·德·费马
 的信中提出了一个谜题。这个谜题是这样的:两个人在玩简单的概率对半游戏,每赢一局可得1分。最先得到7分的人可获得100法郎奖金。但在比赛进行到一半时,比赛中断了,此时其中一方以6:4领先。在这种情况下,怎样分配奖金才公平?
的信中提出了一个谜题。这个谜题是这样的:两个人在玩简单的概率对半游戏,每赢一局可得1分。最先得到7分的人可获得100法郎奖金。但在比赛进行到一半时,比赛中断了,此时其中一方以6:4领先。在这种情况下,怎样分配奖金才公平?
这两位数学家解决了这个问题, [2] 更棒的是,他们的解法促成了对不确定性的数学研究,即今天人们所熟知的概率论。
没想到吧?概率论作为一个现代的基本工具,竟然诞生于一个关于机会游戏的简单谜题。
另外,还有一个真实的故事。18世纪,每到周日下午,柯尼斯堡(今天的加里宁格勒)的居民都喜欢在这座河滨城市的4个区之间闲逛,旨在找到一条既能一座不落地穿过城内所有的桥(共7座)——铁匠桥、连接桥、绿桥、商人桥、木桥、高桥和蜜桥,又能保证每座桥只经过一次的路线。但是没有人能做到。1735年,瑞士数学家莱昂哈德·欧拉(Leonhard Euler)证明了他们失败的原因。从数学层面来看,这是不可能做到的,这样的路径也不可能存在。今天,我们将他的证明视为“图论”(graph theory)的开端,图论是对网络的研究,它奠定了社交媒体、互联网搜索算法及流行病学等事物的根基。谷歌、脸书(Facebook)和如今人类抗击新型冠状病毒肺炎(COVID-19)的斗争都可以追溯到普鲁士人的这项午后娱乐活动。
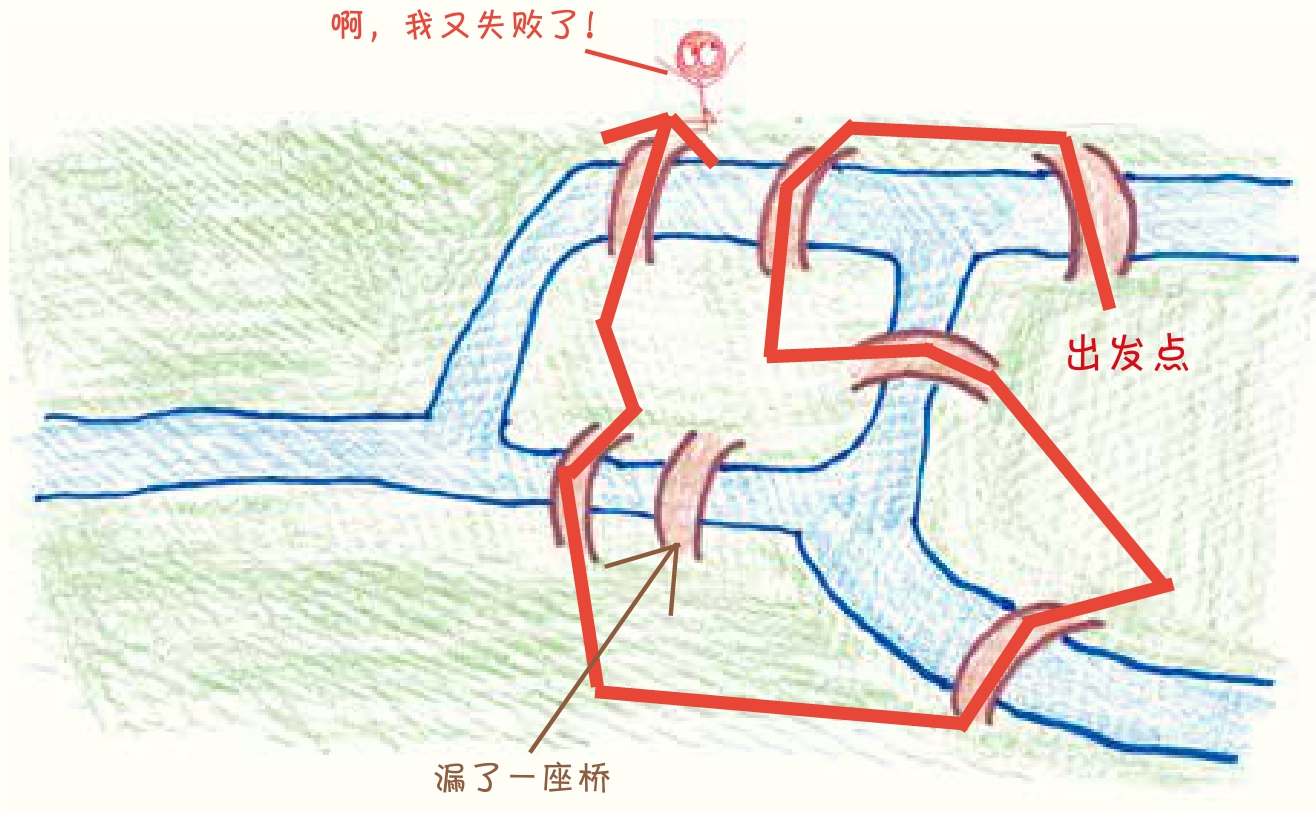
还要我再举一个例子吗?那就说说约翰·康威(John Conway)吧。他是一位传奇的数学家,在我写这本书期间去世了。从细胞自动机到抽象代数,康威探索了各种各样的数学。然而,他一次又一次地回到游戏中。他本人最得意的发现是超实数,它将双人游戏的结构编码成一个数字系统。而他最受瞩目的(也是他最不以为然的)发现——生命游戏,则展现了这个世界的复杂性是如何从一些简单的规则中产生的。
“我被他关于游戏的想法深深打动了,”康威的崇拜者、数学家吉姆·普罗普(Jim Propp)写道,“游戏的想法在他关于晶格、代码和包装的研究中发挥了作用……一个热爱游戏的数学家发现,游戏恰好是他所研究的其他学科的基础,这是何等的幸运。”

我还有很多诸如此类的例子——每周一次的“扑克之夜”启发约翰·冯·诺伊曼
 提出了博弈论,如今,他的战略性洞见已经渗透到生态学、外交和经济学领域——但我不是要歌颂这些应用。我并不关心数学游戏是否造就了亿万富翁或创造了数万亿美元的财富。我想说的是,这些结果是数学游戏中带有偶然性的副产品。
提出了博弈论,如今,他的战略性洞见已经渗透到生态学、外交和经济学领域——但我不是要歌颂这些应用。我并不关心数学游戏是否造就了亿万富翁或创造了数万亿美元的财富。我想说的是,这些结果是数学游戏中带有偶然性的副产品。
当你从游戏中抬起头,意识到自己在不经意间改变了人类历史的进程时,你会发现自己在玩一种特殊的“火”。
马森·哈特曼(Mason Hartman)写道:“一切好的思考都是游戏。”她的意思是,探索想法最好的方式应当像小猩猩探索森林一样,带着一种自由和舍弃的精神。这不是玩飞行棋,走的每一步都是为了胜利。相反,这是一个关于假装和想象的游戏,一个告诉自己“是的,然后……”的游戏,一个代代相传的游戏,一支永不熄灭的火炬。“玩一个有限游戏的目的是获胜,”詹姆斯·卡斯(James Carse)写道,“而玩一个无限游戏的目的是让游戏不要停下来。”
数学在我们眼中通常是一个个有限游戏:待回答的问题,待解开的谜题,待证明的定理。然而,当它们汇聚起来时,便构成了一个永无止境的宏大游戏,几乎囊括了每个已开化猿类的思想。“我爱数学,”数学家罗莎·彼得(Rózsa Péter)说,“既因为人类把自己玩耍的精神注入其中,也因为它给人类提供了最伟大的游戏——无限游戏。”
尽管我个人认为人类最伟大的游戏应该是“地板是熔岩”,但我偶尔也会从无限游戏中获得乐趣,诚挚地邀请你也加入进来。
[1] 《艾比路》( Abbey Road ),英国摇滚乐队披头士于1969年发布的第11张专辑,也是他们的最后一张录音室专辑。——译者注
[2]
剧透一下,落后的玩家获胜的唯一希望是赢得接下来3轮的每一轮。而这一情况发生的概率是
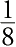 。因此,该玩家应获得奖金的
。因此,该玩家应获得奖金的
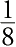 ,即12.50法郎,而领先的玩家应得到87.50法郎。
,即12.50法郎,而领先的玩家应得到87.50法郎。
