




1.试证明网络的级联能力不会超过1/2。
2.方形点格键逾渗和座逾渗的逾渗阈值 p c 分别为多少?
3.请问ER网络和无标度网络的理论逾渗阈值分别为多少?
4.利用程序模拟占据概率为0.59的二维晶格座逾渗模型,晶格大小分别为10、20、50、100。
5.利用Python语言编程实现独立级联模型。
6.设想一种信息级联模型,假设每个个体顺序决定是否采用一项新技术,而且每个接受新技术的人会得到正或负的回报。这些回报是随机的,平均来看,如果技术足够优秀回报就是正数,否则回报是负数;任何决定拒绝该技术的人得到的回报为0。此外,每个个体在进行决策时可以观察到前面所有人得到的回报:
1)假设这项新技术其实效果并不好,那么这些回报信息对采用这项新技术的信息级联会产生怎样的影响?
2)假设这项新技术效果非常好,那么拒绝该项技术的级联是否有可能发生?
7.假设你是一家公司的HR,现在部门领导要求你解释一个近期的招聘错误决定。公司面试两个候选人 A 和 B ,他们竞争同一个岗位。所有的HR全部参加面试并一起决定聘用哪一个人,每一个HR都希望选择一个最合适人选,然而面试之后,每个HR对两个人谁是最佳选择有不同看法。做最终决定时,每个HR宣布自己认为的两个候选人中的最佳人选。结果是,每个人都认为候选人 A 最合适,因为没有再进行讨论,便决定录用 A 。现在 A 工作了一段时间之后,大家又开始觉得实际上录用 B 是最好的选择:
1)老板确信在开会之前,至少有一些HR认为候选人 B 是最佳人选,那么为什么开会时大家一致支持候选人 A 。你如何向老板解释这一原因?
2)你能否设计另一种机制,使得委员会成员可以透露对候选人的初步不同意见,并且也能够让候选人 B 得到这份工作的机会更大一些。
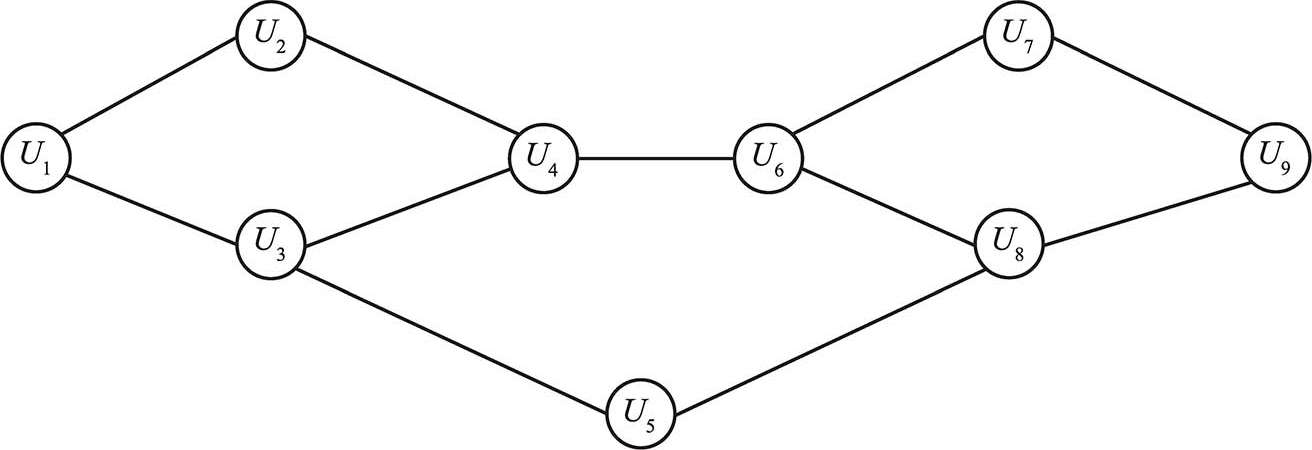
图1-21 第8题图
8.考虑如图1-21所示的网络,假设每个节点开始采用行为 B ,每个节点转而采取行为 A 的门槛值为 q =1/2:
1)设节点 U 1 和 U 4 组成一个行为 A 的初用节点集 S ,如果其他节点遵循门槛规则选择行为,那么哪些节点最终会转向行为 A ?
2)在图1-21中的 S 之外找出一个密度大于1- q =1/2的聚簇,当行为 A 以 S 为开始集合, q 为门槛值时,这个聚簇阻碍 A 传播到所有其他节点。
9.考虑如图1-22所示的社会网络,假设每个节点开始采用行为 B ,每个节点转而采取行为 A 的门槛值为 q =2/5:
1)设节点 U 1 和 U 2 组成一个行为 A 的初用节点集 S ,如果其他节点遵循门槛规则选择行为,那么哪些节点最终会转向行为 A ?简要解释即可。
2)求不包含 S 密度大于1- q =3/5的聚簇,它能阻止行为 A 传播到所有节点,设该过程从 S 开始且门槛值为 q 。
3)假设允许在指定的网络中添加一个边,从节点 U 1 或 U 2 连接到任何一个当前未连接的节点。是否存在这样一种连接方式,使得以初用节点集 S 开始,门槛值为2/5,最终行为 A 将传播到所有节点?
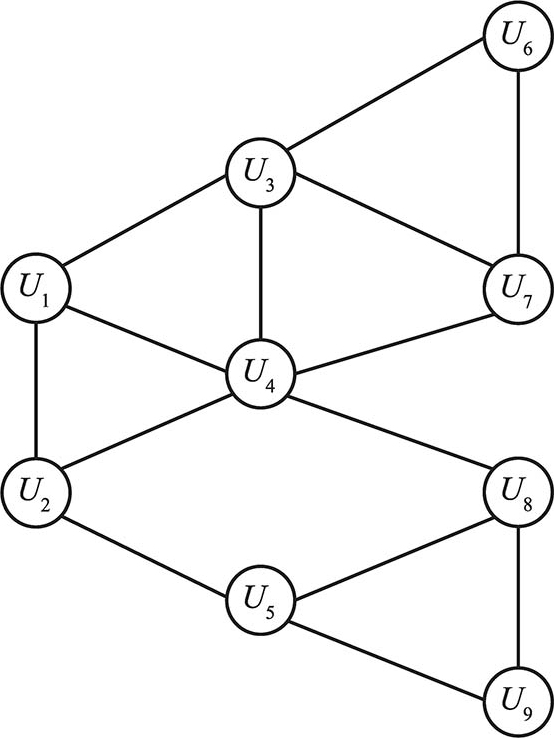
图1-22 第9题图
10.考虑1.2.1节中介绍的协调博弈模型,如果节点 v 和 w 都试图决定是选择行为 A 还是 B ,则:如果 v 和 w 都选择行为 A ,它们分别得到收益 a >0;如果它们都采用 B ,则分别获得收益 b >0;如果它们采取相反的行为,分别获得收益0;并且任何一个节点的总收益取决于该节点与每个邻居进行这种协调博弈得到的收益和。现在考虑一个更一般化的模型,当节点与邻居节点采取不同的行为时,得到的收益不为0,而是一些小的正数 x ,即 如果与邻居节点采取相反的行为,它们分别得到收益 x ,其中 x 是一个小于 a 和 b 的正数 。那么在该模型变体中,每个节点的决策是否依然基于门槛规则?具体来说,是否可以形成一个以变量 a 、 b 、 x 形式表达的临界值 q 的公式,且如果每个节点 v 至少有比例为 q 的邻居采用 A ,也会采用行为 A ,否则将采用 B ?