




1.试证明网络的级联能力不会超过1/2。
2.方形点格键逾渗和座逾渗的逾渗阈值 p c 分别为多少?
3.请问ER网络和无标度网络的理论逾渗阈值分别为多少?
4.利用程序模拟占据概率为0.59的二维晶格座逾渗模型,晶格大小分别为10、20、50、100。
5.利用Python语言编程实现独立级联模型。
6.设想一种信息级联模型,假设每个个体顺序决定是否采用一项新技术,而且每个接受新技术的人会得到正或负的回报。这些回报是随机的,平均来看,如果技术足够优秀回报就是正数,否则回报是负数;任何决定拒绝该技术的人得到的回报为0。此外,每个个体在进行决策时可以观察到前面所有人得到的回报:
1)假设这项新技术其实效果并不好,那么这些回报信息对采用这项新技术的信息级联会产生怎样的影响?
2)假设这项新技术效果非常好,那么拒绝该项技术的级联是否有可能发生?
7.假设你是一家公司的HR,现在部门领导要求你解释一个近期的招聘错误决定。公司面试两个候选人 A 和 B ,他们竞争同一个岗位。所有的HR全部参加面试并一起决定聘用哪一个人,每一个HR都希望选择一个最合适人选,然而面试之后,每个HR对两个人谁是最佳选择有不同看法。做最终决定时,每个HR宣布自己认为的两个候选人中的最佳人选。结果是,每个人都认为候选人 A 最合适,因为没有再进行讨论,便决定录用 A 。现在 A 工作了一段时间之后,大家又开始觉得实际上录用 B 是最好的选择:
1)老板确信在开会之前,至少有一些HR认为候选人 B 是最佳人选,那么为什么开会时大家一致支持候选人 A 。你如何向老板解释这一原因?
2)你能否设计另一种机制,使得委员会成员可以透露对候选人的初步不同意见,并且也能够让候选人 B 得到这份工作的机会更大一些。
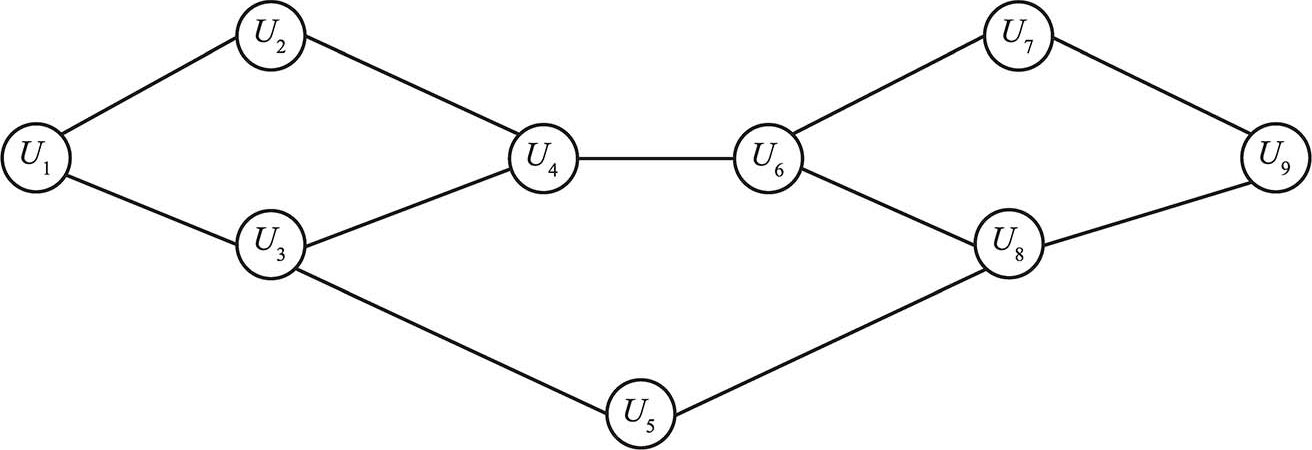
图1-21 第8题图
8.考虑如图1-21所示的网络,假设每个节点开始采用行为 B ,每个节点转而采取行为 A 的门槛值为 q =1/2:
1)设节点 U 1 和 U 4 组成一个行为 A 的初用节点集 S ,如果其他节点遵循门槛规则选择行为,那么哪些节点最终会转向行为 A ?
2)在图1-21中的 S 之外找出一个密度大于1- q =1/2的聚簇,当行为 A 以 S 为开始集合, q 为门槛值时,这个聚簇阻碍 A 传播到所有其他节点。
9.考虑如图1-22所示的社会网络,假设每个节点开始采用行为 B ,每个节点转而采取行为 A 的门槛值为 q =2/5:
1)设节点 U 1 和 U 2 组成一个行为 A 的初用节点集 S ,如果其他节点遵循门槛规则选择行为,那么哪些节点最终会转向行为 A ?简要解释即可。
2)求不包含 S 密度大于1- q =3/5的聚簇,它能阻止行为 A 传播到所有节点,设该过程从 S 开始且门槛值为 q 。
3)假设允许在指定的网络中添加一个边,从节点 U 1 或 U 2 连接到任何一个当前未连接的节点。是否存在这样一种连接方式,使得以初用节点集 S 开始,门槛值为2/5,最终行为 A 将传播到所有节点?
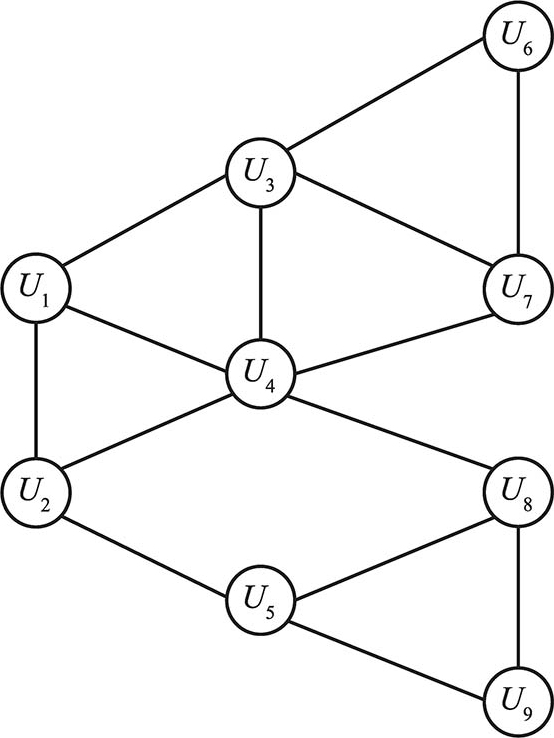
图1-22 第9题图
10.考虑1.2.1节中介绍的协调博弈模型,如果节点 v 和 w 都试图决定是选择行为 A 还是 B ,则:如果 v 和 w 都选择行为 A ,它们分别得到收益 a >0;如果它们都采用 B ,则分别获得收益 b >0;如果它们采取相反的行为,分别获得收益0;并且任何一个节点的总收益取决于该节点与每个邻居进行这种协调博弈得到的收益和。现在考虑一个更一般化的模型,当节点与邻居节点采取不同的行为时,得到的收益不为0,而是一些小的正数 x ,即 如果与邻居节点采取相反的行为,它们分别得到收益 x ,其中 x 是一个小于 a 和 b 的正数 。那么在该模型变体中,每个节点的决策是否依然基于门槛规则?具体来说,是否可以形成一个以变量 a 、 b 、 x 形式表达的临界值 q 的公式,且如果每个节点 v 至少有比例为 q 的邻居采用 A ,也会采用行为 A ,否则将采用 B ?
[1] PATTERSON G R,FORGATCH M S,DEGARMO D S.Cascading effects following intervention[J].Development and psychopathology,2010,22(4):949-970.
[2] BANERJEE A V.A simple model of herd behavior[J].The quarterly journal of economics,1992,107(3):797-817.
[3] AJRALDI V,PITTAVINO M,VENTURINO E.Modeling herd behavior in population systems[J].Nonlinear Analysis:Real World Applications,2011,12(4):2319-2338.
[4] MORRIS W N,MILLER R S.The effects of consensus-breaking and consensus-preempting partners on reduction of conformity[J].Journal of Experimental Social Psychology,1975,11(3):215-223.
[5] ASCH S E.Opinions and social pressure[J].Scientific American,1955,193(5):31-35.
[6] MILGRAM S.Behavioral study of obedience[J].The Journal of abnormal and social psychology,1963,67(4):371.
[7] LESKOVEC J,ADAMIC L A,HUBERMAN B A.The dynamics of viral marketing[J].ACM Transactions on the Web (TWEB),2007,1(1):5-es.
[8] HO J Y C,DEMPSEY M.Viral marketing:Motivations to forward online content[J].Journal of Business research,2010,63(9-10):1000-1006.
[9] BOEHMER J,TANDOC E C.Why we retweet:Factors influencing intentions to share sport news on Twitter[J].International Journal of Sport Communication,2015,8(2):212-232.
[10] DUAN W,GU B,WHINSTON A B.Informational cascades and software adoption on the internet:an empirical investigation[J].MIS quarterly,2009:23-48.
[11] SUROWIECKI J.The wisdom of crowds[M].New York:Anchor,2005.
[12] WELCH I.Sequential sales,learning,and cascades[J].The Journal of finance,1992,47(2):695-732.
[13] EFTEKHAR M,GANJALI Y,KOUDAS N.Information cascade at group scale[C]//Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining.2013:401-409.
[14] MILGRAM S,BICKMAN L,BERKOWITZ L.Note on the drawing power of crowds of different size[J].Journal of Personality and Social Psychology,1969,13(2):79-82.
[15] MULLEN B,COPPER C,DRISKELL J E.Jaywalking as a function of model behavior[J].Personality and Social Psychology Bulletin,1990,16:320-330.
[16] WALKER M,HARRIMAN S,COSTELLO S.The influence of appearance on compliance with a request[J].The Journal of Social Psychology,1980,112(1):159-160.
[17] BIKHCHANDANI S,HIRSHLEIFER D,WELCH I.A theory of fads,fashion,custom,and cultural change as informational cascades[J].Journal of political Economy,1992,100(5):992-1026.
[18] HUCK S,OECHSSLER J.Informational cascades in the laboratory:Do they occur for the right reasons[J].Journal of Economic Psychology,2000,21(6):661-671.
[19] CELEN B,KARIV S.Distinguishing informational cascades from herd behavior in the laboratory[J].American Economic Review,2004,94(3):484-498.
[20] LEWIN K.Group decision and social change[J].Readings in social psychology,1947,3(1):197-211.
[21] MORRIS S.Contagion[J].The Review of Economic Studies,2000,67(1):57-78.
[22] EASLEY D,KLEINBERG J.Networks,Crowds,and Markets:Reasoning About a Highly Connected World[M].Cambridge:Cambridge University Press,2010.
[23] GRANOVETTER M.Threshold models of collective behavior[J].American journal of sociology,1978,83(6):1420-1443.
[24] KEMPE D,KLEINBERG J,TARDOS É.Maximizing the spread of influence through a social network[C]//Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining.2003:137-146.
[25] STAUFFER D,AHARON A.Introduction to percolation theory[M].Florida:CRC Press,2018.
[26] BROADBENT S R,HAMMERSLEY J M.Percolation processes:I.Crystals and mazes.Mathematical proceedings of the Cambridge philosophical society[M].Cambridge:Cambridge University Press,1957,53(3):629-641.
[27] GRIMMETT G R,MARSTRAND J M.The supercritical phase of percolation is well behaved[C]// Proceedings of the Royal Society of London.Series A:Mathematical and Physical Sciences,1990,430(1879):439-457.
[28] 李明,汪秉宏.逾渗模型与复杂网络[J].现代物理知识,2015,027(003):32-37.
[29] MOORE C,NEWMAN M E J.Exact solution of site and bond percolation on small-world networks[J].Physical Review E,2000,62(5):7059.
[30] 梅淳惠.逾渗模型的蒙特卡罗模拟[J].南京邮电大学,2016.
[31] PRINZ G A.Magnetoelectronics[J].Science,1998,282(5394):1660-1663.
[32] CHRISTENSEN K.Percolation theory[J].Imperial College London,2002:1-40.
[33] CHALUPA J,LEATH P L,REICH G R.Bootstrap percolation on a Bethe lattice[J].Journal of Physics C:Solid State Physics,1979,12(1):L31.
[34] ADLER J.Bootstrap percolation[J].Physica A:Statistical Mechanics and its Applications,1991,171(3):453-470.
[35] JENSEN I.Size and area of square lattice polygons[J].Journal of Physics A:Mathematical and General,2000,33(18):3533.
[36] HENKEL M,HINRICHSEN H,LÜBECK S,et al.Directed Percolation[C]//Non-Equilibrium Phase Transitions.Theoretical and Mathematical Physics,2008:59-100.
[37] HAMMERSLEY J M,WELSH D J A.First-passage percolation,subadditive processes,stochastic networks,and generalized renewal theory[J].Springer,1965:61-110.
[38] ACHLIOPTAS D,D'SOUZA R M,SPENCER J.Explosive percolation in random networks[J].Science,2009,323(5920):1453-1455.
[39] RADICCHI F,FORTUNATO S.Explosive percolation:A numerical analysis[J].Physical Review E,2010,81(3):036110.
[40] ERDÖS P,RÉNYI A.On the evolution of random graphs[J].Publ Math Inst Hung Acad Sci,1960,5(1):17-60.
[41] BARABÁSI A L,BONABEAU E.Scale-free networks[J].Scientific american,2003,288(5):60-69.
[42] CALLAWAY D S,NEWMAN M E J,STROGATZ S H,et al.Network robustness and fragility:Percolation on random graphs[J].Physical review letters,2000,85(25):5468.
[43] DEL FERRARO G,MORENO A,MIN B,et al.Finding influential nodes for integration in brain networks using optimal percolation theory[J].Nature communications,2018,9(1):1-12.
[44] RADICCHI F,CASTELLANO C.Breaking of the site-bond percolation universality in networks[J].Nature communications,2015,6(1):1-7.
[45] CHANG K C,ODAGAKI T.Site-bond percolation problems[J].Journal of statistical physics,1984,35(5):507-516.
随着现代社会的高速发展,全球人口流动更加频繁,互联网用户规模迅速上升,社交媒体平台发展壮大,社会中的相互关系越发复杂。例如描述社会关系的朋友网络、描述协作关系的合作网络、描述金钱流动的金融网络、描述疾病传播的生物网络等。如何对现实世界中多种多样的网络进行抽象建模,从理论模型的角度对网络特性进行刻画,一直是计算社会学研究的核心问题之一。为了描述网络交互的随机性,20世纪50年代,Erdos和Renyi提出了ER随机网络模型 [1] ,这是一类按概率生成交互关系的模型,从数学上开创了复杂网络理论的系统性研究 [2] 。在此基础上,后人对随机网络进行了一系列的拓展,如P1随机网络模型 [3] 、P2随机网络模型 [4] 、指数随机网络模型 [5] 等。