




总体而言,汽车是一个多自由度的振动系统,车辆悬架系统的关键组件——阻尼减振器,对汽车振动性能的改善起到了至关重要的作用。
在静平衡位置(弹簧力与阻尼力的合力抵消了车身的重力),如果将汽车车身整体简化为一个质量块,则车身重量由一个单独的阻尼减振器支撑,此时汽车可视为一个单自由度振动系统,如图2-1所示。
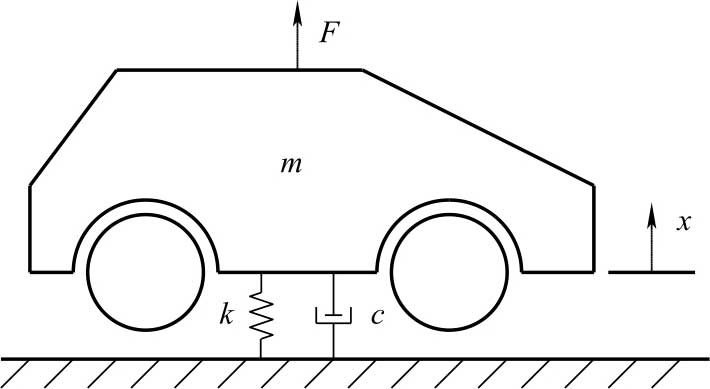
图2-1 汽车单自由度振动系统
m —汽车车身质量(kg) k —汽车悬架弹簧刚度(N·m -1 ) c —汽车悬架阻尼系数(N·s·m -1 )
F —外界施加的力(N) x —车身相对于静平衡位置的时变位移(m)
假设汽车前后悬架结构相同并且左右对称,汽车四个车轮受到同样的外界激励,取1/4汽车作为研究对象,将汽车抽象为一个单独质量块的上下往复振动系统,则可以建立如图2-2所示的动力学模型。
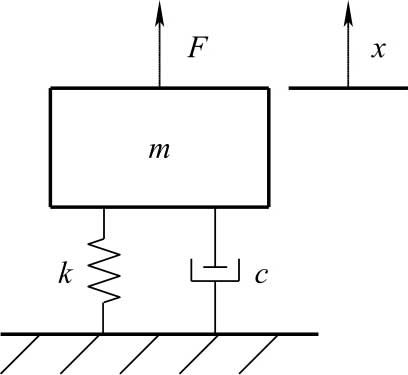
图2-2 汽车单自由度振动动力学模型
取车身静平衡位置为坐标原点,分析其受力可得到如图2-3所示的受力示意图。
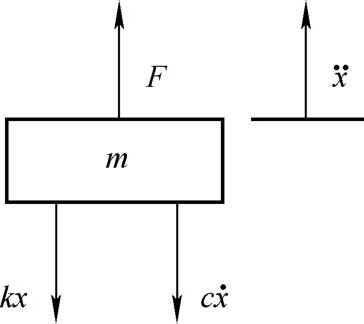
图2-3 四分之一车辆单自由度模型示意图
根据牛顿第二定律,可以得到该振动模型的动力学方程为

或者写成
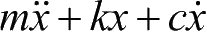 =
F
。
=
F
。
如图2-4所示的振动系统,弹簧和阻尼器垂直放置,系统受到重力的影响,弹簧被压缩或伸长,其静变形量 δ st 为

式中, g 为重力加速度。
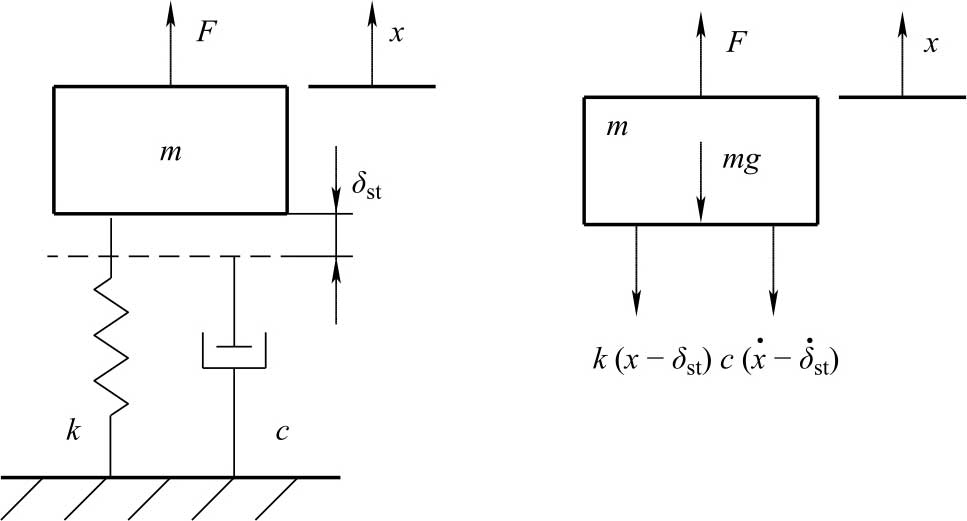
图2-4 四分之一车辆振动模型静平衡示意图
对图2-4所示的四分之一车辆振动模型,根据牛顿第二定律可得
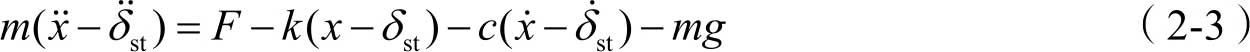
式中,
x
是从弹簧末端的静变形位置计算的位移。当
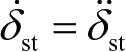 =0,式(2-3)可简化为式(2-1)所表示的运动方程,说明质量块的重力对系统的运动方程没有影响。
=0,式(2-3)可简化为式(2-1)所表示的运动方程,说明质量块的重力对系统的运动方程没有影响。
式(2-3)是一个二阶非齐次线性微分方程,根据高等数学中二阶非齐次线性微分方程的求解方法进行求解。下面通过一个算例给出线性微分方程的求解方法。
[例2-1] 求解如下微分方程:

显然,该方程是一个一阶常系数齐次线性方程,可以利用数学的相关方法求解其通解,具体计算过程如下:
1)分离变量

2)两边积分

3)化简

4)计算得

5)将已知 x (0)=10代入式(2-8)可得

6)可得该一阶常系数齐次线性方程的特解为

7)利用MATLAB绘制该通解的曲线,在MATLAB编辑器中运行如下代码:

8)可以得到如图2-5所示的仿真曲线。
在Simulink中搭建模型求解方程(2-4)方法如下:
1)新建一个Simulink文件。
2)从Library Browser模块中添加一个Integrator积分模块,设定初始值为10。
3)从Library Browser模块中添加一个Gain增益模块,设定增益值为-1。
4)从Library Browser模块中添加一个Scope示波器模块。
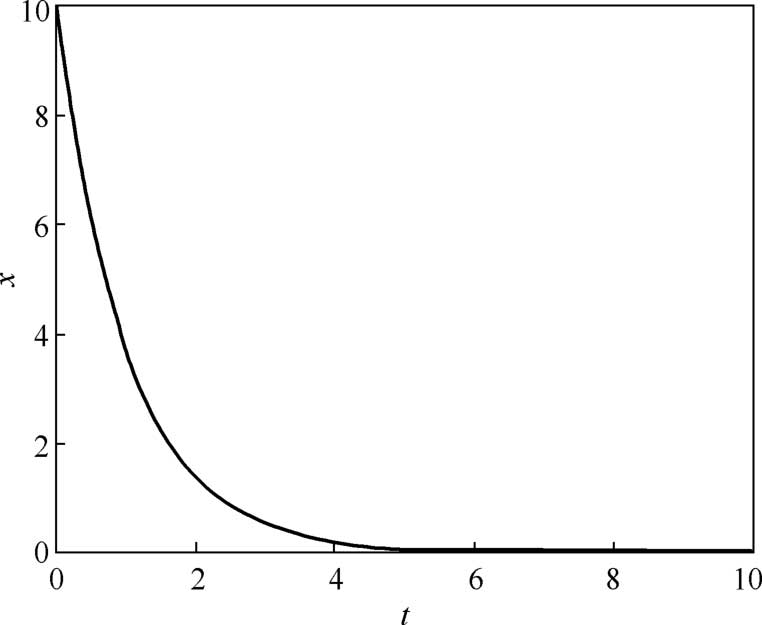
图2-5 一阶常系数齐次线性方程数值解的仿真曲线
5)将各个模块进行连接,如图2-6所示。
6)单击SIMULATE选项中的“Run”按钮,运行该仿真模型。
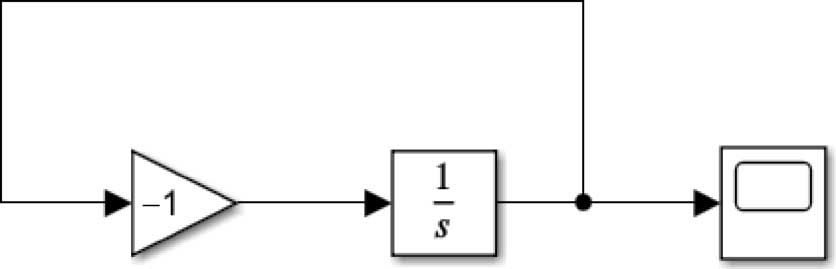
图2-6 一阶常系数齐次线性方程的Simulink模型
7)双击示波器模块查看该一阶常系数齐次线性方程的输出结果。
仿真结果分析:从图2-5和图2-7可以看出,该一阶常系数齐次线性微分方程的解是一条不断衰减的曲线,通过手动计算得到的数值解和利用Simulink模块计算得到的解是一致的。
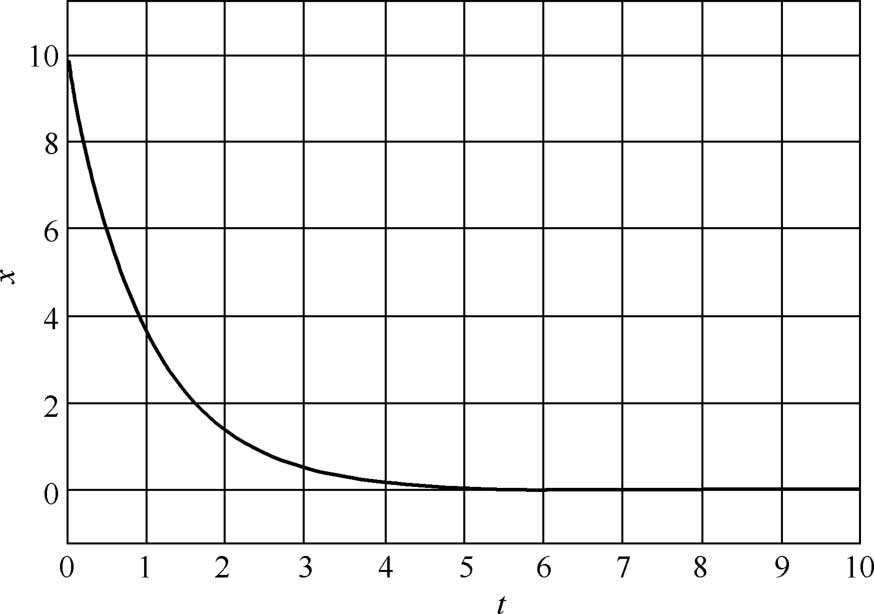
图2-7 一阶常系数齐次线性方程在Simulink中的解
[例2-2] 求解如下微分方程:
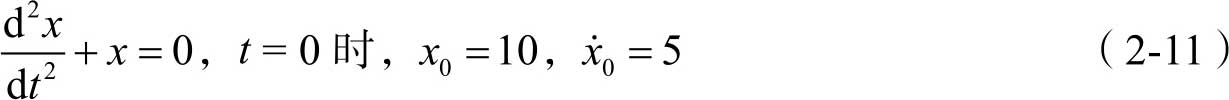
该方程是一个二阶常系数齐次线性方程。根据特征方程根的不同,二阶常系数齐次线性方程的通解可以分为以下三种形式,见表2-1。
表2-1 二阶常系数齐次线性方程的通解形式

具体计算过程如下:
1)根据所给的微分方程写出对应的特征方程

2)求特征方程的根,得到一对共轭复根

3)根据表2-1,可得该微分方程的通解和其一阶导数

4)代入已知条件
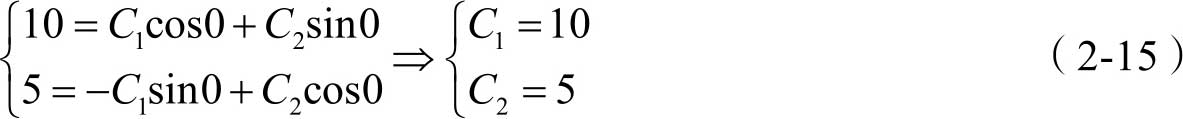
5)求得该微分方程的特解为

6)利用MATLAB绘制该通解的曲线,在MATLAB编辑器中运行如下算法:

7)可以得到仿真曲线如图2-8所示。
在Simulink中搭建模型求解方法如下:
1)新建一个Simulink文件。
2)从Library Browser模块中添加两个积分模块,第一次积分的初始值设置为5,第二次积分的初始值设置10。
3)从Library Browser模块中添加一个增益模块,设定增益值为-1。
4)从Library Browser模块中添加一个示波器模块。
5)将各个模块进行连接,如图2-9所示。
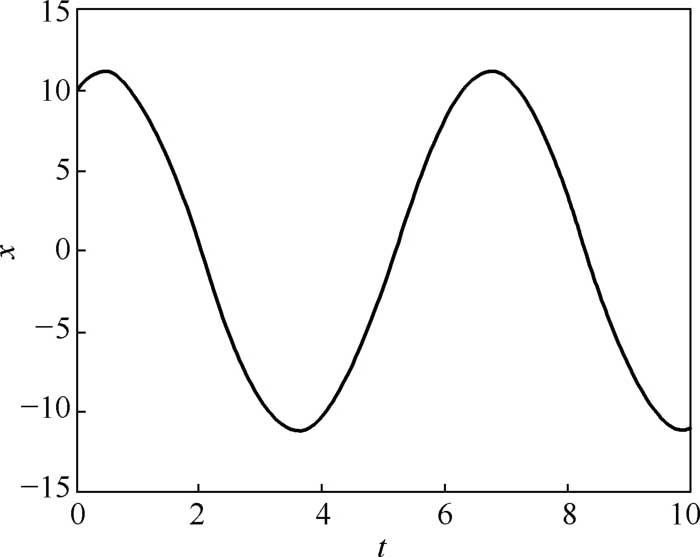
图2-8 二阶常系数齐次线性方程的数值解
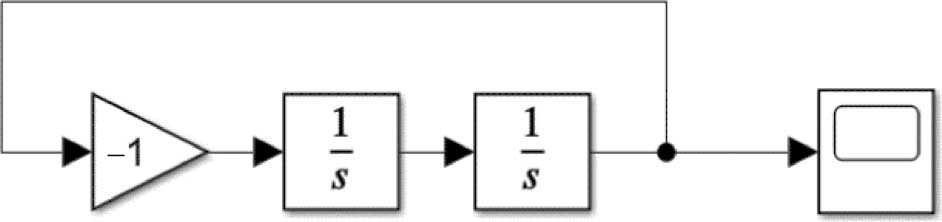
图2-9 二阶常系数齐次线性方程的Simulink模型
6)单击“Run”按钮,运行该仿真模型。
7)双击示波器模块,查看该二阶常系数齐次线性方程的输出结果(图2-10)。
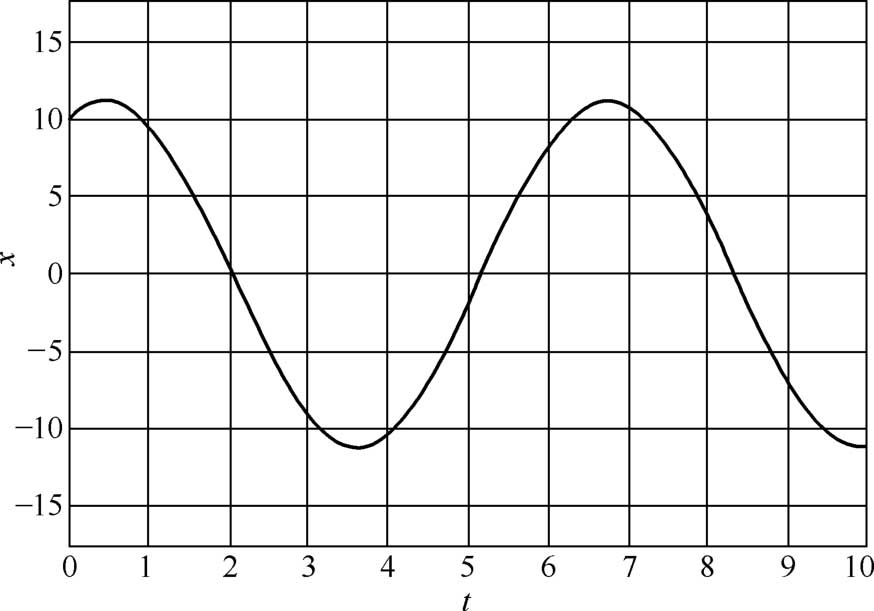
图2-10 二阶常系数齐次线性方程在Simulink中的解
仿真结果分析:从图2-8和图2-10可以看出,该二阶常系数齐次线性方程的解是一条周期和振幅都保持不变的简谐运动曲线。通过手动计算得到的数值解和利用Simulink模块计算得到的解是相同的曲线。