




Mallat最早提出了基于小波变换模极大值的边缘检测基本思想,把图像处理中小波变换的应用提高到了一个新的层次。
首先定义二维平滑函数,并将其水平和垂直方向的一阶偏导数作为用于图像变换的两个基本小波,然后将两个基本小波的伸缩小波与图像的卷积分别定义为小波变换的水平和垂直分量,并根据此求出小波变换的模和辐角,把图像边缘定义为沿相角方向的小波变换模极大值,建立二维小波变换模极大值与图像边缘点之间的对应关系。
设二维平滑函数 θ ( u , v )满足
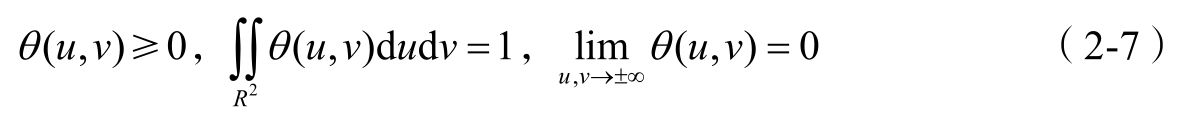
记

设 f ( u , v )表示一幅连续的图像,则对任意的 f ( u , v )∈ L 2 ( R 2 ),( f * θ s )( u , v )表示 f ( u , v )经 θ s ( u , v )平滑后的图像,其中 s >0为平滑的尺度。
由 θ ( u , v )定义两个二维小波为

记
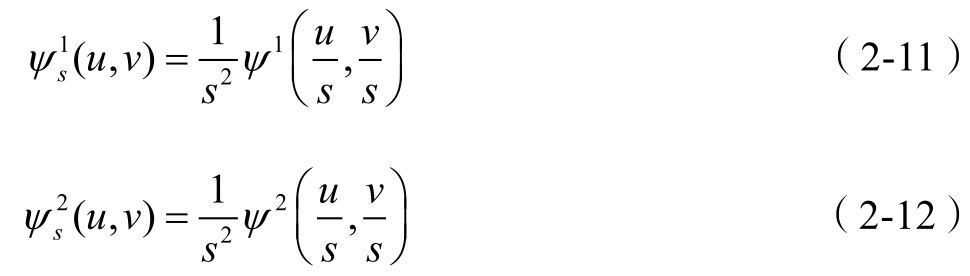
则 f ( u , v )在尺度 s 上的二维小波变换为
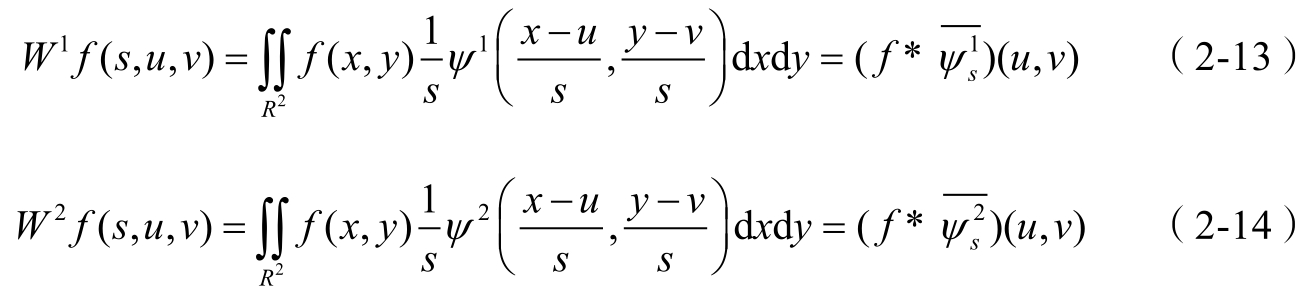
其中,
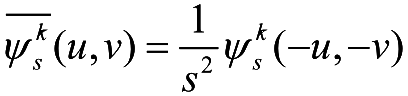 ,
k=
1,2。
,
k=
1,2。
对于小波变换的两个分量 W 1 f ( s , u , v )和 W 2 f ( s , u , v ),容易证明:
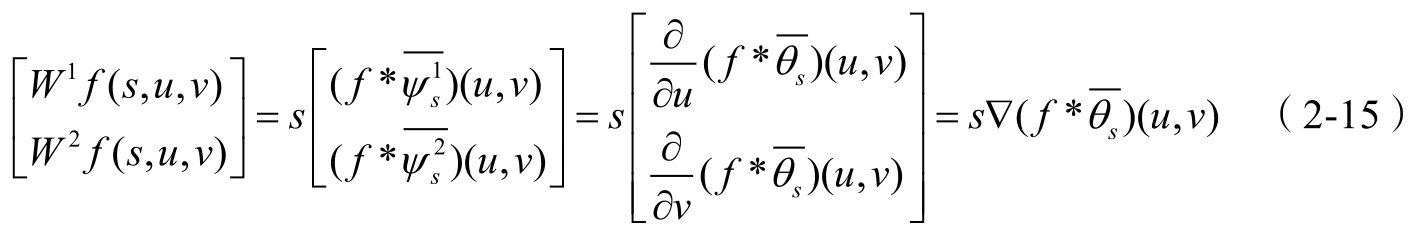
因而,
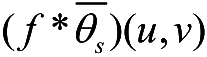 的梯度向量
的梯度向量
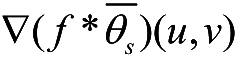 的模与小波变换的模成比例,即
的模与小波变换的模成比例,即
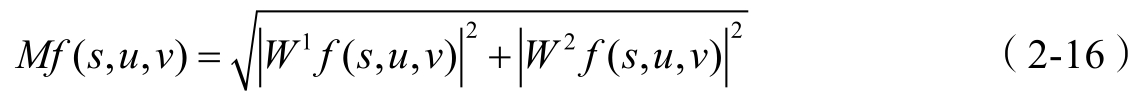
梯度方向与水平方向 u 的夹角(幅角或相角)为
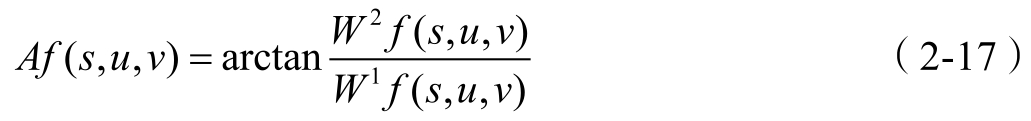
于是,计算一个光滑函数
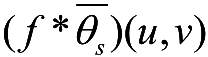 沿着梯度方向的模极大值等价于计算小波变换的模极大值。记
沿着梯度方向的模极大值等价于计算小波变换的模极大值。记
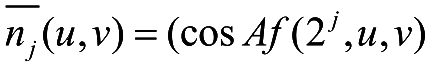 ,sin
Af
(2
j
,
u
,
v
)),则单位向量
,sin
Af
(2
j
,
u
,
v
)),则单位向量
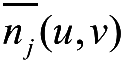 与梯度向量
与梯度向量
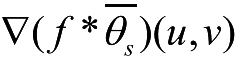 是平行的。因此,在尺度
s
下,若模
Mf
(
s
,
u
,
v
)在点(
u
1
,
v
1
)沿着(
u
,
v
)
=
(
u
1
,
v
1
)
+λ∇f
(
u
1
,
v
1
)方向,当|
λ
|充分小时取到局部极大值,则点(
u
1
,
v
1
)就是
是平行的。因此,在尺度
s
下,若模
Mf
(
s
,
u
,
v
)在点(
u
1
,
v
1
)沿着(
u
,
v
)
=
(
u
1
,
v
1
)
+λ∇f
(
u
1
,
v
1
)方向,当|
λ
|充分小时取到局部极大值,则点(
u
1
,
v
1
)就是
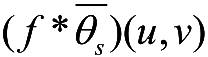 的一个边缘点,即
f
(
u
,
v
)的一个突变点。而边界的方向与
的一个边缘点,即
f
(
u
,
v
)的一个突变点。而边界的方向与
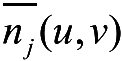 垂直。这表明,通过检测二维小波变换的模极大值点可以确定图像的边缘点。
垂直。这表明,通过检测二维小波变换的模极大值点可以确定图像的边缘点。
边缘定义为小波变换模取极值之处,其方向则沿着与幅角垂直的方向。但是噪声也是灰度突变点,也是极大值点。因为小波变换具有使信号能量集中、噪声能量分散的性能,还能将信号能量集中在少数小波系数上,所以边缘的小波系数幅值比较大,而噪声能量比较分散,小波系数幅值较小。所以用平滑函数的一阶导数作为小波函数对图像进行小波变换,在一个尺度下大于一定阈值的小波系数的模极大值点即对应图像的边缘点,综合大尺度下好的抗噪性和小尺度下好的定位性提取出边缘,这就是小波变换用于边缘检测的原理。
设数字图像 D 有 N × N 个像素,即 D= { d n , m | n , m= 0,1,…, N -1},利用小波变换模极大值对数字图像进行边缘检测的算法如下:
1)选定平滑函数 θ ( x , y )为尺度函数,求出 θ ( x , y )的一阶偏导数 ψ x ( x , y )和 ψ y ( x , y ),并将其作为小波函数;对图像进行小波变换,在尺度 s= 2 j 下,计算数字图像 D 在每一点( n , m )的二维小波变换 W 1 f (2 j , n , m )和 W 2 f (2 j , n , m ), n , m= 0,1,…, N -1,1≤ j ≤ J= log 2 N 。分解的尺度数可根据需要而定。两个方向的小波系数相当于采用小波变换进行图像分解时的水平细节系数和垂直细节系数。
2)由各个点小波系数计算每一点的幅值 Mf (2 j , n , m )和幅角的正切值tan Af (2 j , n , m )。从数字图像的结构图2-4a可知,每个像素点的周围只有8个邻接点,这些邻接点将平面分成8个区域,如图2-4b所示,考虑到梯度方向的对称性,只需考虑1~4区域中的梯度方向,这些区域的每个像素点的梯度方向必落入下面4个区间之一:
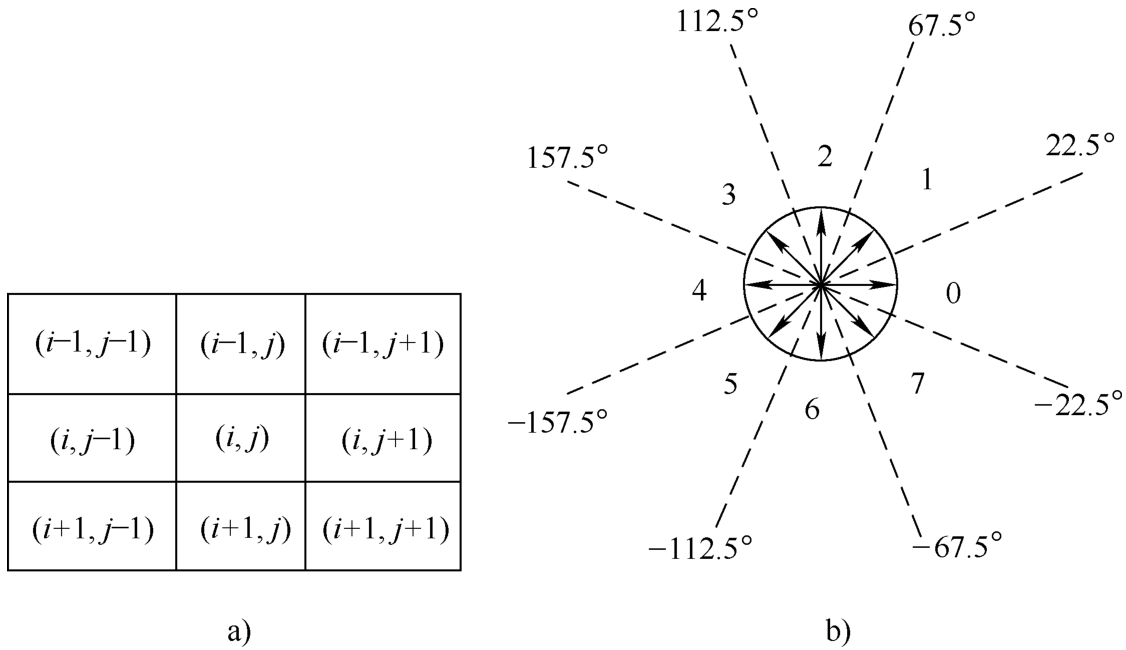
图2-4 8邻域像素
a)数字图像的邻域结构 b)邻接点划分的8个区域
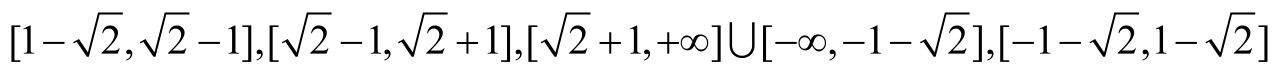
3)按照梯度伸展方向比较临近的前后两个点的幅值,取模最大的点作为候选边缘点。对每个像素点( n , m ),幅值和幅角为
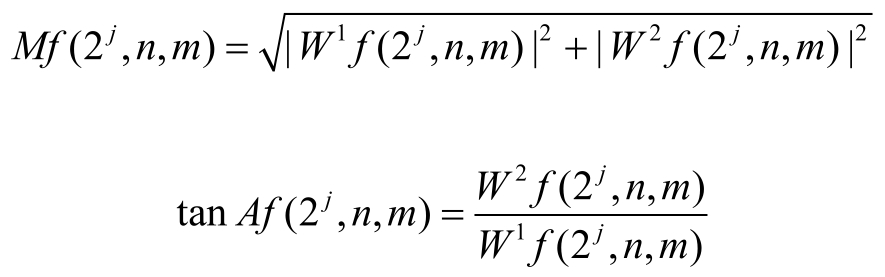
4)求边界点。由于噪声的存在,需要进行模极大值点阈值化处理,即对小波变换系数模局部极大值设定阈值,阈值根据小波变换整体的模值统计直方图确定:
T > 0,对于 n , m= 0,1,…, N -1,如果 Mf (2 j , n , m )≥ T , Mf (2 j , n , m )取得局部极大值,即( n , m )为模极大值点,则( n , m )是一个边界点。
5)在各尺度上连接边界点,形成各尺度下沿着边界的极大曲线。
图像中边界点一般形成一条曲线,而该曲线通常是某些重要结构的边界。将各个小波模极大点连接起来,就形成一条沿着边界的极大曲线。在离散情况下,极大曲线是通过将图像离散采样点中两个相邻的边界点( n , m )与( n , m ) +γ ( n , m )连接起来形成的,其中 γ ( n , m )垂直于扇区Code Af (2 j , n , m )对应的梯度方向。多尺度边缘提取算法流程如图2-5所示。
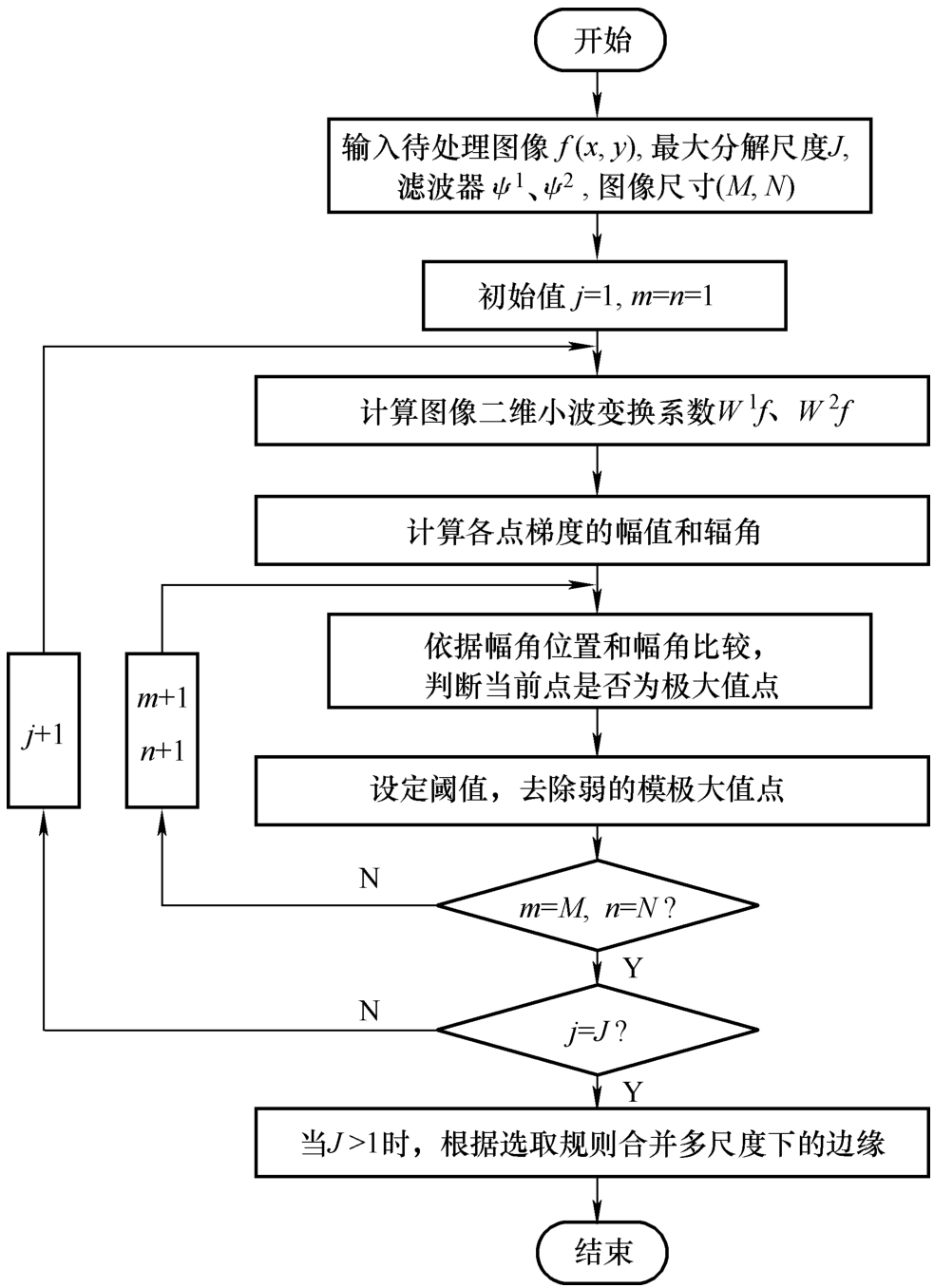
图2-5 多尺度边缘提取算法流程
实验采用一张打上激光束的零件图片,对图像进行滤波去噪、增强等预处理后,分别采用小波变换模极大值多尺度边缘检测算法和传统的Roberts算子对图像边缘信息进行检测,结果如图2-6所示。从图中可以看到,传统的Roberts算子检测的边缘不准确,且把图像中的一些信息误认为边缘检测出来,检测效果不如小波变换模极大值多尺度边缘检测算法。

图2-6 灰度图及小波变换边缘图
a)灰度图 b)垂直方向小波变换 c)水平方向小波变换 d)小波变换模 e)小波变换零件边缘图 f)由Roberts算子检测的边缘图