




1.将一枚硬币连续抛两次,以 X 表示所抛两次中出现正面的次数,试写出 X 的分布律.
2.设随机变量
X
的概率分布为
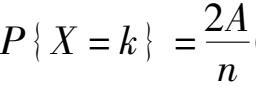 (
k
= 1,2,…,
n
),试确定常数
A.
(
k
= 1,2,…,
n
),试确定常数
A.
3.若 X 服从 0-1 分布,且 P { X = 1}= 2 P { X = 2},求 X 的概率分布.
4.设 X 服从泊松分布,且已知 P { X = 1}= P { X = 2},求 P { X = 4}.
5.自动生产线在调整之后出现废品的概率为 p ,当在生产过程中出现废品时立即重新进行调整,求在两次调整之间生产的合格品数 X 的概率分布.
6.某射手有 5 发子弹,射一次命中的概率为 0.8,如果命中了就停止射击,如果不命中就一直射到子弹用尽,求射击次数 X 的概率分布.
7.设随机变量 X 的分布律见表 2.10.
表 2.10

试求
(1) X 的分布函数.
(2) P { X ≤1.5}与 P {0 < X ≤3.8}.
8.某种型号的电子管寿命 X (小时)作为一随机变量,其概率密度函数为
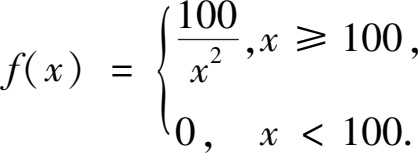
(1)求 X 的分布函数.
(2)若一无线电器材配有三个这样的电子管,试计算该无线电器材使用 150 小时内不需要更换电子管的概率.
9.已知随机变量 X 的概率密度函数为
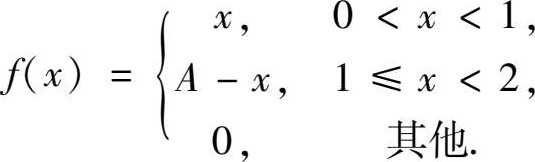
(1)确定常数 A.
(2)求 X 的分布函数 F ( x ).
(3)求 P { X < 0.5}.
10.设 X 的分布函数为
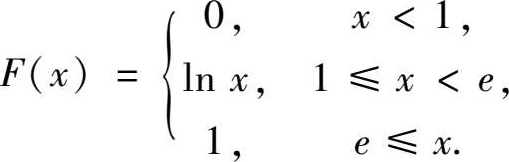
试求(1) P { X ≤2}, P {0 < X ≤3}.(2)概率密度函数 f ( x ).
11.设随机变量 X 的分布函数为
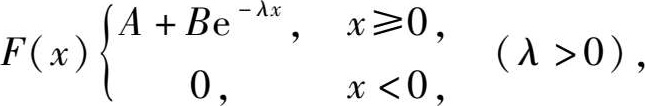
求:(1)常数 A , B ;
(2) P { X ≤2}, P { X > 3};
(3)概率密度 f ( x ).
12.设 X ~ N (0,1),试求下列概率: P { X ≤1.64}, P { X ≥ -0.83}, P { X ≥2}.
13.设 X ~ N (10,2 2 ),试求下列概率: P { X ≤10}, P {8 < X ≤14}, P { X ≥8}.
14.一工厂生产的电子管的寿命 X (以小时计)服从参数为 μ = 160 的正态分布,若要求 P {120 < X ≤200}≥0.8,允许 σ 最大为多少?
15.已知 X 服从区间[2,5]上的均匀分布,现在对 X 进行三次独立观测,试求至少有两次观测值大于 3 概率.
16.设随机变量 X 的分布律如下表所示,求 Y = 2 X 2 + 1 的分布律.
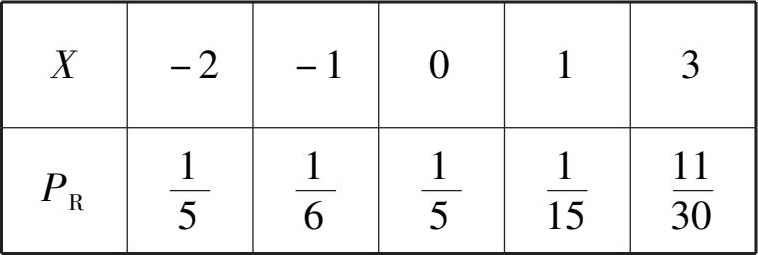
17.已知连续型随机变量 X 的概率密度函数为
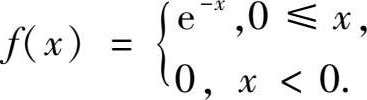
求 Y = X 2 的概率密度函数.
18.已知连续型随机变量
X
的概率密度函数为
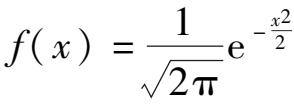 ,-∞ <
x
< + ∞ ,求
Y
=
,-∞ <
x
< + ∞ ,求
Y
=
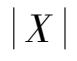 的概率密度函数.
的概率密度函数.

二维码 2.6
习题 2 答案