




线性回归针对的问题是其输出的结果为连续性变量。针对分类问题,其输出的结果为离散变量,所以无法直接使用线性回归的办法。例如,一个典型的回归问题,给定一组数据
( x 1 ,y 1 ),( x 2 ,y 2 ),···,( x n ,y n )
其中
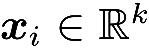 ,但
y
i
∈{-1,1}为两个点的离散变量。如何选取函数空间以及损失函数成为解决问题的核心。首先来看损失函数,因为
y
i
取值为离散型,所以不能使用
,但
y
i
∈{-1,1}为两个点的离散变量。如何选取函数空间以及损失函数成为解决问题的核心。首先来看损失函数,因为
y
i
取值为离散型,所以不能使用
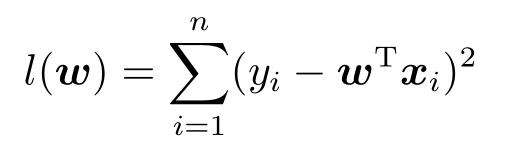
接下来采用概率论的思维研究这个问题。假设对于两个随机变量( X,Y ),它们之间有联合分布 p ( x,y ),其中 Y 取值两个点。给出独立随机抽样的样本
( x 1 ,y 1 ),( x 2 ,y 2 ),···,( x n ,y n )
试计算条件概率分布函数 p ( y | x )。从条件概率的公式可知,这等价于计算 p ( y =0| x ) ,p ( y =1| x )两个函数。如果令
f ( x )= p ( y =0| x )
则当 y =1时,有
1- f ( x )= p ( y =1| x )
使用一个关于 x 的函数来判别 y 的取值,可以看成是一个判别模型。这点有别于后面会讲到的生成模型。显然,满足这样条件的函数应满足0≤ f ( x )≤1,另外,足够光滑的函数应该使得应用更加方便。为此,假设一个函数形式兼顾线性以及作为概率分布函数介于0∼1且足够光滑的约束。考虑一个把实数映射到(0,1)之间的函数
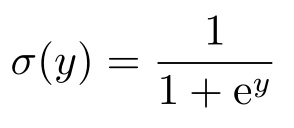
复合上一个线性函数 y = w T x + b ,就有
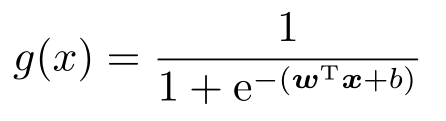
这个函数可以看成一个概率
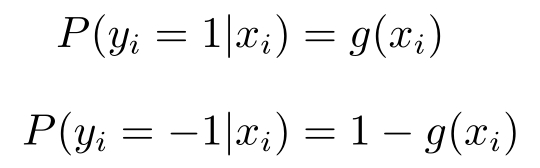
为了简化记号,还是采取升维的方法,那么就可以省略 b ,从而写成
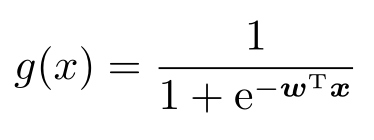
这样,所有样本的密度函数就是
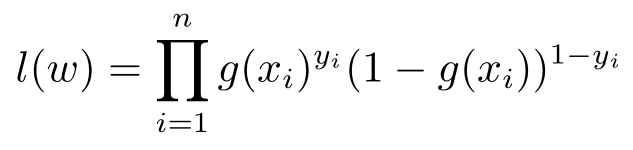
再一次应用极大似然估计的想法,使得希望求解
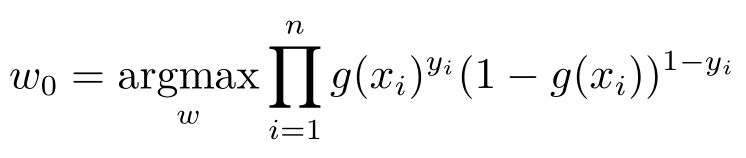
或者在定义损失函数为- l ( w )以后,化为极小化损失函数的问题。对上述问题求解,首先可以用对数函数做变换,即
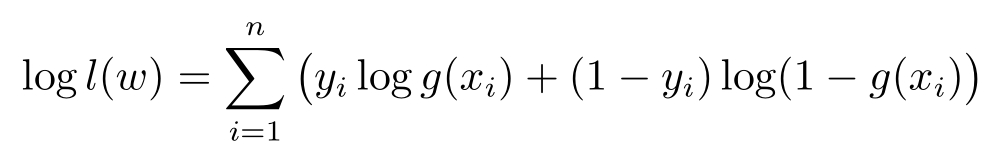
但是,这个函数的极值是没有办法用闭形式解来给出的,所以只能求助于数值方法。这个函数表达不是 w 的一次函数,从而不可能使用线性规划方法求解,也不是二次函数,所以也不可能使用二次规划方法求解,但是可以使用梯度下降法来求解这个优化问题。
另外,既然让 Y 取值为{-1,1},同时定义
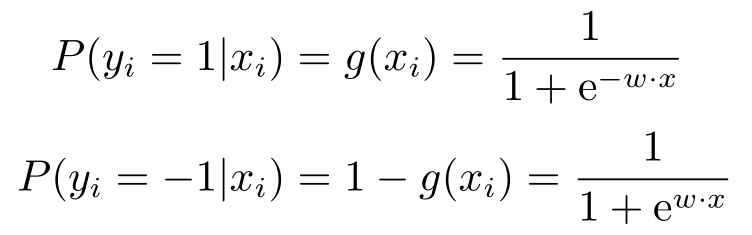
对于这个特殊形式的函数,有
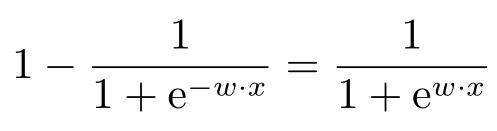
所以当 y i 取{-1,1}时,也可以看成目标是
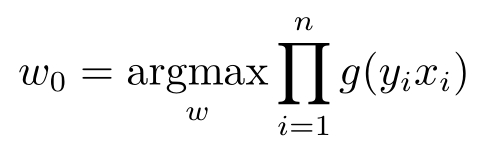
线性回归和逻辑回归都是使用线性的函数作为假设函数。线性回归有简单闭形式的解,但是逻辑回归没有简单闭形式的解,所以必须使用数值方法解答。最简单的数值方法就是梯度下降法,该方法在以后会进行介绍。重点是这里有待优化的损失函数是个凸函数,所以最小值存在并且唯一,并不会有神经网络常见的局部极小值的情况。
当得到了 f ( x )= P ( y | x )以后,该如何分类呢?直观的办法是,如果 f ( x )>0.5,则分类 y =1,但是有1- f ( x )的概率为 y =-1。下面进行更严格的证明。
假设正确的概率函数是 f ( x ),即
P ( y =1| x )= f ( x )
定义
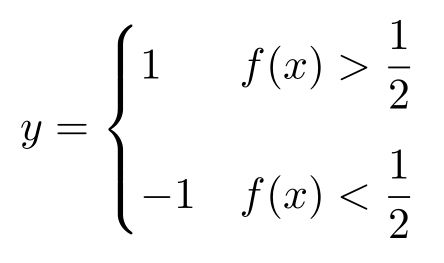
显然对于这个分类方法,如果 f ( x )>0.5,则分类 y =1,但是有1- f ( x )的概率为 y =0,从而错误率是1- f ( x )。反之,如果 f ( x )<0.5,则判断 y =-1,但是有 f ( x )的概率为 y =1。所以,无论 f ( x )是多少,错误率都是
min( f ( x ),1- f ( x ))
现在,如果有任何一个关于 x 的分类函数,根据函数判断 y =-1时,总有 f ( x )的可能性为 y =1,同理,当判断 y =1时,总有1- f ( x )的可能性为 y =-1。所以,无论分类函数是多少,错误率不是 f ( x )就是1- f ( x )。显然,这样的错误率比起min( f ( x ),1- f ( x ))来得大,因此上述判断是最优的。